Додаток 2

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Національний технічний університет України

«Київський політехнічний інститут»

Кафедра динаміки, міцності машин і опору матеріалів

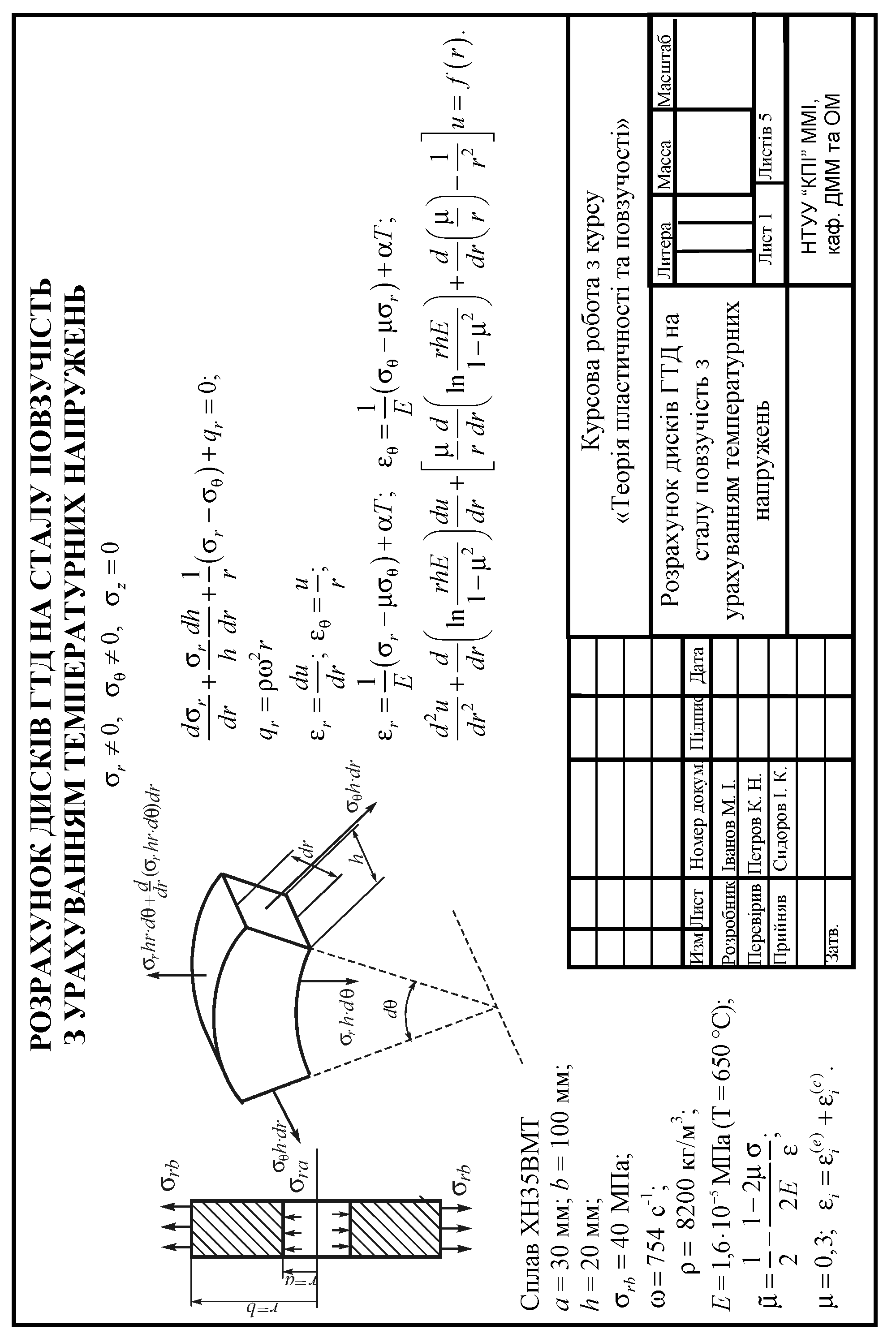
КУРСОВА РОБОТА

з дисципліни «Теорія пластичності та повзучості»

Тема

Керівник Виконав

Допущений до захисту студент курсу

„ ” 200 р. групи

Захищено з оцінкою залікова книжка

№

2003

Додаток 3

Додаток 4

Текст комп’ютерної програми для розв’язання пружної задачі.

Оm=7200*2*рі/60;

ro=8.2-5;

Е=1.6е5;

mи=0.3;

Nrb=800;

Hb=20;

Srb=Nrb/Hb;

b=(100)/1000;

a=(30)/1000;

С1=b*b/(b*b-а*а);

n=0;

Stupr=0; STlupr=0; ST2upr=0;

VSTupr=[0]; VSTlupr=[0]; VST2upr=[0];

%3находження вектора кільцевих напружень%

dr-0.005;

Vr=[a:dr:b];

for r=a:dr:b,

n=n+l;

C2upr=l+a^2/r^2;

C3upr=b^2+a^2-(a^2*b^2)/r^2-((l+3*mu)/(3+mu))*r^2;

C4upr=((3+mu)/8)*ro*Om*Om*C3upr;

ST 1 upr=Srb*C 1 *С2ирг+С4uрг;

ST2upr=E*(tetaint(b,alph(r, 1 ),a)*C 1 *C2upr+tetaint(r,alph(r, 1 ),a)-alph(r,l)*temp(r,l));

STupr=ST 1 upr+ST2upr;

VSTupr(n)=STupr;

VST1upr(n)=STlupr;

VST2upr(n)=ST2upr;

end

Vr=[a:dr:b];

n=0

SRupr=0; SRlupr=0; SR2upr=0;

VSRupr=[0]; VSRlupr=[0]; VSR2upr=[0];

I=[ ]

%Знаходження вектора радіальних напружень%

for r=a:dr:b,

n=n+l;

i(n)=n;

C2upr=l-a^2/r^2;

C3upr=b^2+a^2-(a^2*b^2)/r^2-r^2;

Cupr4=((3+mu)/8)*ro*Om*Om*C3upr;

SRlupr=Srb*Cl*C2upr+C4upr;

SR2upr=E*(tetaint(b,(alph(r,l)),a)*Cl*C2upr-tetaint(r,(alph(r,l)),a));

SRupi=SR 1 upr+SR2upr;

VSRupr(n)=SRupr;

VSRlupr(n)=SRlupr;

VSR2upr(n)=SR2upr;

end

%3находження вектора інтенсивності напружень%

VSIupr=sqrt(VSRupr.^2-VSRupr.*VSTupr+VSTupr.^2);

Підпрограми та функції

%Температура%

function t=temp(r,i)

і = 1.4e+004*r(i).^2 - 8.1e+002*r(i) + 9.3е+002;

%Коефіцієнт температурного розширення%

function al=alph(x,i)

al=0;

al=2.02e-014*temp(x,i).^3-5.08e-011*temp(x,i).^2+4.53e-008*temp(x,i)+1.87e-006;

function t=tetaint(x,L,a)

t=(L/x^2)*simp(a,x,500);

%обчислення інтеграла за методом Сімпсона%

function integral=simp(a,b,n)

сlс;

format long;

i=l;

x=[];

Y=[];

x(i)=a;

h=(b-a)/n;

w=0;

Y(i)=0;

while і <n+l,

i=i+l;

x(i)=x(i-l)+h;

if(i/2-floor(i/2))==0

k=4;

else k=2;

end

Y(i)=(h/3)*(x(i)*^;temp(x,i))*k;

end

integral=sum(Y)-(h/3)*(x(i)*temp(x,i));

Додаток 5

Текст комп’ютерної програми для розв’язання задачі з урахуванням повзучості.

СlС;

Оm=7200*2*рі/60;

го=8.2е-5;

t=8760;

еп=3;

Nrb=1800;

Hb=20;

Srb=Nrb/Hb;

b=(100)/1000;

a=(30)/1000;

Cl⁼b*b/(b*b-a*a);

dr=0.005;

Vr=[a:dr:b];

ST=[0], ST1=[0]; ST2=[0];

VST=[0]; VST1=[0]; VST2=[0];

SR=[0]; SR1=[0]; SR2=[0];

VSR=[0]; VSRl=[0]; VSR2=[0];

Szvezd=[];

eps=le-l;

n=0;

for r=a:dnb;

n=n+l;

i(n)=n;

K=l;

Enew(2,n)=1.6e5;

munew(2,n)=0.3;

Enew(l,n)=2e5;

munew(l,n)=0;

while Enew((K),n)-Enew(K+l,n) > eps;

K=K+1;

%SigmaR%

i(n)=n;

C2=1-a^2/r^2;

C3=b^2+a^2-(a^2*b^2)/r^2-r^2;

C4=((3+munew(K,n))/8)*ro*Om*Om*C3;

SRl(n)=Srb*Cl*C2+C4;

SR2(n)=Enew(K,n)*(tetaint(b,(alph(r, 1 )),a)*C 1 *C2-tetaint(r,(alph(r, 1 )),a));

SR(n)=SRl(n)+SR2(n);

SR(n)=SRl(n)+SR2(n);

VSR(n)=SR(n);

%SigmaTeta%

C2=l+a^2/r^2;

CЗ=b^2+a^2-(a^2*b^2)/r^2-((l+3*munew(K,n))/(3+munew(K,n)))*r^2;

C4=((3+munew(K,n))/8)*ro*Om*Om*CЗ;

STl(n)=Srb*Cl*C2+C4;

ST2(n)=Enew(K,n)*(tetaint(b,alph(r,1),a)*C1*C2+tetaint(r,alph(r,1),a)-alph(r,l)*temp(r,l));

ST(n)=STl(n)+ST2(n);

VST(n)=ST(n);

%Sigma i%

VSI(n)=sqrt((VSR(n))^2-VSR(n)*VST(n)+(VST(n))^2);

%Epsilon і elastic&creep%

Epsi(n)=VSI(n)/Enew(K,n);

Epscreep(n)=omegaotte(t).*(VSI(n)^en);

Epssum(n)=Epsi(n)+Epscreep(n);

Szvezd(K,n)=diagram(Epssum,n);

Enew((K+l),n) = Szvezd(K,n)/Epssum(n);

munew((K+1 ),n) = 1/2*( 1 -(1 -2*munew(K,n))*(Enew((K+1 ),n)/Enew(K,n)));

end

end