
Міністерство освіти і науки України
Національний технічний університет України
«Київський політехнічний інститут»
МЕТОДИЧНІ ВКАЗІВКИ
до курсової роботи з дисципліни
«Теорія пластичності і повзучості»

Міністерство освіти і науки України
Національний технічний університет України
«Київський політехнічний інститут»
МЕТОДИЧНІ ВКАЗІВКИ
до курсової роботи з дисципліни
«Теорія пластичності і повзучості»
для студентів механічних спеціальностей
Затверджено Методичною радою НТУУ «КПІ»
Київ
«Політехніка»
2003
Методичні вказівки до курсової роботи з дисципліни «Теорія пластичності і повзучості» для студ. мех. спец. / Уклад.: М. І. Бобир, В. М. Можаровський. – К.: ІВЦ “Видавництво «Політехніка»”, 2003. – 28 с.
Гриф надано Методичною радою НТУУ «КПІ»
(Протокол № 6 від 20.03.2003 р.)
Укладачі: М. І. Бобир
В. М. Можаровський
Відповідальний редактор М. І. Бобир, д-р техн. наук, проф.
Рецензент С. М. Шукаєв, д-р техн. наук, проф.
ВСТУП
Мета курсової роботи з курсу «Теорія пластичності і повзучості» – закріпити та поглибити набуті знання у результаті вивчення цього курсу, опанувати основні методи розрахунків напружено-деформованого стану елементів конструкцій в умовах пружно-пластичного деформування та з урахуванням реологічних властивостей конструктивних матеріалів. При цьому передбачаються також знання попередніх теоретичних курсів з математики, фізики, опору матеріалів, теорії пружності.
Для досягнення поставленої мети студенту пропонується на вибір виконати розрахунок напружено-деформованого стану конкретного елемента конструкції, який працює в умовах складного термосилового навантаження за заданих граничних умов. Основну тематику курсового проектування наведено в дод. 1.
Для студентів, які активно беруть участь у науково-дослідних роботах кафедри динаміки, міцності машин та опору матеріалів, інших кафедр НТУУ «КПІ», а також філіалів кафедри, тематика їх курсової роботи може бути пов’язана з цими дослідженнями.
Курсова робота може бути складовою частиною дипломного проекту, який включає розрахунок такого самого конструктивного елемента, але в ширшому спектрі (наприклад, не тільки розрахунок у пружно-пластичній області, а і з урахуванням коливальних процесів, вібраційних навантажень, стійкості, витривалості та ін.).
Розв’язувати ту чи іншу задачу курсової роботи потрібно за сучасними теоретичними і практичними методами. З цією метою належить глибоко проаналізувати рекомендовані літературні джерела, виконати критичний огляд стану наукової та інженерної проблеми і вибрати кращий сучасний метод розв’язання поставленої задачі.
У процесі курсового проектування з теорії пластичності та повзучості студенти набувають досвіду і практичних навиків розв’язання складніших актуальних інженерних завдань.
Таким чином, основним завданням курсового проектування є розвиток творчих навиків, інженерної ініціативи та наукового пошуку з розв’язання поставлених завдань сучасними методами.
Загальні вимоги до виконання та оформлення курсової роботи
1. Провести критичний аналіз рекомендованої літератури та скласти огляд основних літературних джерел із заданої теми курсової роботи.
2. Обґрунтувати постановку завдання.
3. Детально викласти вибраний метод розв’язання задачі.
4. Навести основні конкретні результати розв’язання задачі з відповідним програмним забезпеченням.
5. У курсовій роботі відобразити особистий вклад студента у розв’язання наукового та інженерного завдання.
6. Результати розв’язання задачі довести до числа з побудовою відповідних графіків та епюр (з використанням ПЕОМ).
7. Текстову частину курсової роботи потрібно надрукувати, а графічну частину обсягом 4 – 5 листів формату А2 оформити з використанням програм МАТСАD, МАТLАВ та (або) AutoCAD.
Загальні вказівки
Тему курсової роботи видають студентам на бланку встановленого зразка (Завдання до курсової роботи з «Теорії пластичності та повзучості»), в якому наведено основну рекомендовану літературу. Студенту потрібно детально проаналізувати сучасний стан розв’язання цього типу задач за додатковими літературними джерелами. Бланк завдання за підписом керівника є обов’язковою частиною пояснювальної записки до курсової роботи.
Пояснювальну записку до курсової роботи виконують у вигляді журналу форматом А4 з титульним аркушем (дод. 2). Текст записки виконують у рукописному або друкованому варіанті на папері названого розміру.
Текст записки поділяють на параграфи відповідно до пунктів завдання. Формули пояснювальної записки повинні мати наскрізну нумерацію.
Графічну частину пояснювальної записки виконують на папері формату А2 з кутовим штампом (дод. 3).
На плакатах наводять схему розраховуваного об’єкта, основні рівняння, метод їх розв’язання та основні отримані результати (таблиці, графіки тощо).
Як приклад розглянемо тему курсової роботи «Деформування дисків газотурбінних двигунів в умовах сталої повзучості з урахуванням температурних напружень».
Розраховуючи напружено-деформований стан дисків газотурбінних двигунів в умовах термосилового експлуатаційного навантаження, потрібно враховувати деформації повзучості. Для дисків на стадії їх інженерного проектування визначення кінетики накопичення деформацій неізотермічної повзучості, що супроводжує цей процес, є важливим інженерним завданням.
Постановка задачі: визначити напружено-деформований стан диска газотурбінного двигуна на стадії сталої повзучості з урахуванням температури.
Метод. На сьогодні є декілька різних методів розрахунку напружено-деформованого стану дисків в умовах повзучості. Основні методи такого розрахунку наведено в працях М. М. Малініна [7], Л. М. Качанова [6], М. С. Можаровського [9], Ю. М. Работнова [14] та І. А. Бергера [3].
Для розв’язання поставленої задачі використаємо метод розрахунку дисків та сталу повзучості, що запропонував М. М. Малінін [7] та І. А. Бергер [3].
Основні рівняння для розрахунку напружено-деформованого стану дисків газотурбінних двигунів на сталу повзучість. Розглянемо симетричний відносно своєї серединної поверхні диск. Робимо припущення, що його товщина h є малою порівняно із зовнішнім радіусом r = b.
Припустимо, що відцентрові сили, які виникають за рахунок обертання диска з кутовою швидкістю , рівномірно розподілені по товщині диска h.
Диск нерівномірно нагрітий по радіусу r. Температуру вважаємо постійною по товщині диску.
Напружений стан диска вважаємо двовимірним і осесиметричним (z = 0); поздовжнє z та кільцеві напруження рівномірно розподілені по товщині диску (рис. 1).
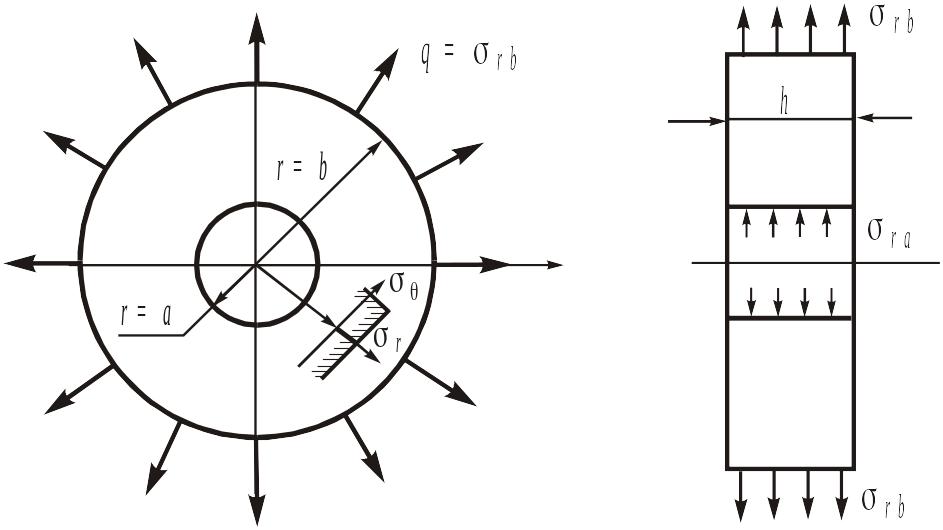
Рис. 1. Розрахункова схема обертового диска
Такі припущення спрощують розрахунок, але разом з тим вносять деякі похибки в точності розрахунку напружено-деформованого стану. Ці похибки тим менші, чим менша порівняно з діаметром диска його товщина та чим плавніше вона змінюється залежно від радіуса.
Розглянемо нескінченно малий елемент диска (рис. 2).
На цей елемент, крім кільцевих та радіальних r напружень, діють об’ємні сили qr.
Умова рівноваги цього елемента має вигляд
![]()
або
![]() (1)
(1)
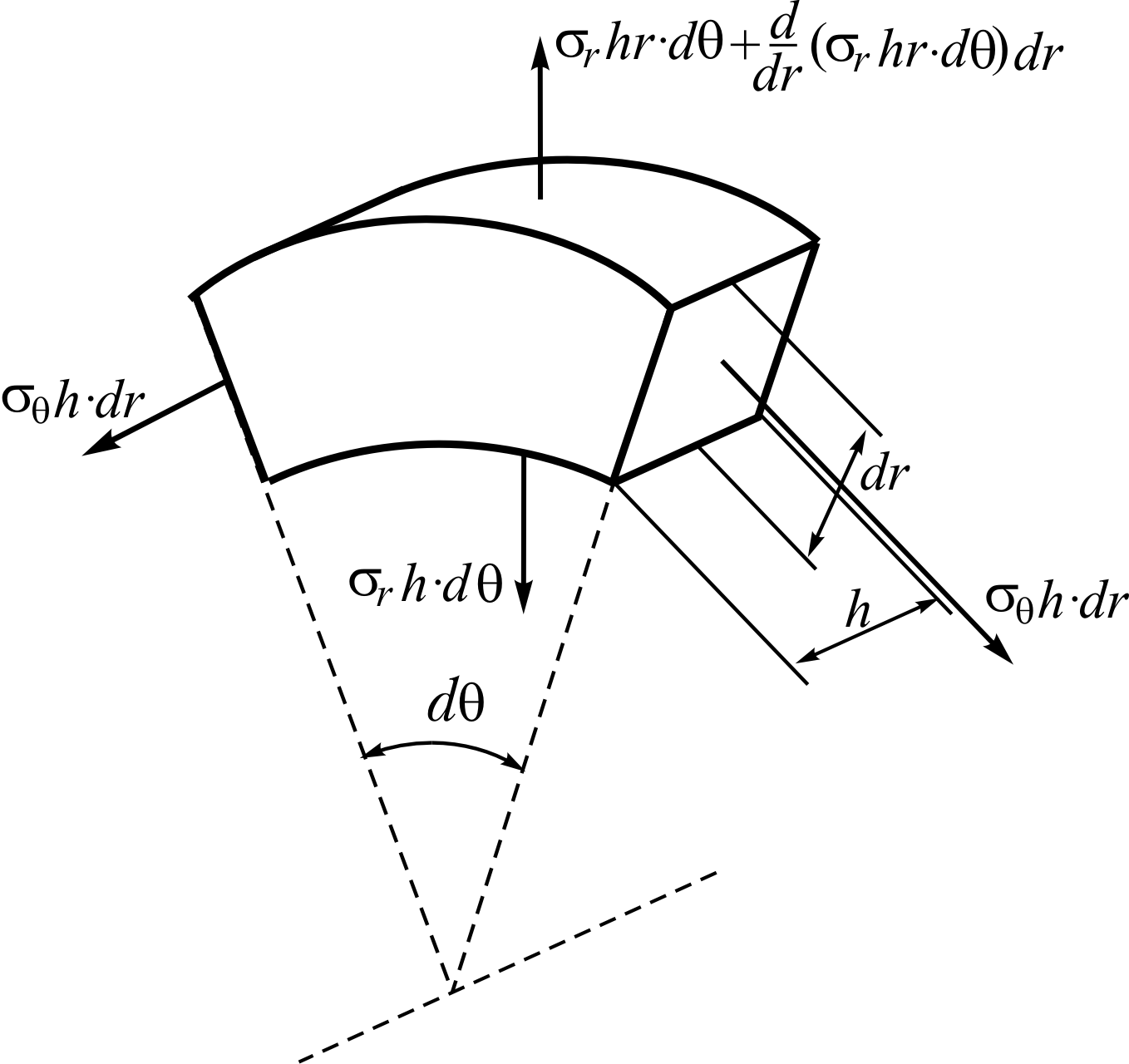
Рис. 2. Розрахунковий елемент обертового диска
Об’ємне навантаження, зумовлене дією відцентрових сил,
![]()
де – густина матеріалу, з якого виготовлено диск.
Геометрична частина задачі. Позначимо переміщення точок диска в радіальному напрямі через u(r). Тоді деформації в радіальному r та кільцевому напрямі матимуть вигляд
![]()
![]() (2)
(2)
Ураховуємо,
що в початковий момент часу (t = 0)
виникають тільки пружні деформації
(![]() ).
За експлуатаційних режимів до них
добавляються деформації
повзучості з компонентами
).
За експлуатаційних режимів до них
добавляються деформації
повзучості з компонентами
![]() .
Тоді загальна деформація складається
з таких складових:
.
Тоді загальна деформація складається
з таких складових:
![]()
У межах пружності зв’язок між деформаціями та напруженнями виражається законом Гука:
![]() (3)
(3)
де
![]() – модуль пружності матеріалу диска;
– модуль пружності матеріалу диска;
![]() – коефіцієнт Пуассона; Т –
температура диска;
– коефіцієнт Пуассона; Т –
температура диска;
![]() – коефіцієнт лінійного розширення
матеріалу.
– коефіцієнт лінійного розширення
матеріалу.
Якщо підставити (3) в залежність (2), то одержимо
 (4)
(4)
Рівняння сумісності деформацій для диска має вигляд
![]() (5)
(5)
З урахуванням (3) із залежності (5) маємо
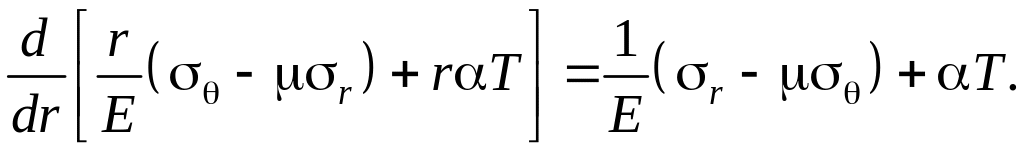
Підставляємо рівняння (4) в (1). У результаті отримуємо диференціальне рівняння для тиску в переміщеннях:
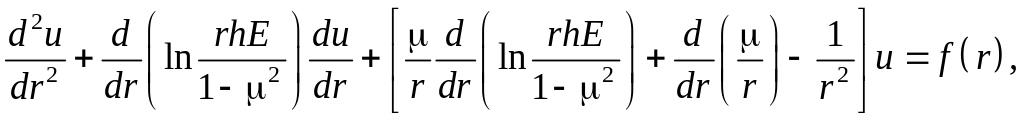 (6)
(6)
де
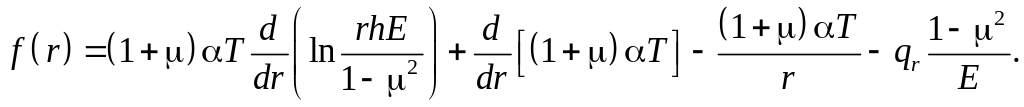
У
свою чергу,
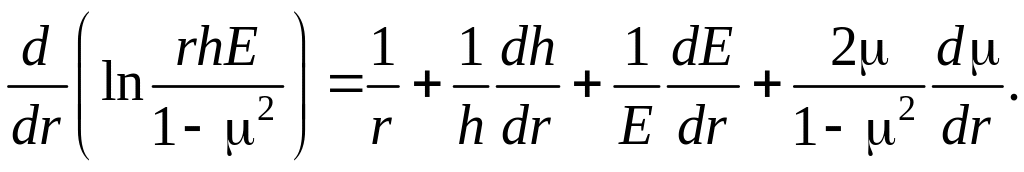
У загальному випадку залежність (6) – це лінійне диференціальне рівняння другого порядку зі змінними коефіцієнтами. З урахуванням граничних умов для функцій u(r) на контурах r = a та r = b його розраховують одним із числових методів.
Позначимо лінійно незалежні розв’язки однорідного рівняння типу (6) через u1(r) та u2(r). Тоді загальний розв’язок неоднорідного рівняння (6) матиме вигляд
![]()
де K1
та K2
– довільні постійні;
![]() – частковий розв’язок,
який буде знайдено за допомогою методу
варіацій довільних постійних. Згідно
із цим методом частковий розв’язок
рівняння (6) має вигляд
– частковий розв’язок,
який буде знайдено за допомогою методу
варіацій довільних постійних. Згідно
із цим методом частковий розв’язок
рівняння (6) має вигляд
![]() (7)
(7)
При цьому
![]() (8)
(8)
Якщо
два рази продиференціювати (7) за умови
(8) і підставити в рівняння (6), то одержимо
систему рівнянь для визначення
![]() і
і
![]() :
:
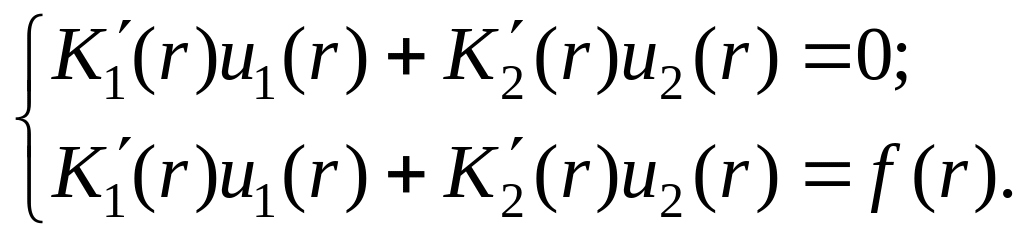 (9)
(9)
Зважаючи
на лінійну незалежність розв’язків
![]() і
і
![]() ,
визначник цієї системи можна записати
так:
,
визначник цієї системи можна записати
так:
![]() (10)
(10)
Систему
(9) можна розв’язати відносно
![]() і
і
![]() .
Інтегруючи (10), знаходимо
і
.
Якщо підставити їх значення в рівняння
(7), то рівняння (6) набуде у вигляду
.
Інтегруючи (10), знаходимо
і
.
Якщо підставити їх значення в рівняння
(7), то рівняння (6) набуде у вигляду
![]() (11)
(11)
де
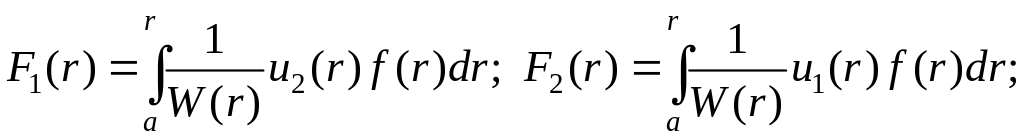
![]() і
і
![]() – постійні інтегрування.
– постійні інтегрування.
Якщо продиференціювати (11) з урахуванням (9) та підставити у вирази для r і (4), то в загальному вигляді напруження в диску
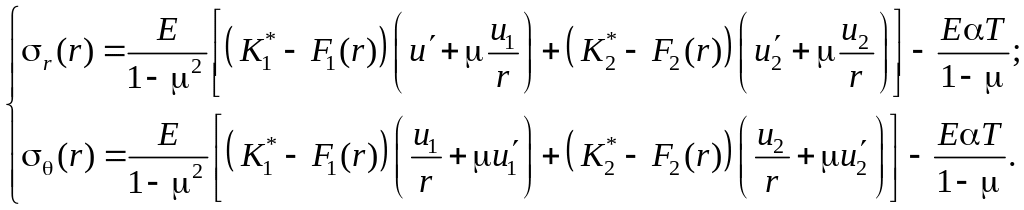
Довільні
постійні
і
![]() можна виразити через радіальні напруження
rа
та rb
в диску.
можна виразити через радіальні напруження
rа
та rb
в диску.
Уведемо позначення:
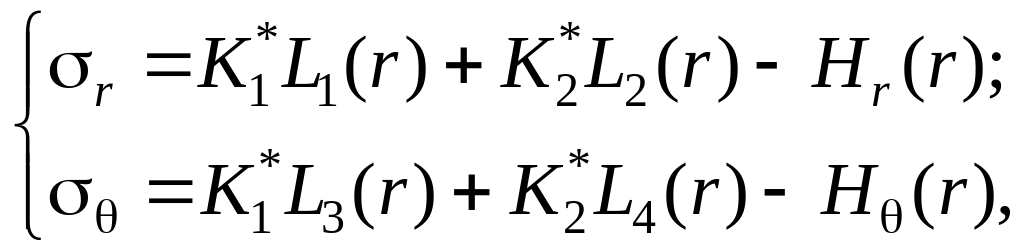 (12)
(12)
де
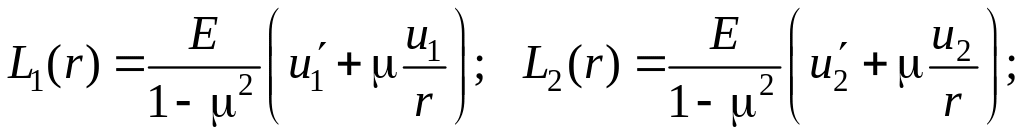
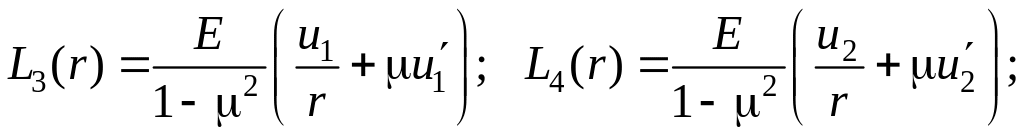
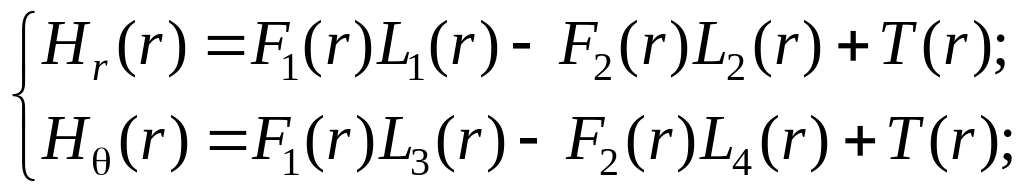

Підставимо в рівняння (12) граничні умови для диска з центральним отвором:
![]()
Тоді:
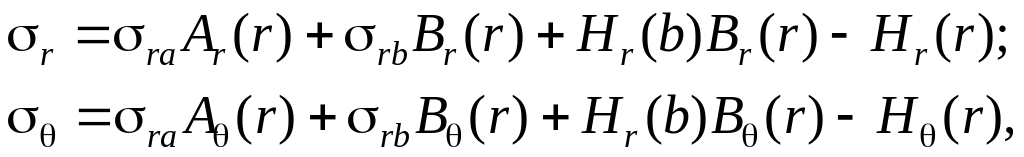
де
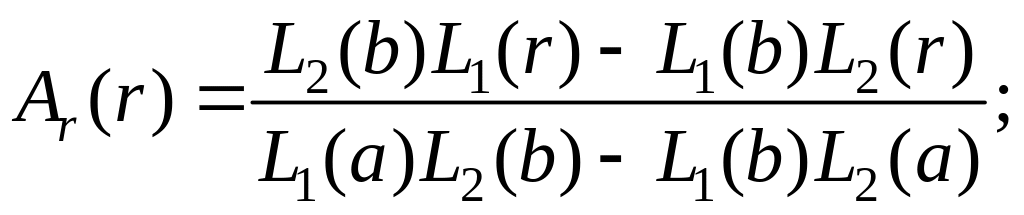



Для диска з постійною товщиною та постійними параметрами пружності диференціальне рівняння (6) набуде вигляду
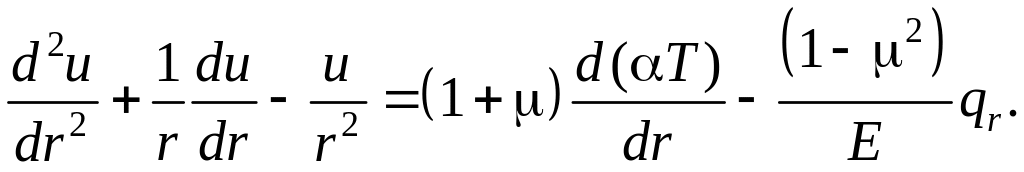
Розв’язком
відповідного однорідного рівняння є:
![]() .
Визначник (10) системи (9) набуде вигляду:
.
Визначник (10) системи (9) набуде вигляду:
![]() .
Загальний розв’язок для напружень в
диску постійної товщини такий:
.
Загальний розв’язок для напружень в
диску постійної товщини такий:
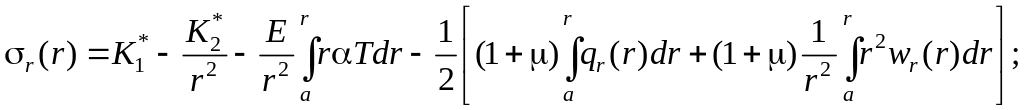 (13)
(13)
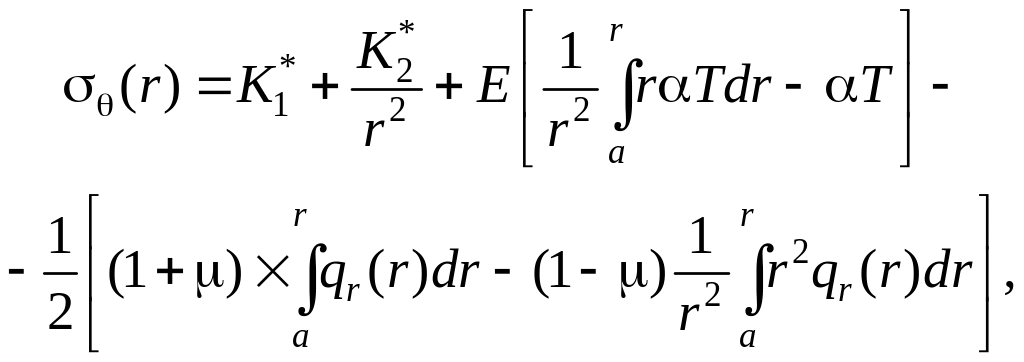 (14)
(14)
де і – постійні, які визначаються із граничних умов.
Для обертового диска з урахуванням відцентрових сил із залежностей (13) та (14) отримаємо:

де
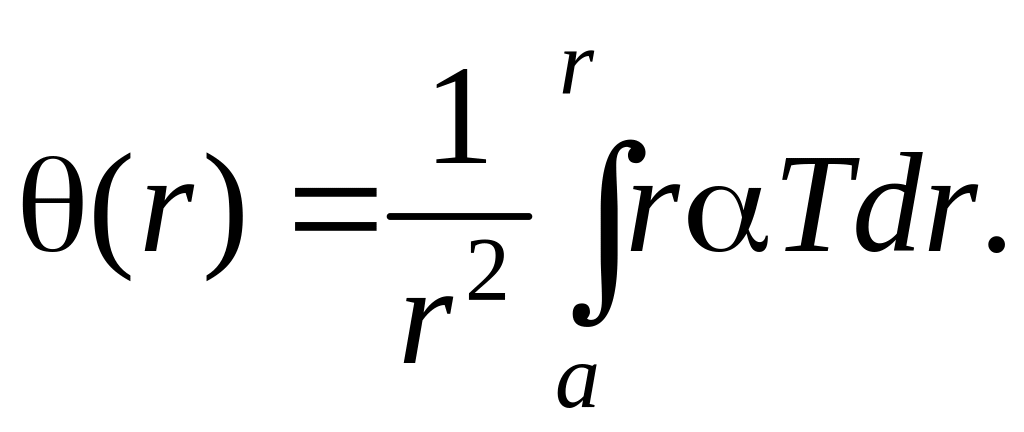
Для диска з центральним отвором напруження визначаємо:
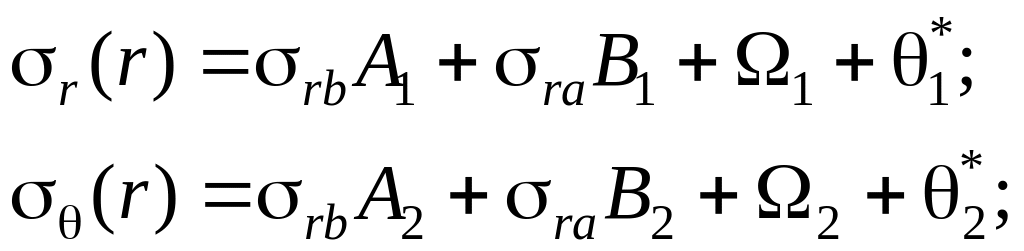 (15)
(15)
де 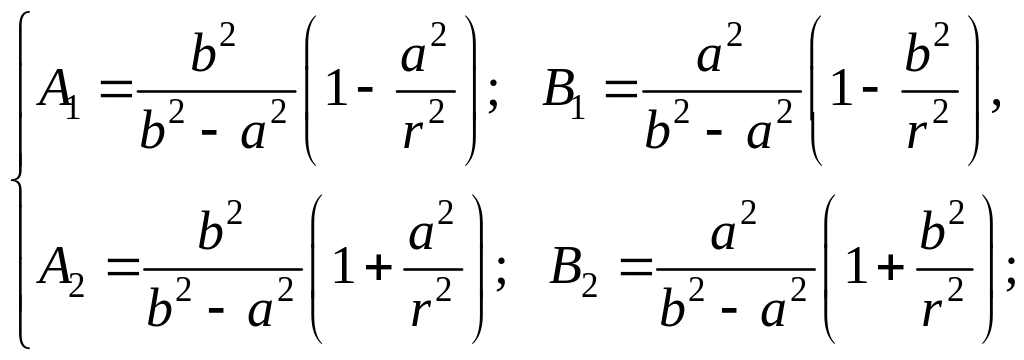 (16)
(16)
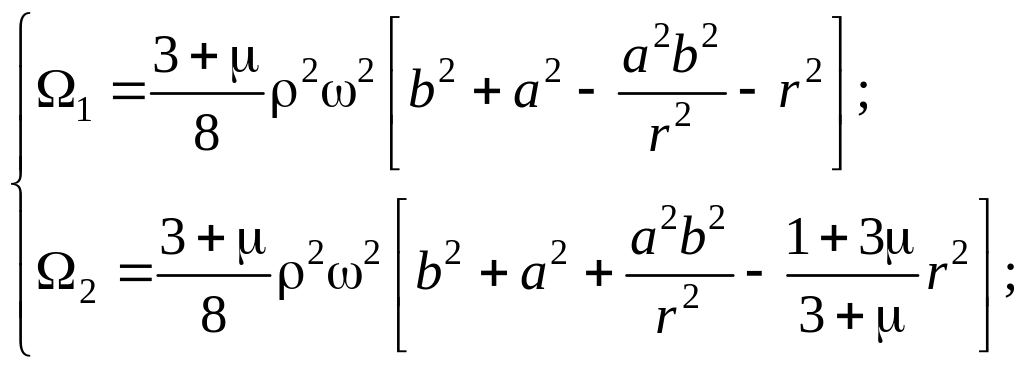 (17)
(17)
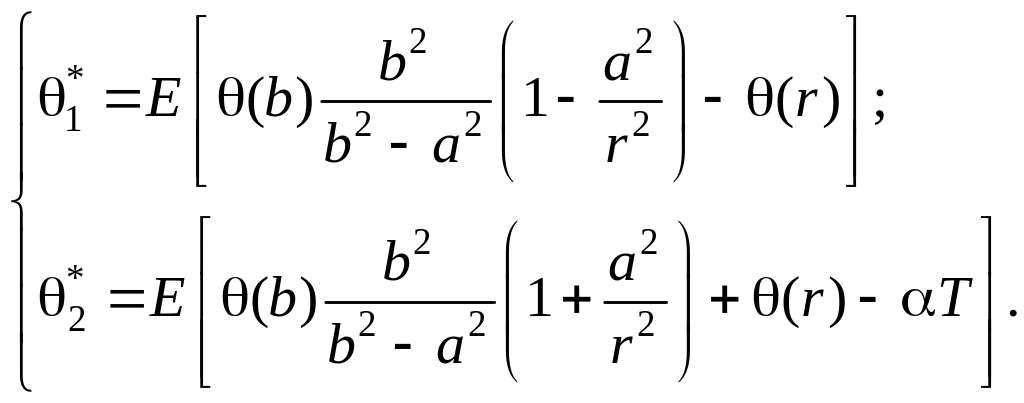 (18)
(18)
Переміщення
в диску з отвором можна знайти з рівняння
(2) з урахуванням (3). Якщо підставити в
них
![]() і
і
![]() із (15), то
із (15), то
![]()
На
зовнішньому контурі при
![]() матимемо:
матимемо:
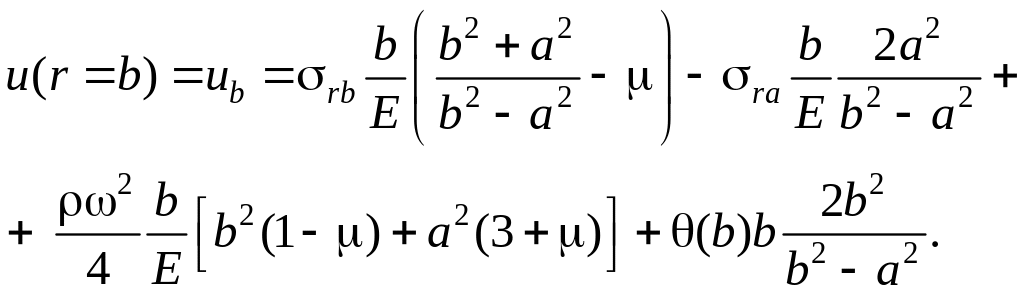
Граничні
умови задаються у вигляді напружень,
що діють на внутрішньому
![]() та зовнішньому
та зовнішньому
![]() радіусах (див. рис. 1).
радіусах (див. рис. 1).
Якщо диск посаджено на вал за допомогою шпонки, то радіальні напруження на внутрішньому радіусі дорівнюють нулю:
![]() (35)
(35)
Граничну умову на зовнішньому радіусі задають таким чином. З експлуатаційних умов відоме радіальне навантаження Nrb, що припадає на одиницю довжини дуги диску. Розділимо Nrb на ширину диску. В результаті одержуємо радіальне напруження при r = b:
![]() (20)
(20)
Якщо підставити граничну умову (19) в залежність (15) і врахувати рівняння (16) – (18), то можна отримати рівняння для напружень у диску, що посаджений на вал за допомогою шпонки:
 (21)
(21)
Для
прикладу розглянемо диск з такими
розмірами: а = 30 мм;
b = 100 мм;
h = 20 мм.
Диск виготовлено з нікелевого сплаву
типу ХН35ВМТ, який широко використовують
для виготовлення робочих лопаток та
дисків газових турбін. Цей сплав має
такі фізико-механічні властивості [17]:
![]() Е = 1,60·105 МПа
(для Т = 650 °С);
= 0,3.
Розподіл температури по радіусу диска
показано на рис. 3. Графік залежності
коефіцієнта лінійного розширення
матеріалу від температури зображено
на рис. 4.
Е = 1,60·105 МПа
(для Т = 650 °С);
= 0,3.
Розподіл температури по радіусу диска
показано на рис. 3. Графік залежності
коефіцієнта лінійного розширення
матеріалу від температури зображено
на рис. 4.
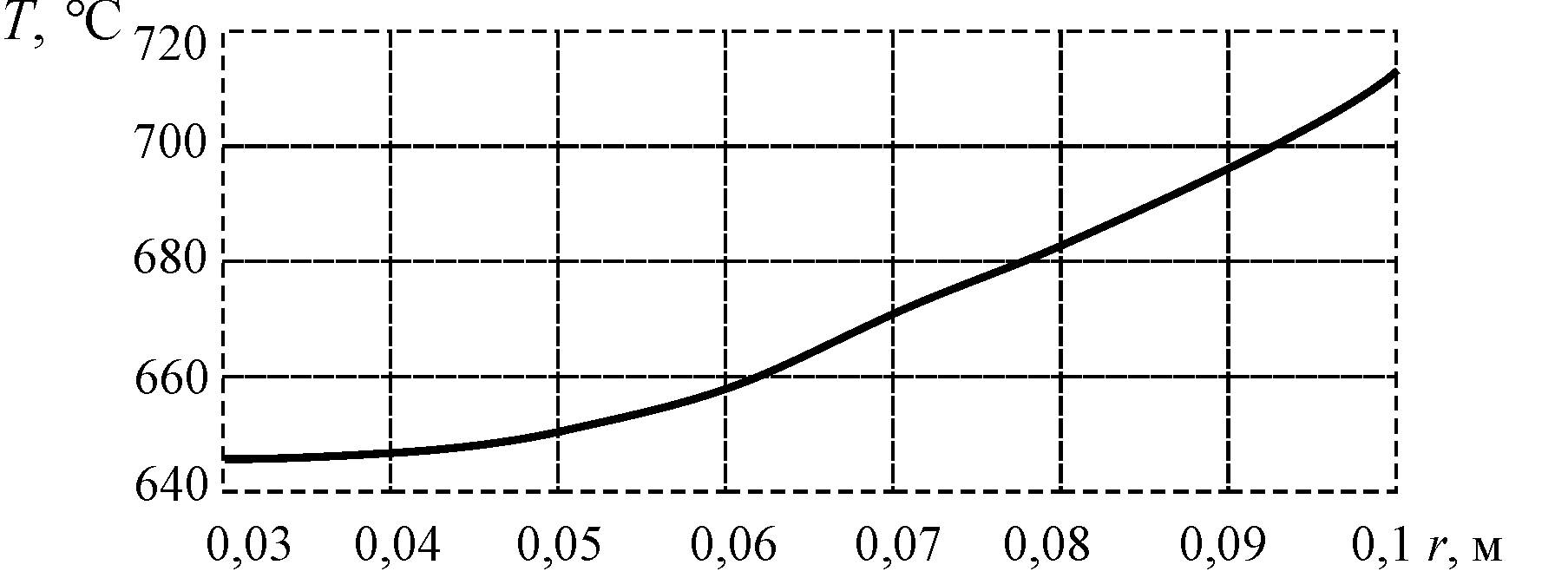
Рис. 3. Розподіл температури залежно від радіуса диска
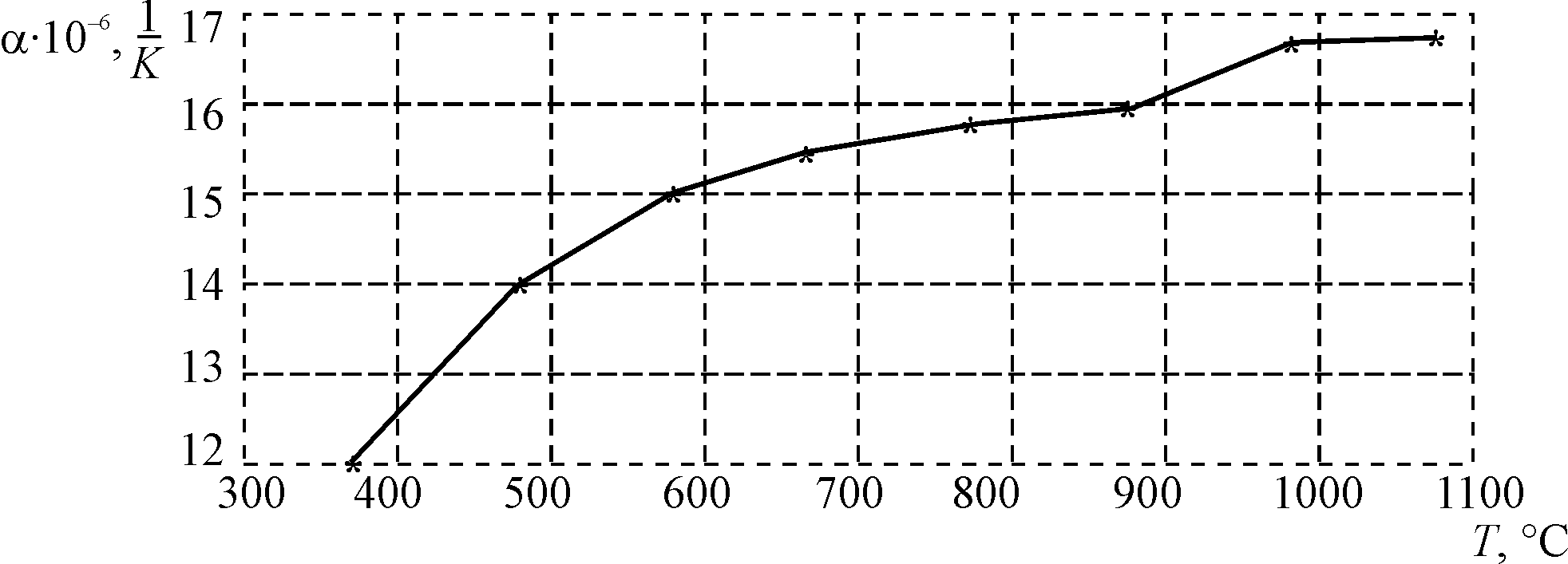
Рис. 4. Залежність коефіцієнта лінійного розширення матеріалу від температури
Згідно
з рекомендаціями [3] радіальне навантаження
Nrb = 800 Н/мм.
Тоді напруження на межі внутрішнього
радіуса (залежність (20)) дорівнює:
rb = 40 МПа.
Кількість обертів диска за хвилину
n* = 7200 об/хв.
Тоді кутова швидкість обертання диска
становитиме:

1. Розрахунок задачі в межах пружності. Розрахунок виконуємо, використовуючи пакет прикладних програм MATLAB 6.5. Програму для обчислень напружень наведено в дод. 4.
Алгоритм обчислення:
1) задаємо початкові параметри;
2) покладемо
![]() ;
;
3) розраховуємо пружну задачу згідно з (15) та (21);
4) надаємо радіусу диска r деякий кінцевий приріст dr;
5) переходимо до п. 1.3;
6) цикл згідно з пп. 1.3 і 1.4 зупиняємо, коли значення радіуса r = b.
У результаті обчислень знаходимо кільцеві та радіальні r напруження у m різних радіусах диска, де m розраховуємо за формулою
![]() (22)
(22)
Результати обчислень для dr = 5 мм наведено в табл. 1.
Таблиця 1. Напруження в диску
r, м |
|
|
|
r, м |
|
|
|
0,030 |
0 |
0 |
0 |
0,030 |
87,919 |
78,056 |
165,9755 |
0,035 |
11,743 |
10,482 |
22,226 |
0,35 |
76,305 |
66,279 |
142,5845 |
0,040 |
19,312 |
17,005 |
36,317 |
0,040 |
68,765 |
56,649 |
125,4139 |
0,045 |
24,502 |
21,042 |
45,544 |
0,045 |
63,594 |
47,688 |
111,2819 |
0,050 |
28,213 |
23,368 |
51,581 |
0,050 |
59,893 |
38,619 |
98,5121 |
0,055 |
30,960 |
24,420 |
55,380 |
0,055 |
57,153 |
28,999 |
86,1516 |
0,060 |
33,049 |
24,461 |
57,510 |
0,060 |
55,067 |
18,558 |
73,6246 |
0,065 |
34,674 |
23,655 |
58,329 |
0,065 |
53,441 |
7,1235 |
60,5648 |
0,070 |
35,964 |
22,108 |
58,072 |
0,070 |
52,150 |
-5,4216 |
46,7280 |
0,075 |
37,005 |
19,892 |
56,897 |
0,075 |
51,106 |
-19,161 |
31,9444 |
0,080 |
37,856 |
17,054 |
54,910 |
0,080 |
50,249 |
-34,159 |
16,0905 |
0,085 |
38,562 |
13,627 |
52,189 |
0,085 |
49,537 |
-50,465 |
-0,9276 |
0,090 |
39,154 |
9,630 |
48,788 |
0,090 |
48,939 |
-68,124 |
-19,1851 |
0,095 |
39,654 |
5,0886 |
44,743 |
0,095 |
48,430 |
-87,175 |
-38,7455 |
0,100 |
40,082 |
0 |
40,082 |
0,100 |
47,994 |
-107,66 |
-59,6653 |
2. Розрахунок
напружено-деформованого стану диска в
умовах сталої повзучості виконуємо
методом змінних параметрів пружності.
Скористаємось основними рівняннями
теорії малих пружно-пластичних деформацій.
Згідно з цією теорією інтенсивність
деформацій
![]() складається з інтенсивності пружних
деформацій
складається з інтенсивності пружних
деформацій
![]() та інтенсивності деформацій повзучості
та інтенсивності деформацій повзучості
![]() :
:
![]() (23)
(23)
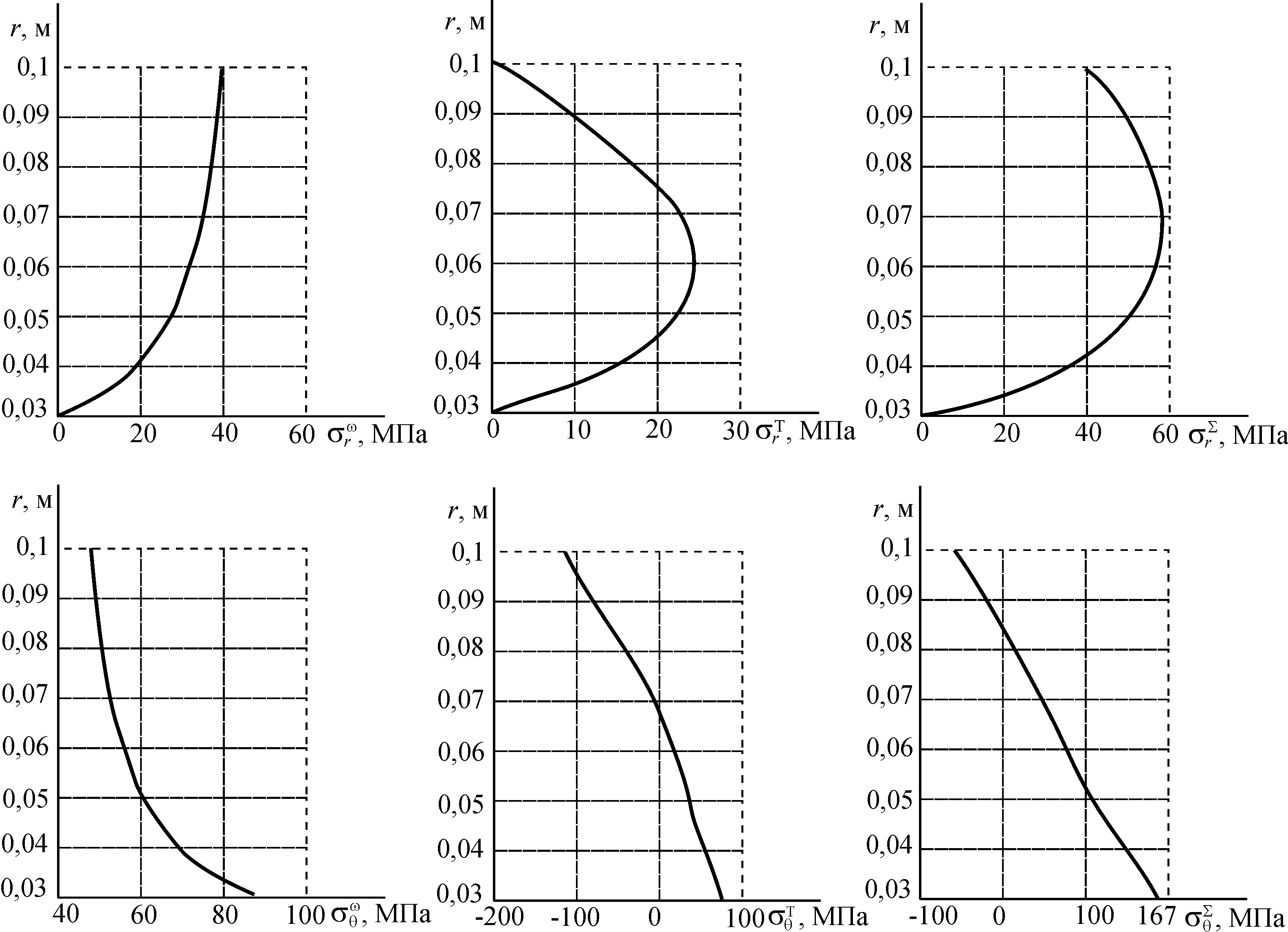
Рис. 5. Залежність складових тензора напружень від радіуса диска в межах пружності
Залежність між інтенсивністю деформацій повзучості та інтенсивністю напружень на сталому участку кривої повзучості вважаймо степеневою:
![]() (42)
(42)
де
![]() – функція часу; n –
показник.
– функція часу; n –
показник.
Для
нікелевих сплавів
![]() [17]. Функцію
[17]. Функцію
![]() для сплаву ХН35ВМТ показано на рис. 6.
для сплаву ХН35ВМТ показано на рис. 6.
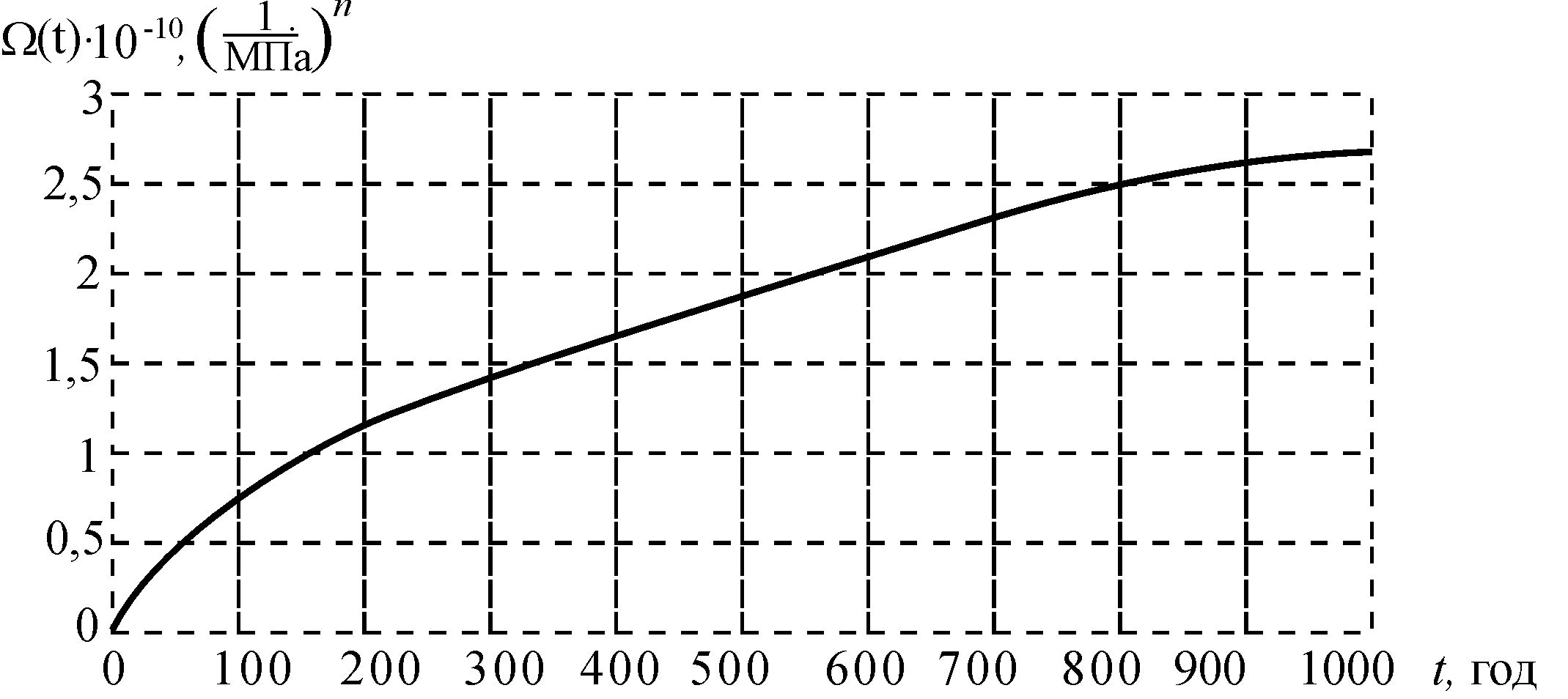
Рис. 6. Залежність функцій повзучості для сплаву ХН35ВМТ від часу
Залежність (23) з урахуванням (24) набуде вигляду
![]()
У
розрахунках час
![]() дорівнює 8760 год, що відповідає одному
року експлуатації диска.
дорівнює 8760 год, що відповідає одному
року експлуатації диска.
Розрахунок
виконуємо методом змінних параметрів
пружності. Для процесів сталої повзучості
використаємо теорію старіння. Перебудуємо
криві повзучості с = f (t)
в ізохронні криві = f ()
при декількох температурах досліджень
(рис. 7). Для розрахунку на повзучість
нерівномірно нагрітого диска теорію
старіння можна наближено використовувати
в тих випадках, коли температурні
напруження або взагалі не виникають,
або суттєво менші від напружень зовнішніх
сил. Розрахунки для довільно фіксованого
моменту часу
виконують за формулами деформаційної
теорії термопластичності, але замість
кривих деформування використовують
сім’ю ізохронних кривих
![]() .
Такі ізотропні криві показано на рис.
7. При цьому крива t = 0
відповідає для одноосьового напруженого
стану діаграмі розтягу. Якщо взяти
окрему ізохронну криву (рис. 8) для
конкретного часу
,
то можна згідно з методом змінних
параметрів пружності одержати
закономірність розподілу напружень і
деформацій для конкретного часу
експлуатації конструктивного елемента
(наприклад,
.
Такі ізотропні криві показано на рис.
7. При цьому крива t = 0
відповідає для одноосьового напруженого
стану діаграмі розтягу. Якщо взяти
окрему ізохронну криву (рис. 8) для
конкретного часу
,
то можна згідно з методом змінних
параметрів пружності одержати
закономірність розподілу напружень і
деформацій для конкретного часу
експлуатації конструктивного елемента
(наприклад,
![]() (рис. 8)). Змінні параметри пружності
визначають згідно з рівняннями:
(рис. 8)). Змінні параметри пружності
визначають згідно з рівняннями:
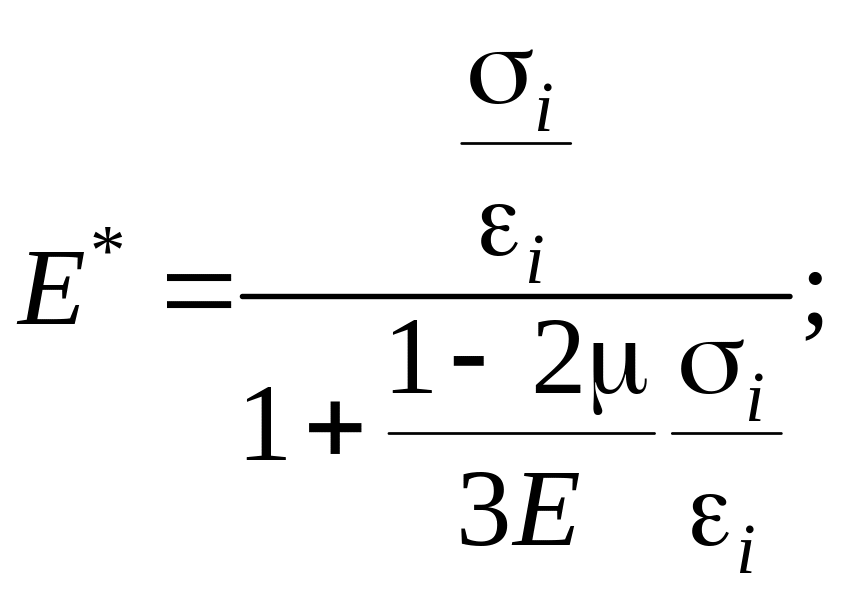

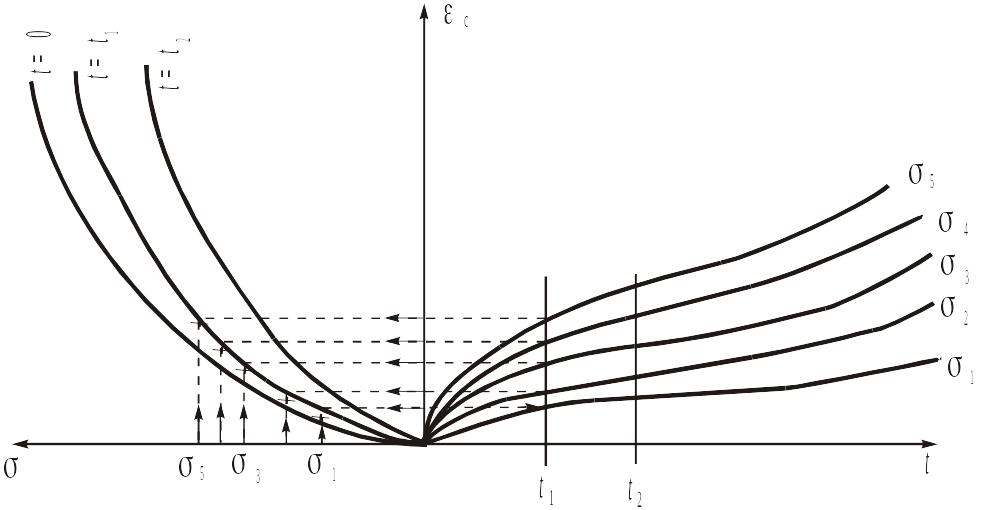
Рис. 7. Методика побудови ізохронних кривих повзучості
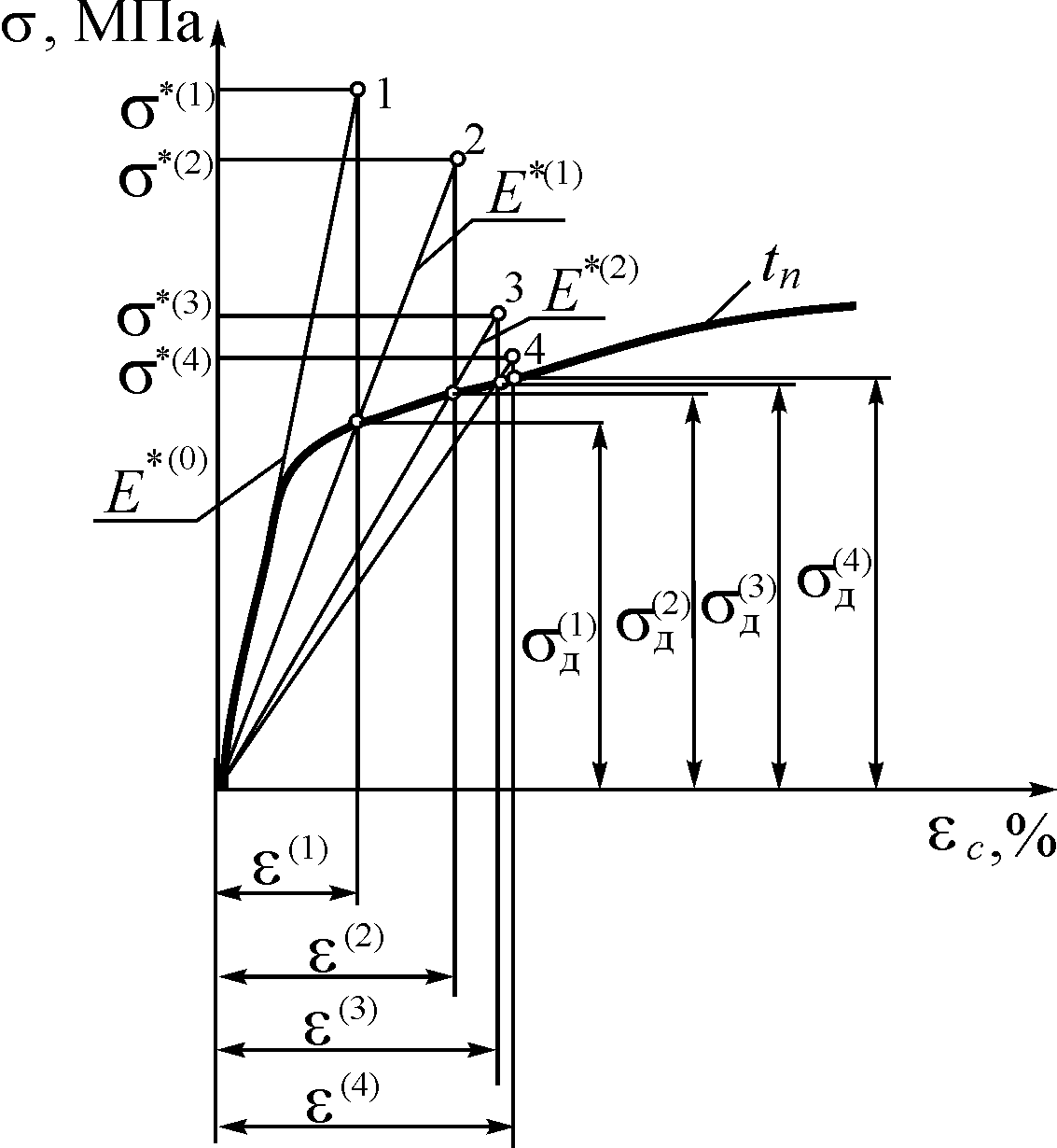
Рис. 8. Ізохронна крива повзучості та схема використання методу змінних параметрів пружності
Розрахунок виконуємо за допомогою послідовних наближень.
У першому наближенні беремо
![]()
![]()
де
![]() та
та
![]() згідно з рис. 8 визначаємо за аналогією
з модулем пружності та коефіцієнтом
Пуассона у разі розрахунків у пружній
області.
згідно з рис. 8 визначаємо за аналогією
з модулем пружності та коефіцієнтом
Пуассона у разі розрахунків у пружній
області.
Розв’язуючи пружну задачу, знаходимо за формулою (23) інтенсивність напружень у кожній з m розрахункових точок (залежність (22)). У результаті знаходимо точку 1 (рис. 8), якій відповідає деформація
![]()
За ізохронною кривою для цього значення деформації дістаємо відповідне їй напруження:
![]()
Потім
знаходимо новий січний модуль
![]() :
:
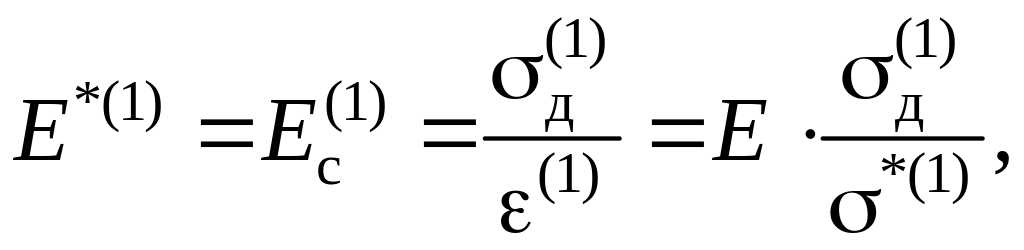
де
![]() – січний модуль ізохронної діаграми
для відповідної ітерації.
– січний модуль ізохронної діаграми
для відповідної ітерації.
Новий коефіцієнт Пуассона визначаємо таким чином:
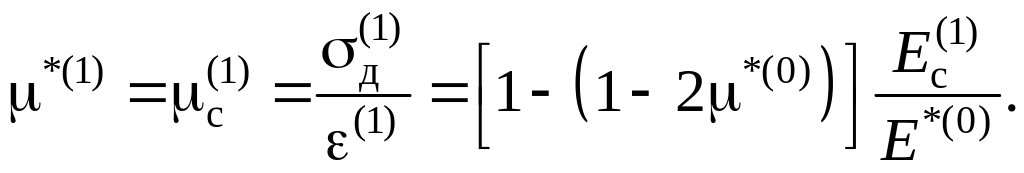
Розв’яжемо
ще раз таку саму пружну задачу з
параметрами
![]() .
.
У результаті отримаємо новий стан 2 (див. рис. 8). Причому:
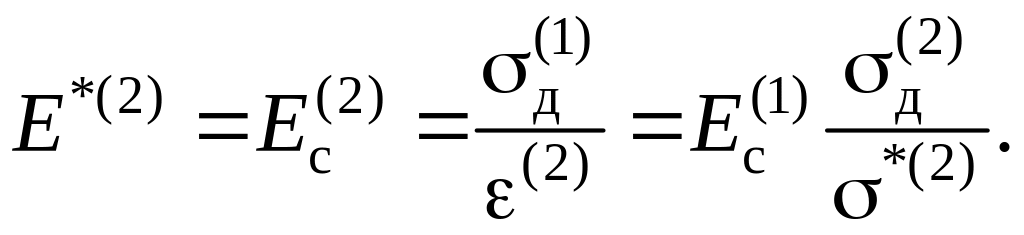
За
заданих навантажень і температур
продовжуємо розрахунок доти, доки
відношення січних модулів
![]() та
та
![]() на j-й
інерції не стане меншим за деяку малу
наперед задану величину.
на j-й
інерції не стане меншим за деяку малу
наперед задану величину.
Програму розрахунків показано в дод. 4 та 5.
Результати
розрахунків для заданої ізохронної
кривої за компонентами
![]() та
та
![]() ,
а також інтенсивності напружень
,
а також інтенсивності напружень
![]() ілюструє рис. 9, де пунктирні лінії –
пружний розрахунок, а суцільні –
розрахунок з урахуванням повзучості.
ілюструє рис. 9, де пунктирні лінії –
пружний розрахунок, а суцільні –
розрахунок з урахуванням повзучості.
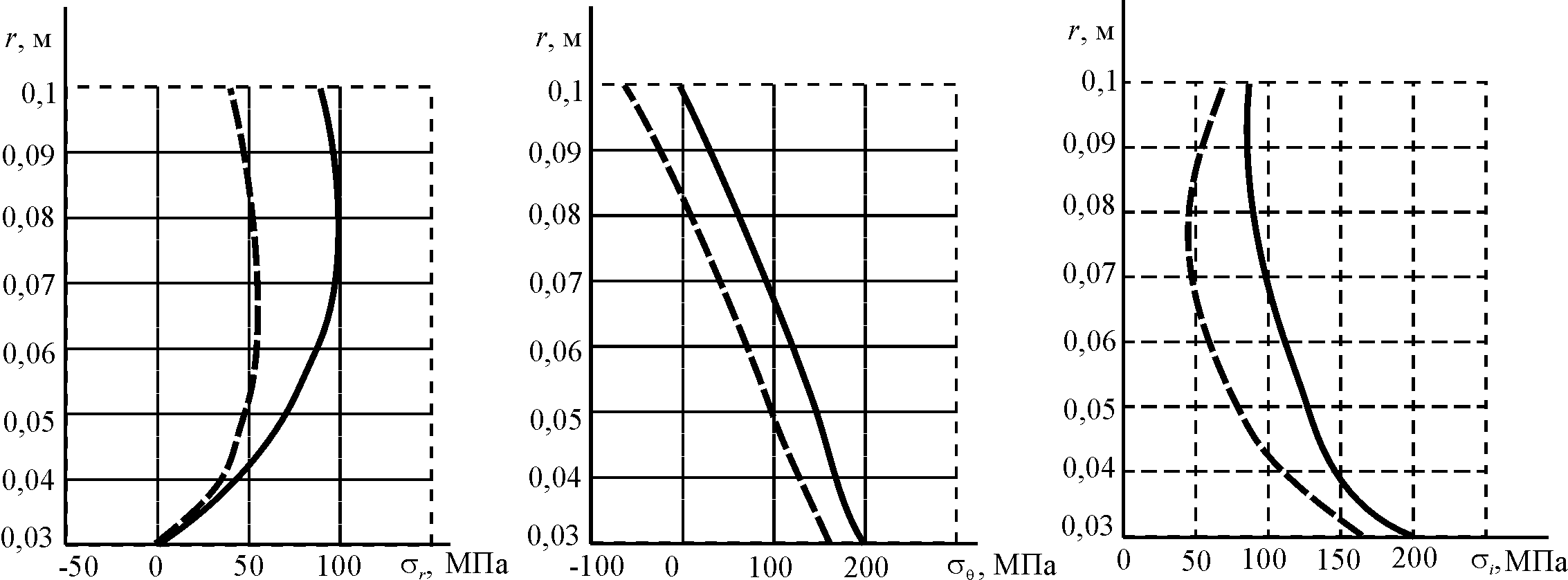
Рис. 9. Розподіл напружень залежно від радіуса диска в межах пружності та з урахуванням повзучості
Таким чином, у результаті річної експлуатації диска за заданих термосилових параметрів отримаємо збільшення напружень.
