Билет №1

1) Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси: суммарный момент сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение:  . Учитывая, что момент импульса твердого тела  , уравнение динамики твердого тела можно представить в виде: .

Момент инерции тела   относительно любой оси вращения (Теорема Штейнера) равен моменту инерции   относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы   тела на квадрат расстояния    между осями:  .

2 )  Тангенциальное ускорение – составляющая ускорения мат. Точки, направленная по касательной к траектории и характеризующая быстроту изменения величины скорости. [м/с^2]

Билет №2

1) Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте.

Монохроматическая волна — строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой. Делится на бегущую и стоячую.

СФЕРИЧЕСКАЯ ВОЛНА - волна, радиально расходящаяся от некоторой точки (источника) или сходящаяся к ней (к стоку) и имеющая сферич. волновые фронты (поверхности равных фаз). Простейшим примером является сферически симметричная скалярная волна вида:

2) Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению. Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:  [м/с^2]

Б илет №3

1) Сложение гармонических колебания одного направления:

 Taк как векторы A₁ и A₂ вращаются с одинаковой угловой скоростью ω₀, то разность фаз (φ₂ - φ₁) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет    (1) В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями:  

 

Сложение двух гармонических колебаний с близкими частотами, называются биениями. 

П усть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω<<ω. Выберем начало отсчета так, чтобы начальные фазы обоих колебаний были равны нулю:    Складывая эти выражения и учитывая, что во втором сомножителе Δω/2<<ω, получим   (3) 

Результирующее колебание (3) можно считать как гармоническое с частотой ω , амплитуда А_σ которого изменяется по следующему периодическому закону:   (4)  Частота изменения А_σ в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений р авна разности частот складываемых колебаний:  П ериод биений:

2 ) Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:  [кг*м²/с]  Точка = полюс!!!!

 Билет №4

1 ) В общем случае, работа переменной силы, действующей на тело, движущееся по криволинейной траектории. Работа измеряется в Джоулях [Дж].

Р абота равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела. Это утверждение называют теоремой о кинетической энергии.

Кинетическая энергия тела массой m, движущегося со скоростью, равна работе, которую должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

2) Момент импульса материальной точки относительно точки O определяется векторным произведением , где   — радиус-вектор, проведенный из точки O,   — импульс материальной точки. Момент импульса материальной точки относительно неподвижной оси    равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса    не зависит от положения точки O на оси z. [кг*м²/с]

Билет №5

1 ) Уравнение свободных незатухающих колебаний:   (Вместо S писать X!!!!!) Решением этого дифференциального уравнения, в чем можно убедиться подстановкой, является функция:    

Гармоничным осциллятором называется физический объект, эволюция которого со временем описывается дифференциальным уравнением  , 

 

- Кинетическая энергия гармонического осциллятора задается выражением  .  - Потенциальная энергия гармонического осциллятора задается выражением 

.  - Обобщенный импульс, где q – обобщенная координата гармонического осциллятора

2 ) Моментом силы относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точ­ки О в точку А приложения силы, на силу F: [ Н*м]

З десь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы                                                    

где a— угол между r и F; r sina = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

Билет №6

1 ) При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами m опишет окружность соответствующих радиусов r; при этом объем будет иметь соответствующую линейную скорость v. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова: 

  где J_z - момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела 

Кинетическая энергия твердого тела, вращающегося отн. неподвижной оси =

2) Фаза колебаний — аргумент периодической функции или описывающей гармонический колебательный процесс ( — угловая частота, t— время, — начальная фаза колебаний, то есть фаза колебаний в начальный момент времени t = 0).

Фаза колебаний — величина, показывающая, какая часть колебания прошла с начала процесса. Фаза обычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода).

Билет №7

1) Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z. 

М онет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:    Используя формулу v_i = ωr_i, получим:  т. е.  

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение по времени:  т. е.   

2 ) Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела   к промежутку времени  , за который этот поворот произошел.

Угловая скорость выражается в радианах в секунду (рад/с). Билет №8

1 ) Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы. Положение центра масс определяется его радиус-вектором  

, где  - радиус-векторы точек, образующих систему.

Формулы, определяющие координаты центра тяжести:

Уравнение изменения импульса механической системы.

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

Закон сохранения импульса механической системы.

В замкнутой системе импульс сохраняется.

Другая формулировка: Суммарный импульс замкнутой системы остается постоянным по модулю и направлению, хотя импульс каждого из тел системы может изменяться.

Доказательство:

Рассмотрим механическую систему из N тел, массы и скорости которых соответсвенно равны m1, m2, ..., mN; V1, V2, ..., VN.

Запишем второй закон Ньютона для каждого из N тел механической системы:

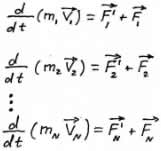
2 ) Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор   сонаправлен вектору  , при замедлен­ном — противонаправлен ему.  Угловое ускорение измеряется в рад/с.

Билет №9

1 ) Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами т и М, находящихся на расстоянии r одна от другой, равна

                                                           

г де G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е_p = 0) принят при r = ∞. Потенциальная энергия гравитационного взаимодействия тела массой т с Землей, где h – высота тела над поверхностью Земли, М₃ – масса Земли, R₃ – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

                                                    

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой т с Землей для малых высот h (h « R₃) равна

Е_p = m∙g∙h,

где   – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упругой деформации (пружины)

Н айдём работу, совершаемую при деформации упругой пружины.  Сила упругости Fупр = –kx, где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа dA = Fdx = –kxdx.  (Знак минус говорит о том, что работа совершена над пружиной). Тогда , т.е. A = U1 – U2. Примем: U2 = 0, U = U1, тогда  .

2 ) Полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

с оответственно величина   называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является (кг·м/с).

Импульс системы, на которую не действуют никакие внешние силы, сохраняется во времени:

Билет №10

1 ) I_c = kmR². Моменты инерции шара, диска и стержня

Ш ар:  k = 2/5,    Диск: k = 1/2,   

Сфера:   Обруч:  

       При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей через центр инерции, следует пользоваться теоремой о параллельном переносе осей, или теоремой Штейнера основным уравнением динамики поступательного движения:

       Момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс С тела, плюс произведение массы тела на квадрат расстояния между осями. 

2 ) Векторную сумму моментов импульсов   всех материальных точек системы называют моментом импульса (количества движения)   системы относительно точки О:

В екторы   и   взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому  . С учетом связи линейных и угловых величин:

и направлен вдоль оси вращения тела в ту же сторону, что и вектор  .

Т аким образом: [м²·кг·с⁻¹]

Билет №11

1) Процесс распространения колебаний в среде называется волной. Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной.  Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.

П рименим второй закон Ньютона и закон сложения сил к движению куска стержня, заключенного между двумя плоскостями x и х+ х. Масса этого куска равна р₀S₀ х, где р₀ и S₀ – соответственно плотность и сечение в отсутствие деформации. Пусть   – смещение центра тяжести рассматриваемого куска. Тогда:

с лева стоит произведение массы куска на ускорение д­­­2 /дt2 его центра тяжести, справа – результирующая внешних сил, действующая на кусок.

Разделим уравнение на S₀ :

Перейдя к пределу при  , получим уравнение:

 (2.8) справедливое в каждой точке стержня.

Подставляя в (2.8) соотношение (2.7), получим:

 

Вспомнив теперь формулу , содержащую определение дефор­мации, и подставив ее в (2.9), получаем:

Это — волновое уравнение. Оно указывает, что смещение распростра­няется по стержню в виде волн:

2) Моментом импульса системы относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z. 

М онет импульса системы относительно оси есть сумма моментов импульса отдельных частиц:    Используя формулу v_i = ωr_i, получим:  т. е.  

Таким образом, момент импульса системы относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение по времени: [м²·кг·с⁻¹] т. е.