
- •Математичний аналіз (другий семестр) Поняття функції кількох змінних.
- •Скорочені позначення
- •Поняття неперервності функції кількох змінних в точці та області.
- •Частинні похідні першого порядку.
- •Повний диференціал функції багатьох змінних. Інваріантність повного диференціала.
- •Модифікована таблиця невизначених інтегралів.
- •Інтегрування раціональних дробів з квадратичним знаменником.
- •Метод інтегрування по частинах
- •Обчислення інтегралів виду:
- •Обчислення інтегралів виду: , , ,
- •Обчислення інтегралів виду: ,
- •Поняття алгебраїчного дробу. Розклад алгебраїчних дробів на найпростіші.
- •Алгоритм розкладу правильного алгебраїчного дробу на суму найпростіших.
- •Інтегрування найпростіших алгебраїчних дробів.
- •Інтегрування деяких ірраціональностей.
- •Підстановки Ейлера.
- •Інтегрування біноміальних диференціалів.
- •Інтегрування деяких тригонометричних функцій. Інтеграли вигляду , де раціональна функція.
Алгоритм розкладу правильного алгебраїчного дробу на суму найпростіших.
Перший крок: визначити структуру розкладу .
Для цього треба
розкласти поліном
на співмножники вигляду
![]() ,
де
,
де
![]() - дійсні корені рівняння
- дійсні корені рівняння
![]() ,
вирази
,
вирази
![]() ,
такі що відповідне квадратне рівняння
немає коренів.
,
такі що відповідне квадратне рівняння
немає коренів.
Цей розклад називають розкладом знаменника правильного алгебраїчного дробу на лінійні та квадратичні співмножники, які не мають дійсних коренів.
Структура цього розкладу дозволяє визначити структуру розкладу правильного алгебраїчного дробу наступним чином:
виразу
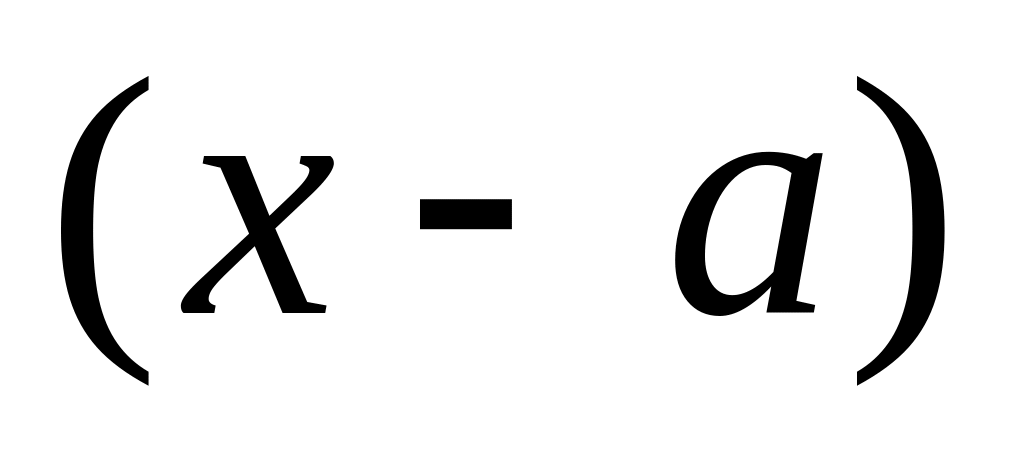 в розкладі
,
відповідає алгебраїчний дріб вигляду
в розкладі
,
відповідає алгебраїчний дріб вигляду
виразу
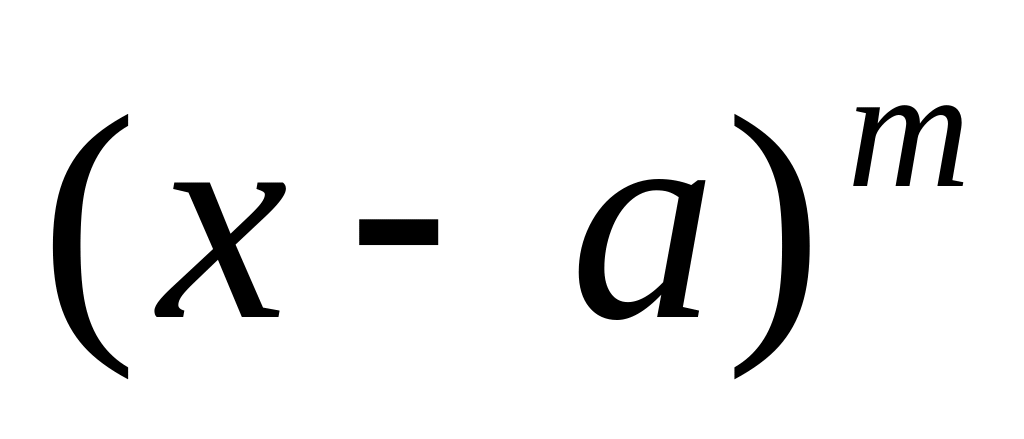 в розкладі
,
де
в розкладі
,
де
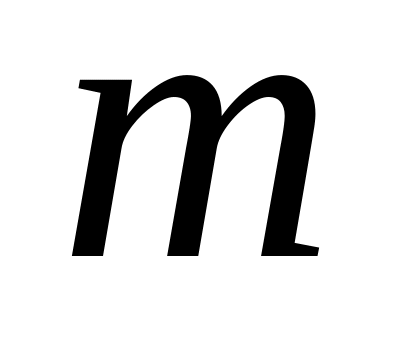 натуральне число більше 1, відповідає
сума алгебраїчних дробів вигляду
натуральне число більше 1, відповідає
сума алгебраїчних дробів вигляду
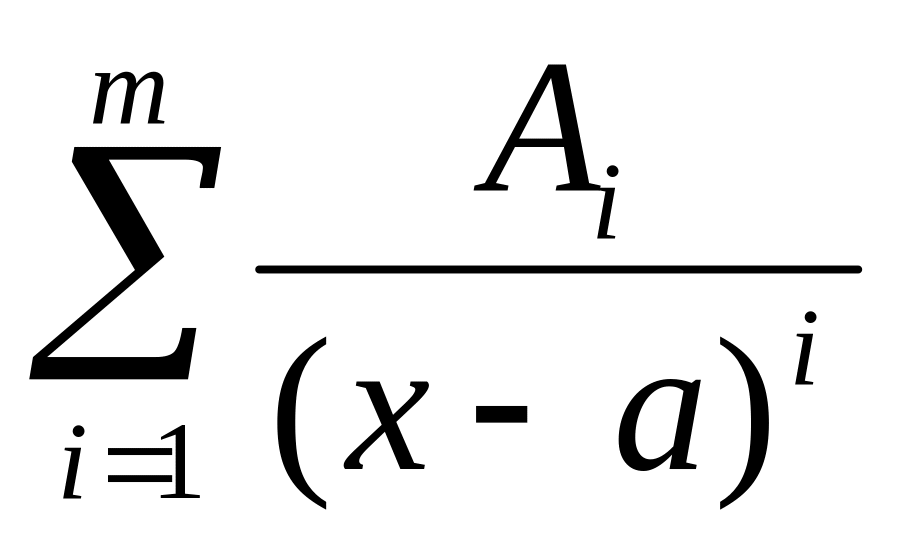 .
.виразу
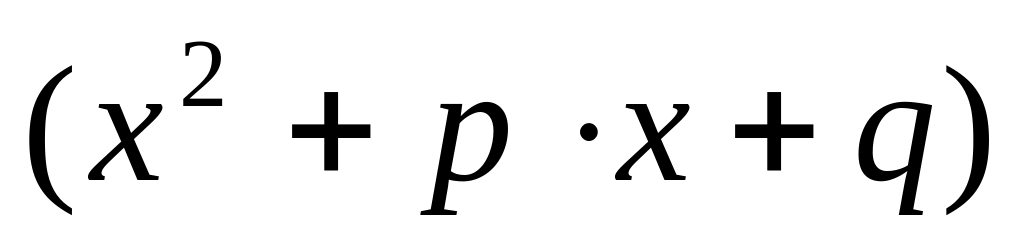 в розкладі
,
відповідає алгебраїчний дріб вигляду
в розкладі
,
відповідає алгебраїчний дріб вигляду
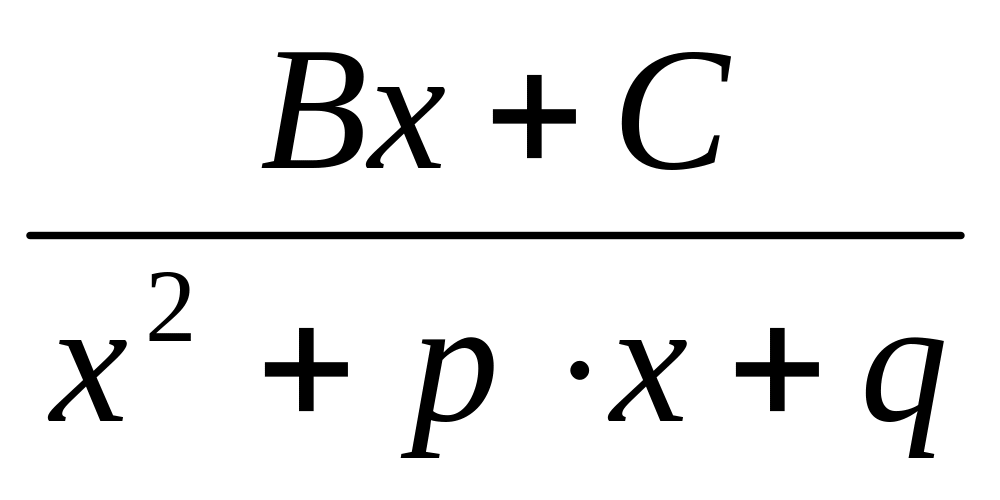
виразу
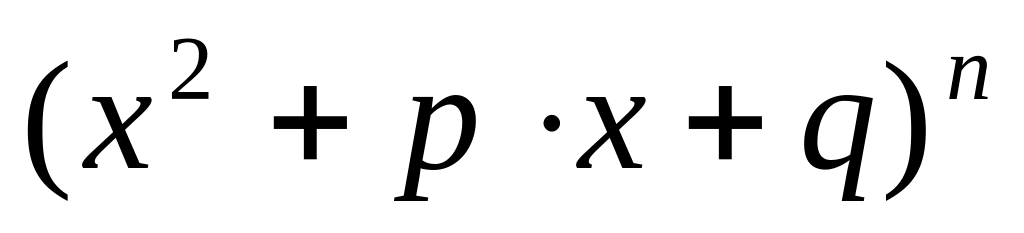 в розкладі
,
де n
натуральне число більше 1, відповідає
сума алгебраїчних дробів вигляду
в розкладі
,
де n
натуральне число більше 1, відповідає
сума алгебраїчних дробів вигляду
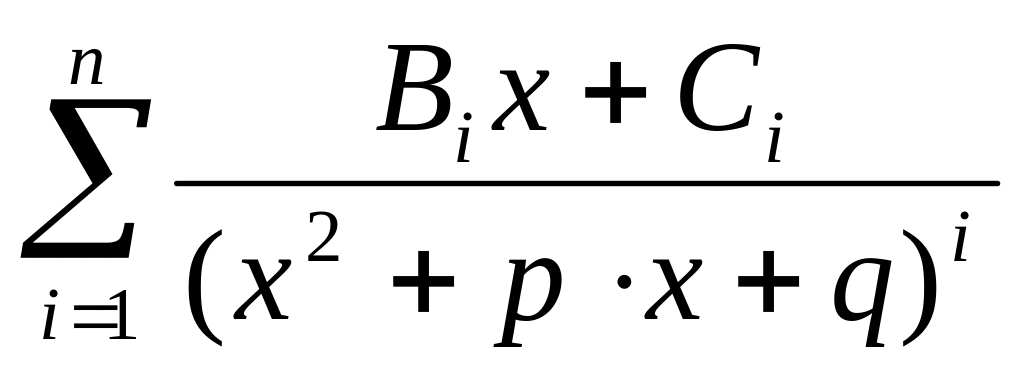
Другий крок:
На основі першого кроку записати розклад даного правильного алгебраїчного дробу на суму найпростіших з невизначеними коефіцієнтами.
Знайти суму отриманих правильних алгебраїчних дробів з невизначеними коефіцієнтами у вигляді дробу
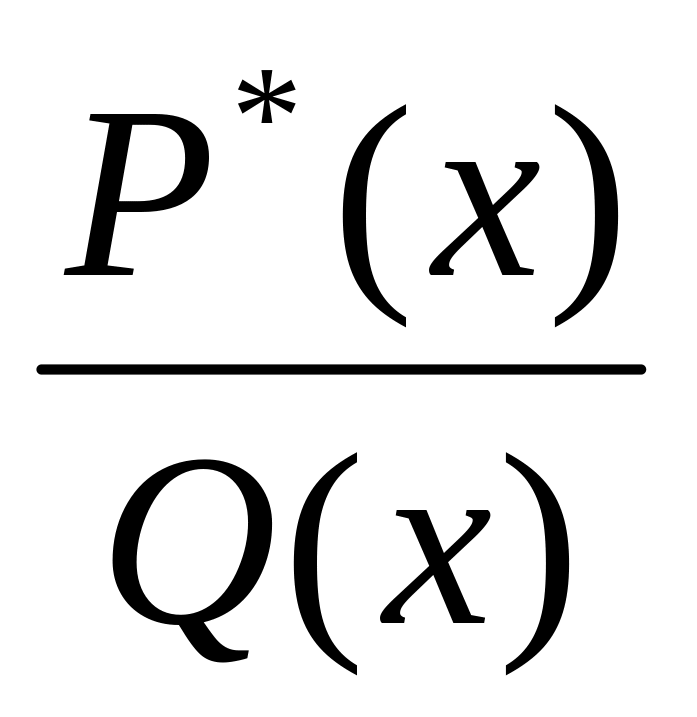 ,
де
,
де
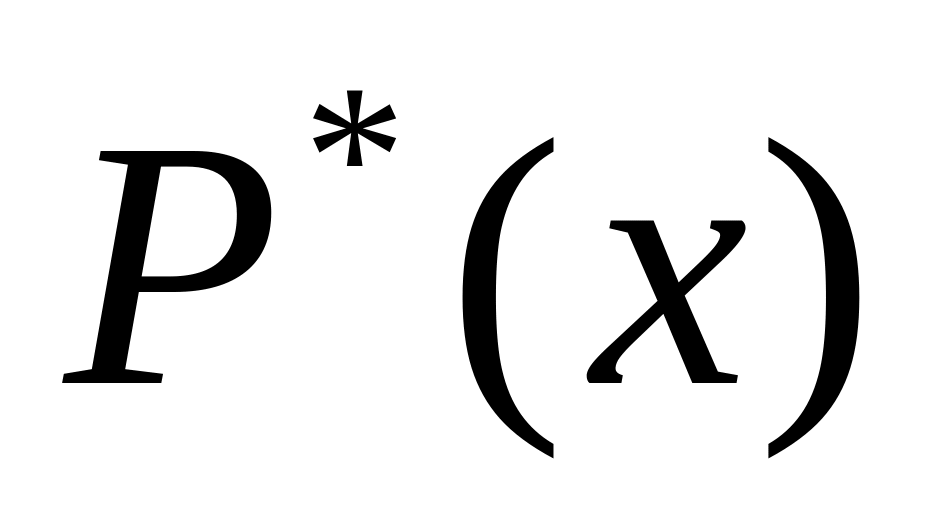 поліном того ж степеня що і
,
але з невизначеними коефіцієнтами.
поліном того ж степеня що і
,
але з невизначеними коефіцієнтами.Прирівняти коефіцієнти при однакових степенях поліномів і . В результаті прирівнювання цих коефіцієнтів будемо мати систему лінійних алгебраїчних рівнянь для визначення невизначених коефіцієнтів.
Інтегрування найпростіших алгебраїчних дробів.
Нехай дано алгебраїчний дріб тоді
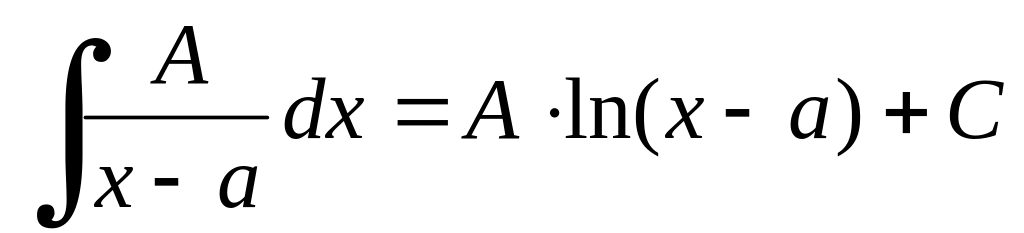 .
.Нехай дано алгебраїчний дріб , де натуральне число більше 1, тоді
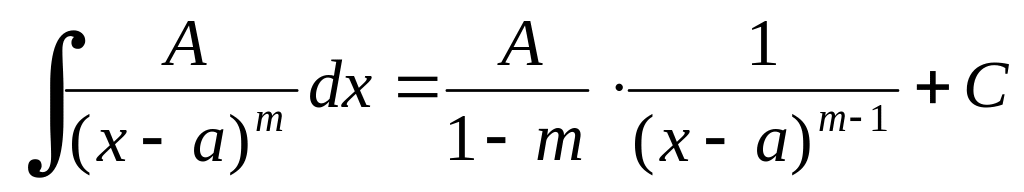
Нехай дано
алгебраїчний дріб
![]() ,
причому квадратне рівняння
немає коренів, що справедливо коли
,
причому квадратне рівняння
немає коренів, що справедливо коли
![]() ,
тоді інтеграл
,
тоді інтеграл
![]()
Нехай дано алгебраїчний дріб , причому квадратне рівняння немає коренів, тоді на першому кроці знаходження інтеграла
![]()
Рекомендована
підстановка
![]()
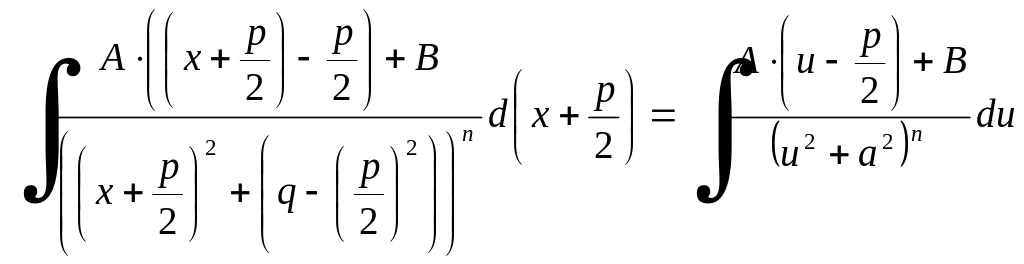
Інтеграл
![]() ,
обчислюється за допомогою рекурентної
формули:
,
обчислюється за допомогою рекурентної
формули:
![]()
![]()
Інтегрування деяких ірраціональностей.
Інтеграли вигляду
![]() ,
де
- раціональна функція,
,
де
- раціональна функція,
![]() - раціональні числа зводяться до
інтегралів від раціональної функції
за допомогою підстановки
- раціональні числа зводяться до
інтегралів від раціональної функції
за допомогою підстановки
![]() ,
де
,
де
![]() - спільний
знаменник
дробів
.
- спільний
знаменник
дробів
.
Інтеграли вигляду
![]() ,
де
- раціональна функція,
- раціональні числа зводяться до
інтегралів від раціональної функції
за допомогою підстановки
,
де
- раціональна функція,
- раціональні числа зводяться до
інтегралів від раціональної функції
за допомогою підстановки
![]() ,
де
- спільний
знаменник
дробів
.
,
де
- спільний
знаменник
дробів
.
Підстановки Ейлера.
Інтеграли вигляду
![]() зводяться до інтегралів від раціональної
функції за допомогою однієї з трьох
підстановок Ейлера:
зводяться до інтегралів від раціональної
функції за допомогою однієї з трьох
підстановок Ейлера:
Якщо виконується умова
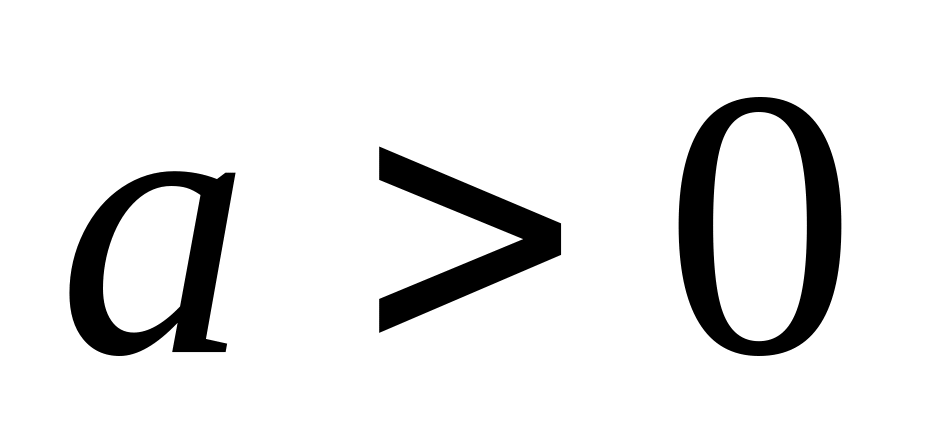 то рекомендується перша
підстановка Ейлера:
то рекомендується перша
підстановка Ейлера:
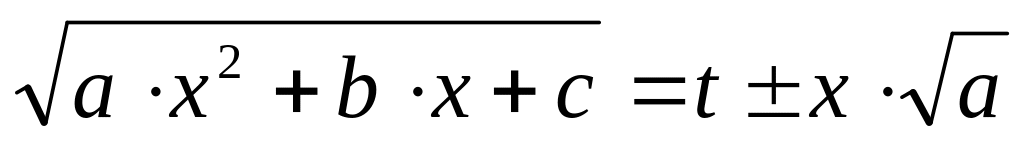
Якщо виконується умова
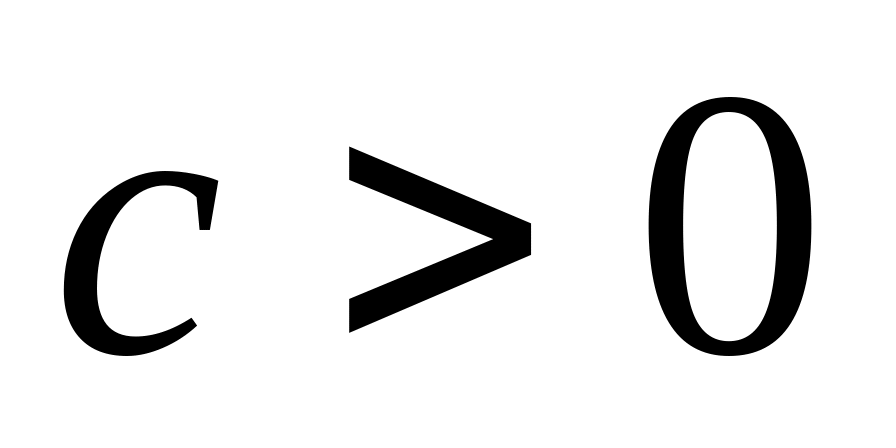 то рекомендується друга
підстановка Ейлера
:
то рекомендується друга
підстановка Ейлера
:
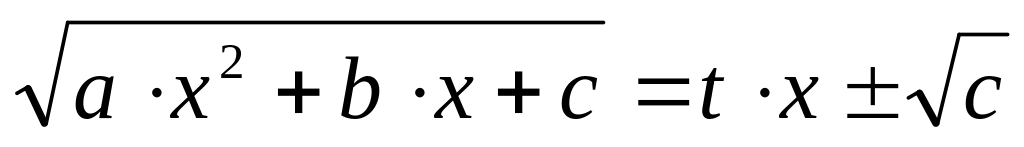
Якщо
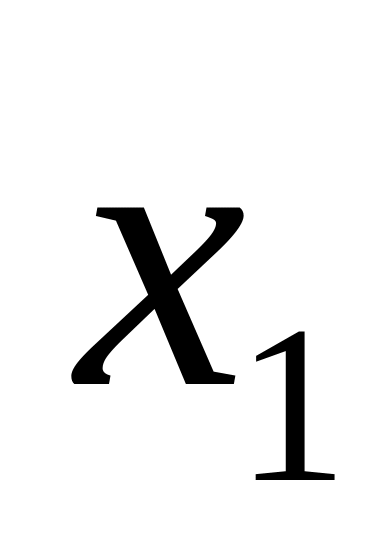 та
та
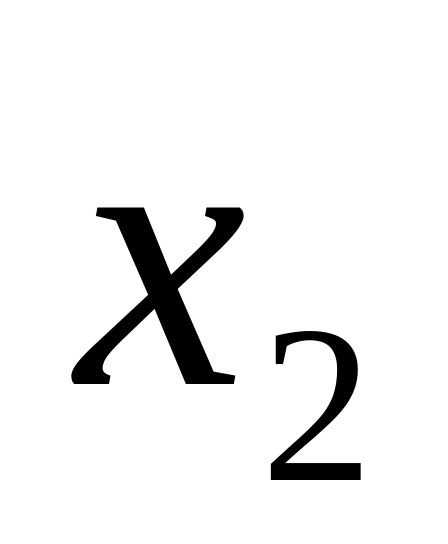 корені квадратного рівняння
корені квадратного рівняння
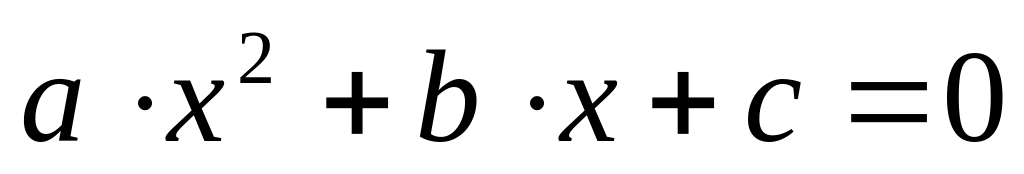 то рекомендується третя підстановка Ейлера :
то рекомендується третя підстановка Ейлера :
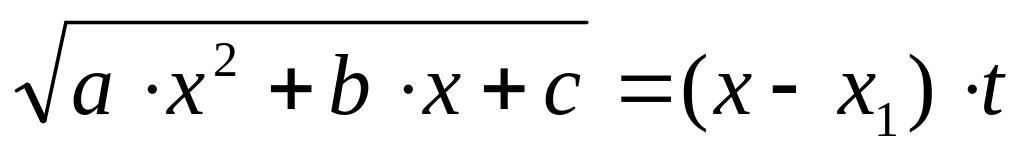 або
або
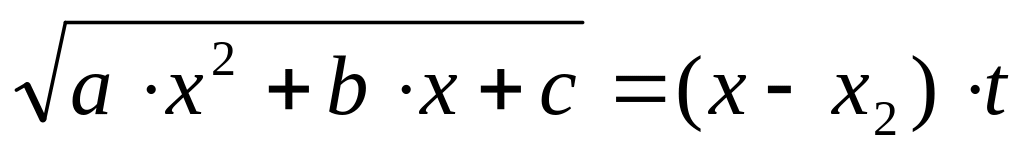
Інтегрування біноміальних диференціалів.
Біноміальним
диференціалом
називається вираз
![]() ,
де
,
,
,
де
,
,
![]() - раціональні числа.
- раціональні числа.
Інтеграл від
біноміального диференціала
![]() зводиться до інтеграла від раціональної
функції в наступних трьох випадках:
зводиться до інтеграла від раціональної
функції в наступних трьох випадках:
Випадок 1:
Показник степеня
- ціле число. Тоді інтеграл від біноміального
диференціала зводиться до інтеграла
від раціональної функції за допомогою
підстановки
![]() ,
де
,
де
![]() спільний знаменник дробів
та
.
спільний знаменник дробів
та
.
Випадок 2:
Число
![]() ціле. Тоді інтеграл від біноміального
диференціала зводиться до інтеграла
від раціональної функції за допомогою
підстановки
ціле. Тоді інтеграл від біноміального
диференціала зводиться до інтеграла
від раціональної функції за допомогою
підстановки
![]() де
де
![]() - знаменник дробу
.
- знаменник дробу
.
Випадок 3:
Число
![]() ціле. Тоді інтеграл від біноміального
диференціала зводиться до інтеграла
від раціональної функції за допомогою
підстановки
ціле. Тоді інтеграл від біноміального
диференціала зводиться до інтеграла
від раціональної функції за допомогою
підстановки
![]() де
- знаменник дробу
.
де
- знаменник дробу
.
