
- •Математичний аналіз (другий семестр) Поняття функції кількох змінних.
- •Скорочені позначення
- •Поняття неперервності функції кількох змінних в точці та області.
- •Частинні похідні першого порядку.
- •Повний диференціал функції багатьох змінних. Інваріантність повного диференціала.
- •Модифікована таблиця невизначених інтегралів.
- •Інтегрування раціональних дробів з квадратичним знаменником.
- •Метод інтегрування по частинах
- •Обчислення інтегралів виду:
- •Обчислення інтегралів виду: , , ,
- •Обчислення інтегралів виду: ,
- •Поняття алгебраїчного дробу. Розклад алгебраїчних дробів на найпростіші.
- •Алгоритм розкладу правильного алгебраїчного дробу на суму найпростіших.
- •Інтегрування найпростіших алгебраїчних дробів.
- •Інтегрування деяких ірраціональностей.
- •Підстановки Ейлера.
- •Інтегрування біноміальних диференціалів.
- •Інтегрування деяких тригонометричних функцій. Інтеграли вигляду , де раціональна функція.
Урманчев В.І.
Математичний аналіз (другий семестр) Поняття функції кількох змінних.
Нехай
![]() та
та
![]() довільні множини.
довільні множини.
Функцією визначеною на множині називають правило яке елементу множини співставляє один і тільки один елемент множини .
Функції мають імена в якості яких вибирають букви латинського алфавіту (як великі так і малі).
Найбільш вживаними
буквами є
![]() та
та
![]() .
.
Множину називають областю визначення функції .
Елементи множини називають аргументами (або незалежними змінними) функції .
Множину називають множиною значень функції .
Значення функції
коли її аргумент дорівнює
![]() позначають
позначають
![]() .
.
Декартовим
добутком множин
![]() та
та
![]() називається множина
називається множина
![]() всіх впорядкованих пар
всіх впорядкованих пар
![]() ,
де
,
де
![]() ,
,
![]() .
Позначення:
.
Позначення:
![]() .
.
Нехай
![]() довільна множина.
довільна множина.
Множина
![]() називається декартовим
степенем
множини
.
називається декартовим
степенем
множини
.
Множину
![]() називають n-вимірним
простором.
називають n-вимірним
простором.
Його елементи
називають n-вимірними
векторами і позначають
![]() .
.
Функції, областю значень яких є підмножини , називаються функціями від n змінних. Якщо n не є суттєвим такі функції називають функціями багатьох змінних.
Функції багатьох
змінних, областю означення яких є
підмножини
![]() ,
називаються скалярними
функціями багатьох змінних.
,
називаються скалярними
функціями багатьох змінних.
Позначення
![]() ,
або
,
або
![]() .
.
Функції, областю
значень яких є підмножини
![]() ,
називаються вектор-функціями
багатьох змінних.
,
називаються вектор-функціями
багатьох змінних.
Позначення
![]() або
або
![]() .
.
Скорочені позначення
![]() -
для кожного
-
для кожного
![]() -
існує
-
існує
: - таке що
Поняття неперервності функції кількох змінних в точці та області.
Нехай
довільний n-вимірний
вектор, число
![]() називають нормою вектора
називають нормою вектора
![]() .
.
Говорять, що
n-вимірний
вектор
прямує до n-вимірного
вектора
![]() ,
якщо
,
якщо
![]() ,
,
![]() .
.
Скорочене позначення
![]() .
.
Число
![]() називається границею
функції
називається границею
функції
![]() при
,
що прямує до
при
,
що прямує до
![]() якщо для кожного
якщо для кожного
![]() існує таке число
існує таке число
![]() що для всіх чисел
що для всіх чисел
![]() які задовольняють нерівність
які задовольняють нерівність
![]() виконується нерівність
виконується нерівність
![]() .
.
Позначення
![]() .
.
Якщо розмірність невелика замість векторних позначень всі набори .
Наприклад для
![]() пишуть
пишуть
![]() .
.
Означення границі
функції записане за допомогою скорочених
позначень:
![]() .
.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() якщо
якщо
![]() .
.
Точка називається точкою розриву функції якщо ця точка визначена в деякому околі точки , але в самій точці непевність порушується.
Частинні похідні першого порядку.
Частковою
похідною
від функції
![]() по аргументу
по аргументу
![]() називається похідна від цієї функції
по
при фіксованих
називається похідна від цієї функції
по
при фіксованих
![]() ,
де
,
де
![]() .
.
Позначення
![]() .
.
Наприклад:
Повний диференціал функції багатьох змінних. Інваріантність повного диференціала.
Нехай
,
![]() прирости аргументів
прирости аргументів
![]() ,
,
![]() відповідний приріст функції
відповідний приріст функції
![]() ,
тоді
,
тоді
![]() ,
причому точність цієї формули зростає
при
,
причому точність цієї формули зростає
при
![]() .
.
Розглядаючи границі
можна отримати формальний
вираз
![]() .
.
Цей вираз називають повним диференціалом функції .
Формула для повного диференціала залишається в силі, якщо аргументи функції замінити функціями будь яких інших аргументів - в цьому полягає властивість інваріантності повного диференціала.
Властивість інваріантності повного диференціала використовується при диференціюванні складних та неявних функцій багатьох аргументів.
Диференціювання складних функцій багатьох аргументів.
Нехай
,
![]() .
.
Треба знайти
![]() .
.
![]()
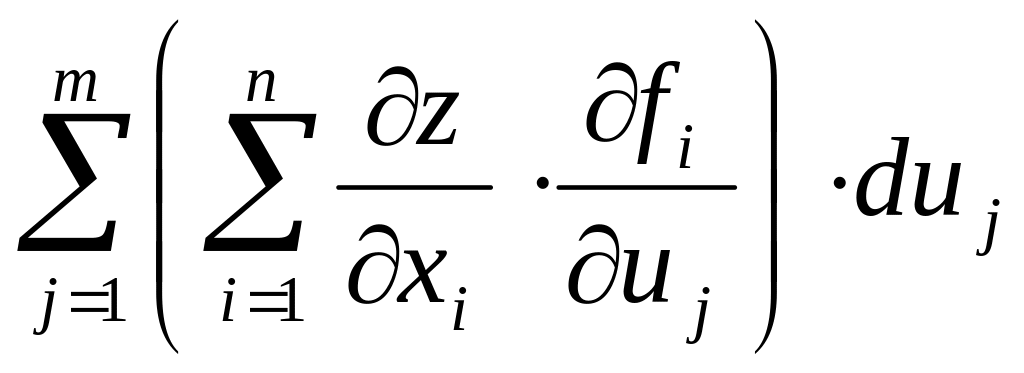
З інваріантності
повного диференціала
![]()
Таким чином
![]()
Отриману формулу
називають формулою для часткової
похідної по аргументу
![]() від складної функції багатьох аргументів.
від складної функції багатьох аргументів.
Приклади обчислення
Диференціювання неявних функцій багатьох аргументів.
Нехай дана функція
![]() і нехай функція
і нехай функція
![]() задається неявною формулою
задається неявною формулою
![]() .
.
Треба знайти
![]() .
.
![]()
![]()
![]()
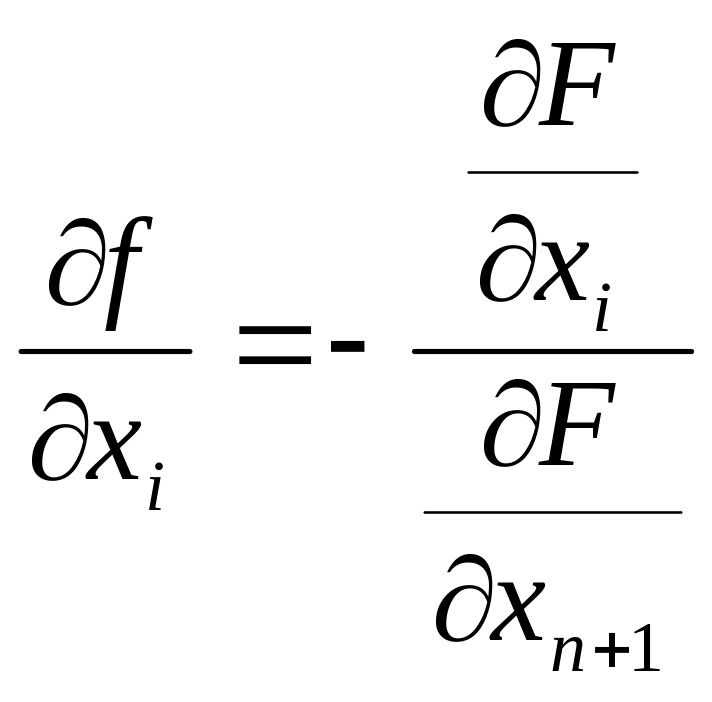
Приклади обчислення
Поняття градієнту. Похідна функції в даному напрямку.
Градієнтом
функції
,
називається вектор
![]()
Похідною функції в напрямку називають число
![]() .
.
Наприклад:
Частинні похідні вищих порядків.
Частковою похідною m-го порядку від функції по аргументу називається m-та похідна від цієї функції по при фіксованих , де .
Позначення
![]() .
.
Наприклад:
Можна розглядати
композиції часткових похідних різних
порядків по різним аргументам наприклад
:
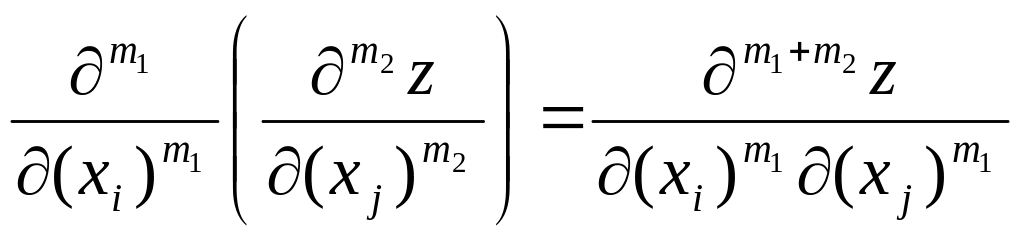 .
.
Наприклад:
Найбільш загальний вигляд такої композиції
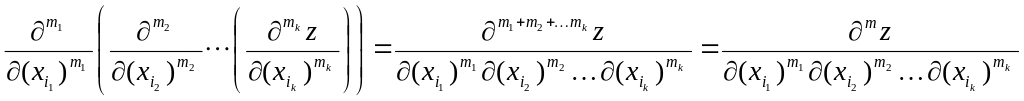
де
![]()
Такі композиції називаються мішаними похідними m-го порядку.
Приклади обчислення мішаних похідних:
Безумовні та умовні екстремуми.
Задача на екстремум без обмежень
Нехай
![]() .
.
Задачею
нелінійного програмування без обмежень
називається оптимізаційна задача
![]() ,
де
означає один з варіантів
,
де
означає один з варіантів
![]() ,
або
,
або
![]() .
.
Алгоритм розв’язку задачі нелінійного програмування без обмежень
![]()
![]()
Нехай
![]() - розв’язок цієї системи.
- розв’язок цієї системи.
Додатньо та від’ємно визначені матриці. Критерій Сильвестра
Нехай
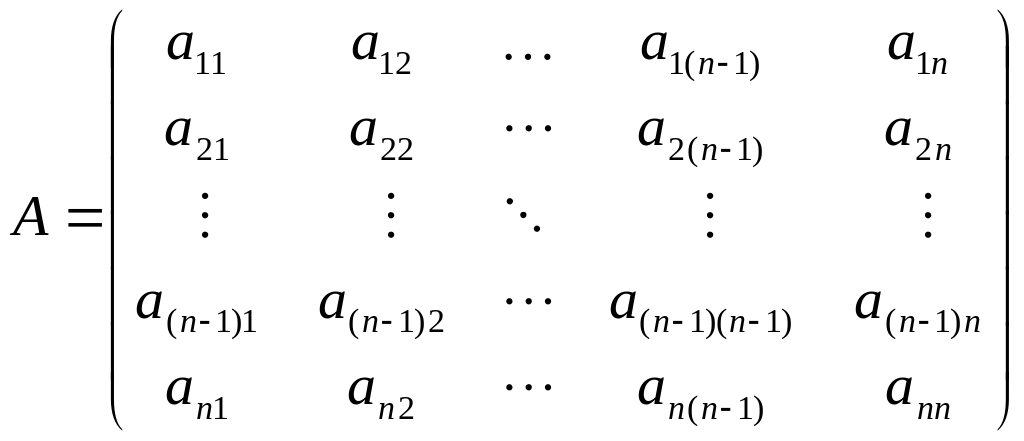 ,
,
![]() - скалярний
добуток в
.
- скалярний
добуток в
.
Матриця
називається додатньо
визначеною
якщо
![]() ,
,
![]()
![]()
Матриця
називається від’ємно
визначеною
якщо
,
![]()
Головними мінорами матриці називаються числа
![]()
![]()
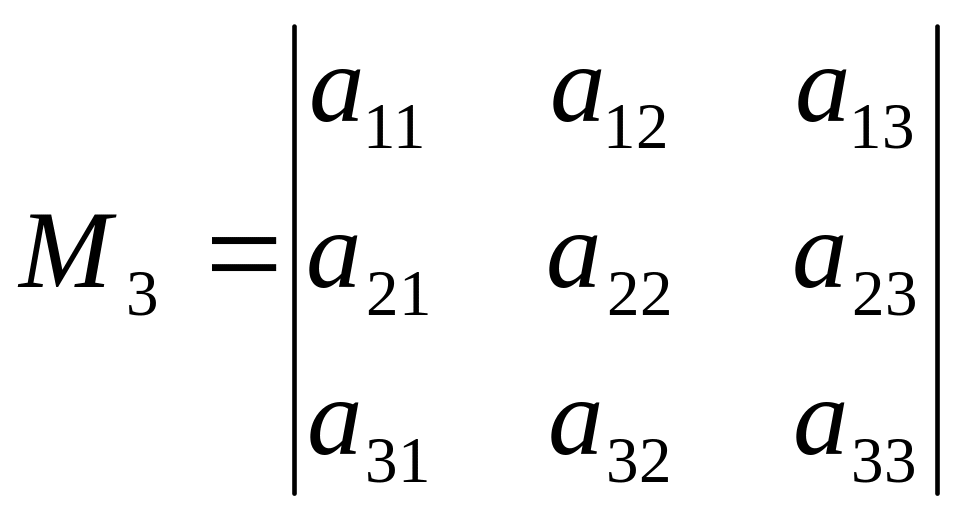
![]()
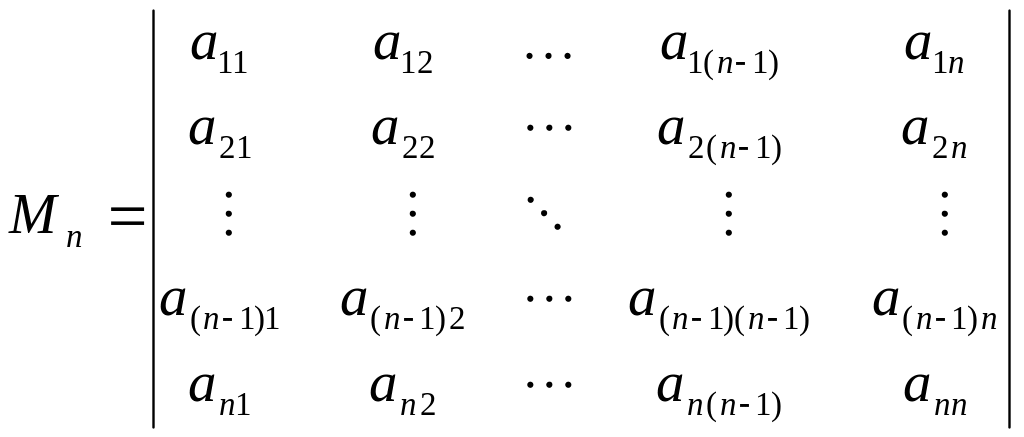
Теорема (критерій Сільвестра) Матриця є
додатньо визначеною тоді і тільки тоді, коли для всіх
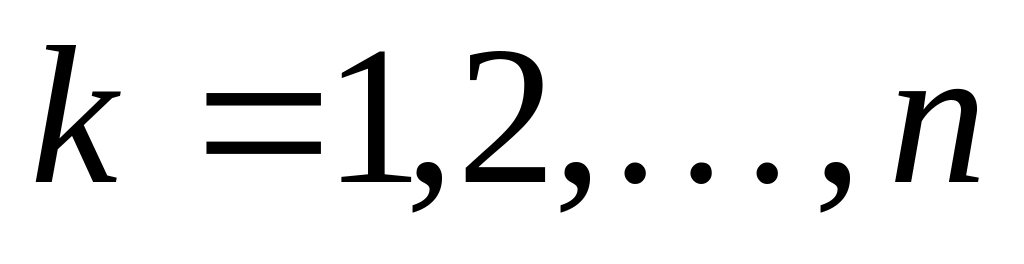
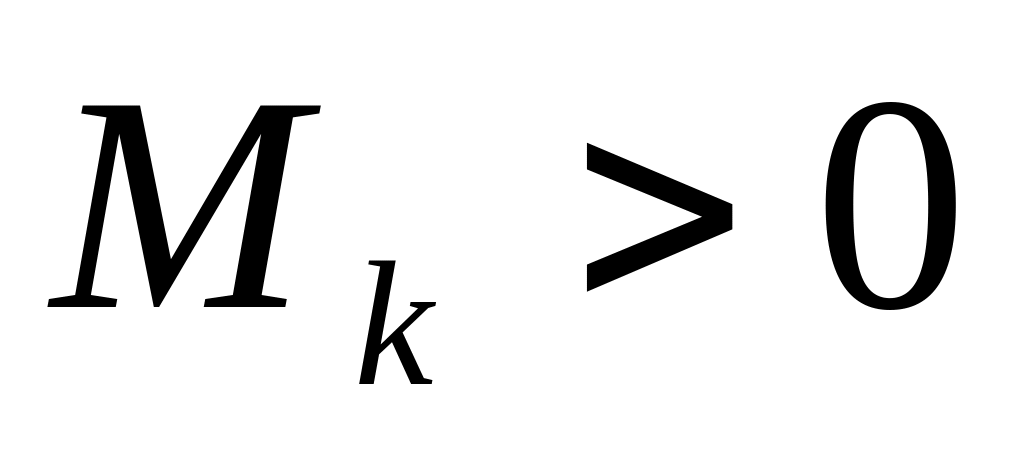
від’ємно визначеною тоді і тільки тоді, коли для всіх
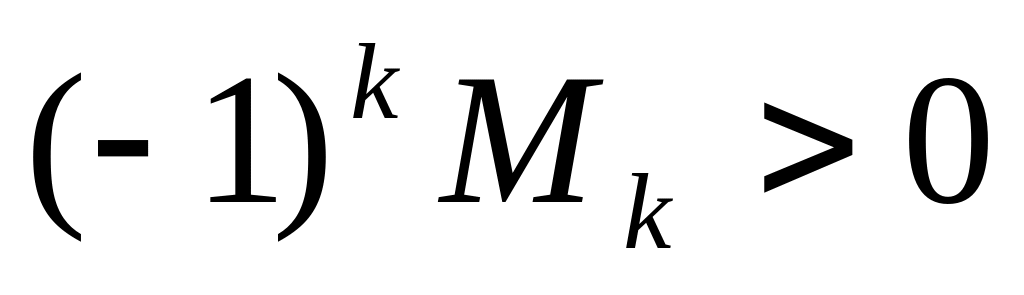 .
.
Приклади.
Нехай
![]()
Оскільки
![]() ,
,
![]() то за критерієм Сильвестра матриця А
додатньо визначена.
то за критерієм Сильвестра матриця А
додатньо визначена.
Введемо у розгляд
матрицю
![]() елементи якої визначається формулою
елементи якої визначається формулою![]() :
:
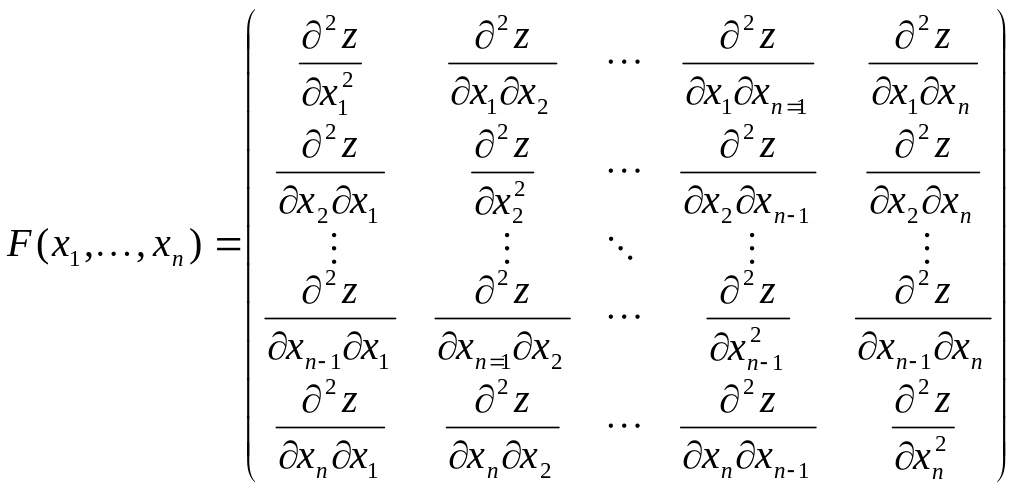
Якщо матриця
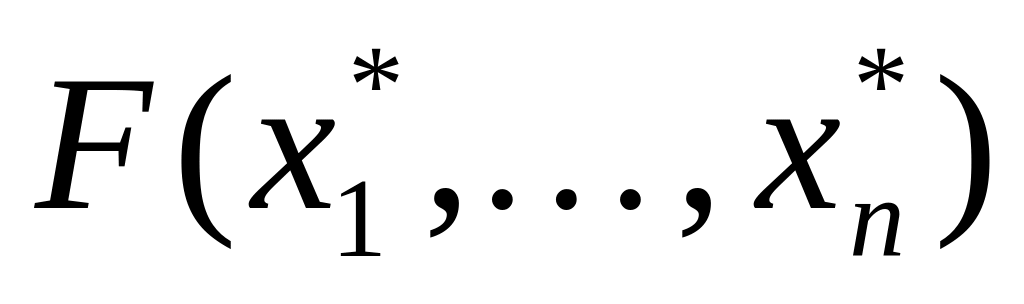 додатньо визначена то
є точкою мінімуму.
додатньо визначена то
є точкою мінімуму.Якщо матриця від’ємно визначена то є точкою максимуму.
Якщо матриця не є ні додатньо визначеною ні від’ємно визначеною то не є ні точкою мінімуму, ні точкою максимуму.
![]()
Нехай
![]() розв’язок цієї системи, тоді
розв’язок цієї системи, тоді
Якщо
![]() ,
,
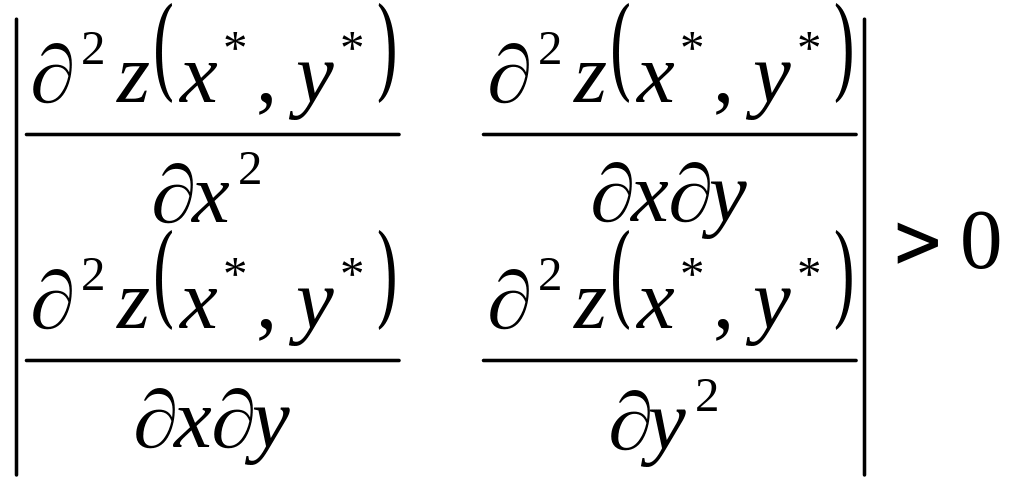 то
є точкою мінімуму.
то
є точкою мінімуму.
Якщо
![]() ,
то
є точкою максимуму.
,
то
є точкою максимуму.
Якщо
![]() ,
,
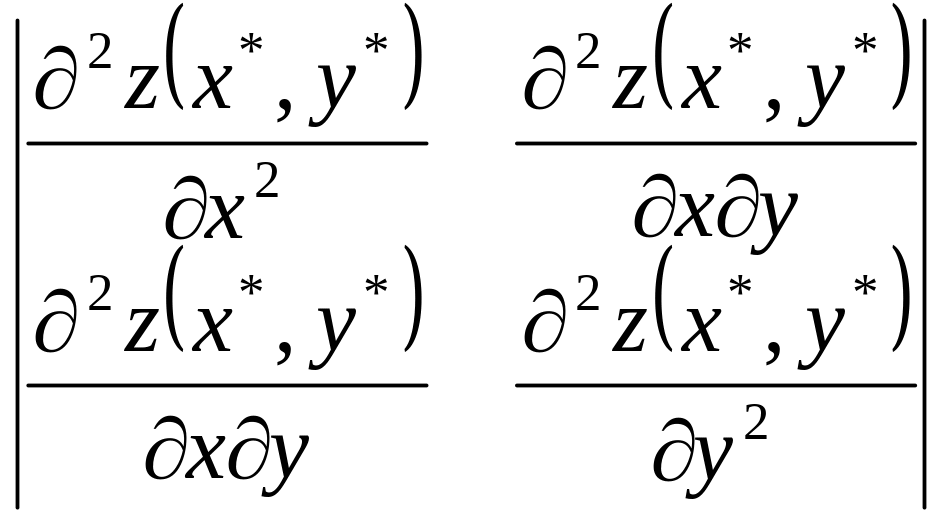 то
є сідловою точкою .
то
є сідловою точкою .
Задача на екстремум з обмеженнями
Нехай .
Задачею нелінійного програмування з обмеженнями називається оптимізаційна задача , де означає один з варіантів , або .
При додаткових умовах
Наближенні обчислення.
Інтегральне числення.
Невизначений інтеграл.
Поняття первісної функції та невизначеного інтеграла.
Функція
![]() називається первісною
для функції
називається первісною
для функції
![]() якщо
якщо
![]() .
.
Оскільки похідна від константи дорівнює нулю то для заданої функції існує нескінченна кількість первісних які відрізняються одна від одної на константу.
Вираз для сукупності
всіх первісних для функції
називається невизначеним інтегралом
для цієї функції і позначається так:
![]()
Властивості невизначеного інтеграла.
Таблиця найпростіших інтегралів.
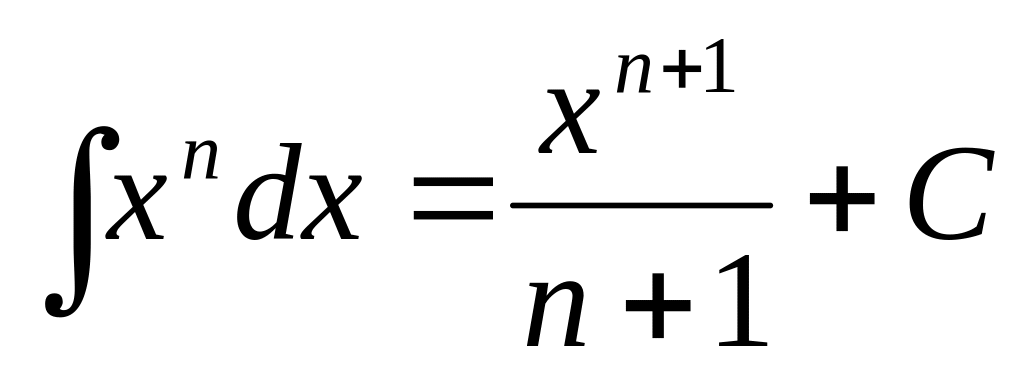 ,
,
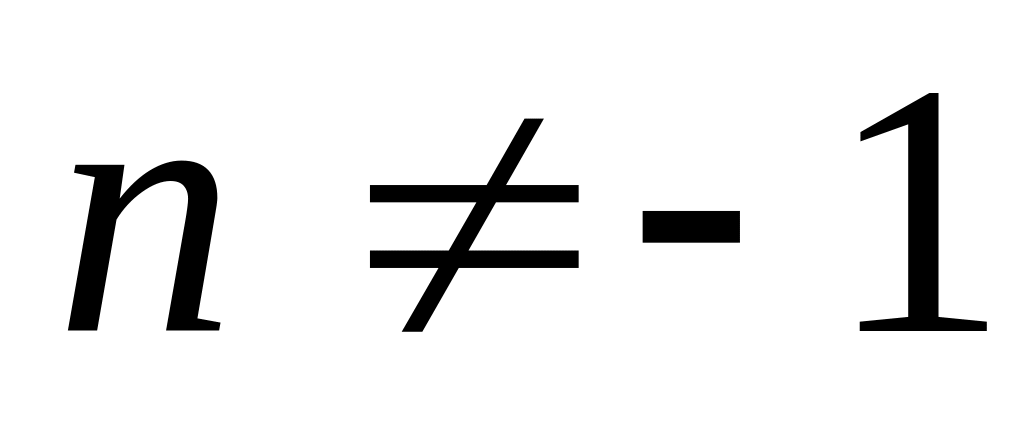
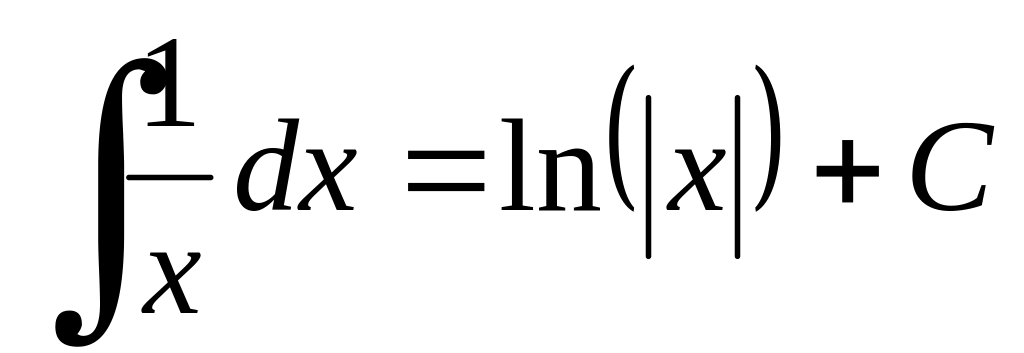
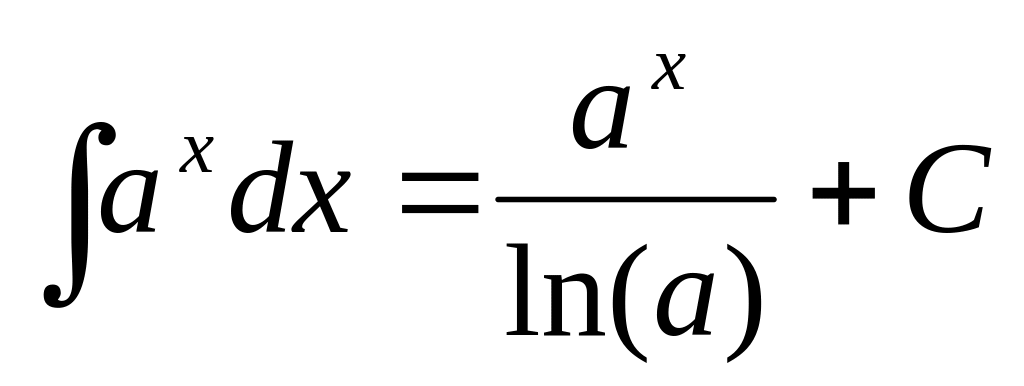 ,
частковий випадок
,
частковий випадок
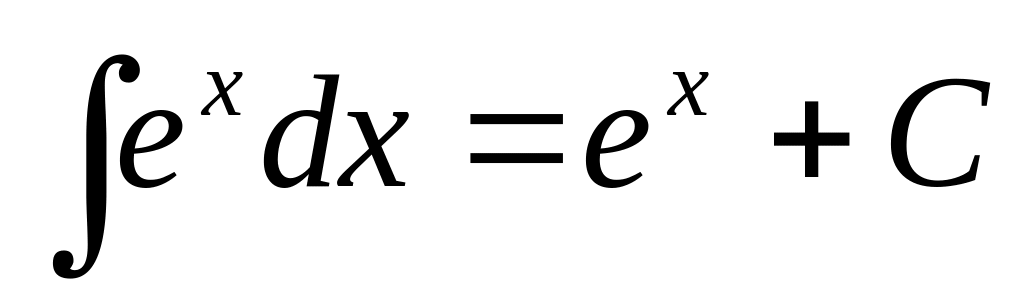
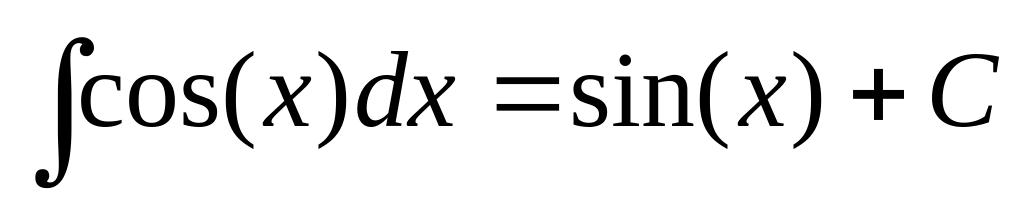
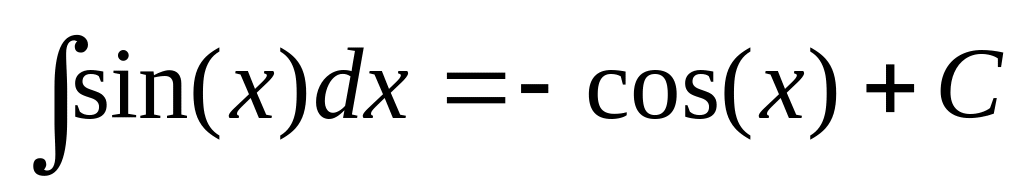
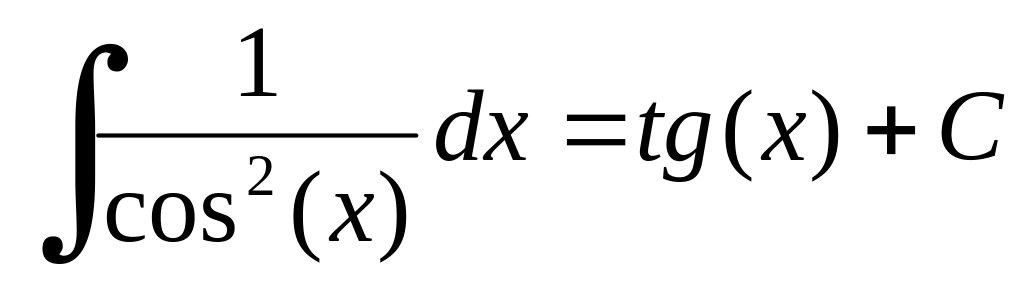
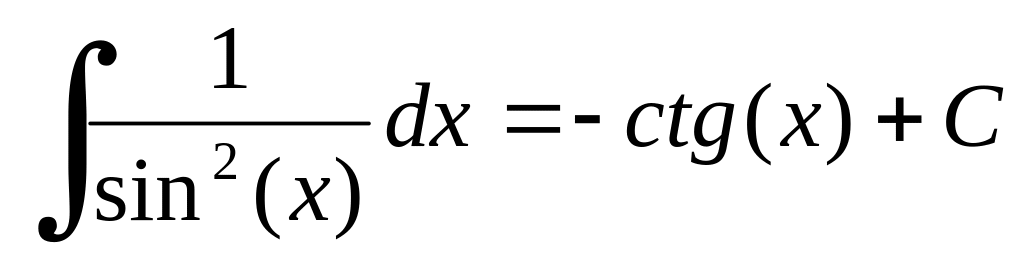
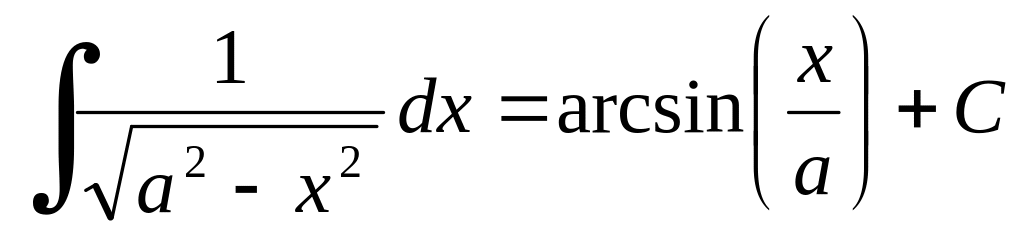
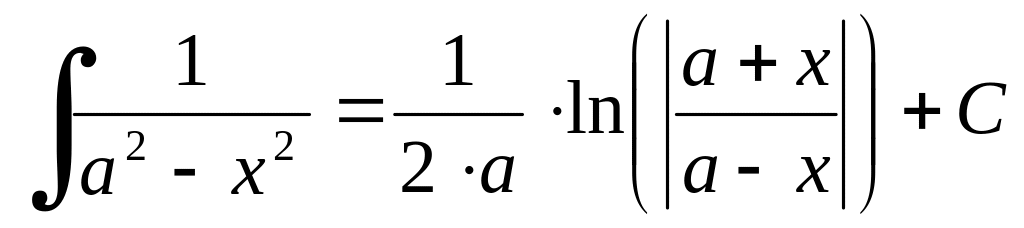
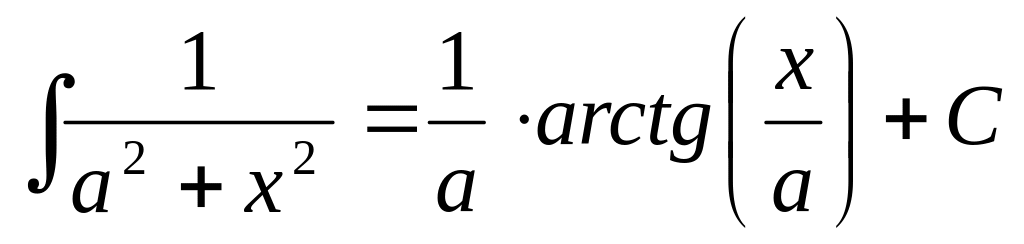
Інтегрування методом підстановки.
В основі інтегрування методом підстановки (або методом заміни змінної) лежить властивість інваріантності формул інтегрування, яке полягає в наступному:
Якщо
то
![]()
де
![]() - довільна диференційована функція від
.
- довільна диференційована функція від
.
Заміна змінної в невизначеному інтегралі робиться за допомогою підстановок двох типів:
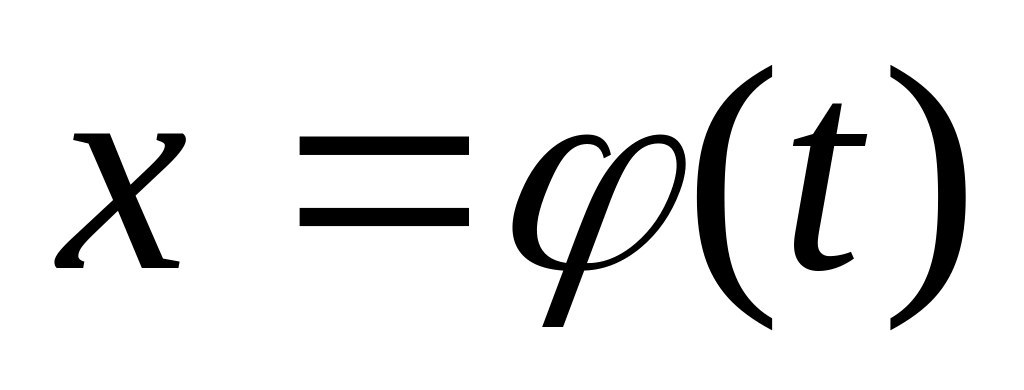 де
де
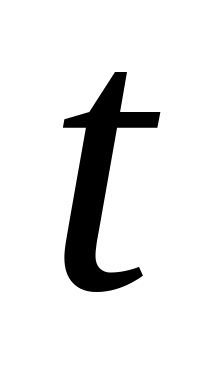 нова змінна, а
нова змінна, а
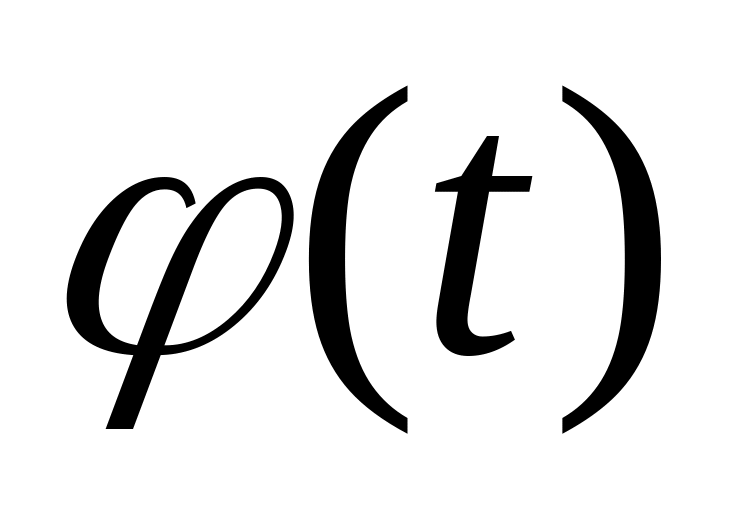 неперервно диференційована функція.
В
цьому випадку формула заміни змінної
неперервно диференційована функція.
В
цьому випадку формула заміни змінної
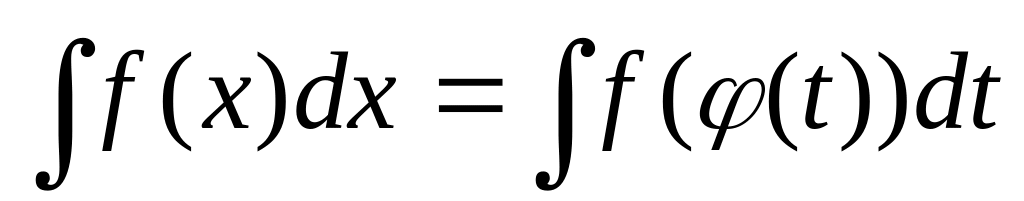 .
Функцію
вибирають таким чином щоб права частина
формули мала більш зручний для
інтегрування вигляд.
.
Функцію
вибирають таким чином щоб права частина
формули мала більш зручний для
інтегрування вигляд.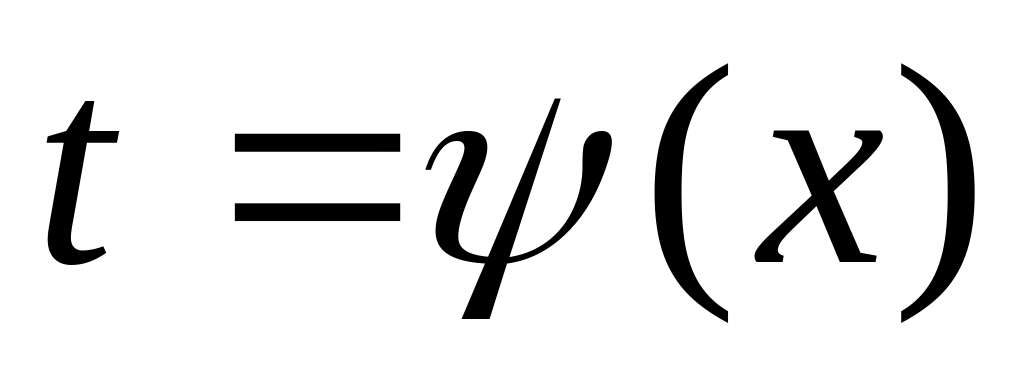 ,
де
нова змінна. В цьому випадку
представляють у вигляді
,
де
нова змінна. В цьому випадку
представляють у вигляді
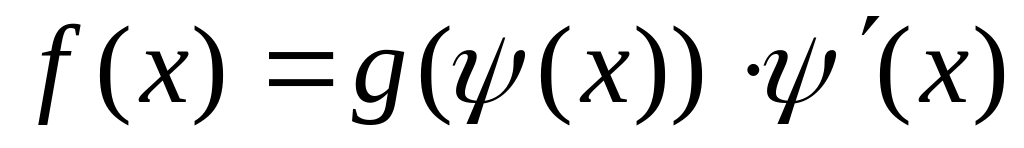 і формула заміни змінної
буде мати вигляд:
і формула заміни змінної
буде мати вигляд:
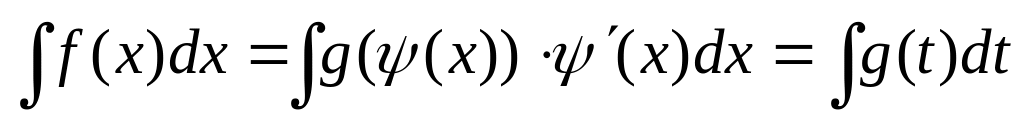 .
Функції
.
Функції
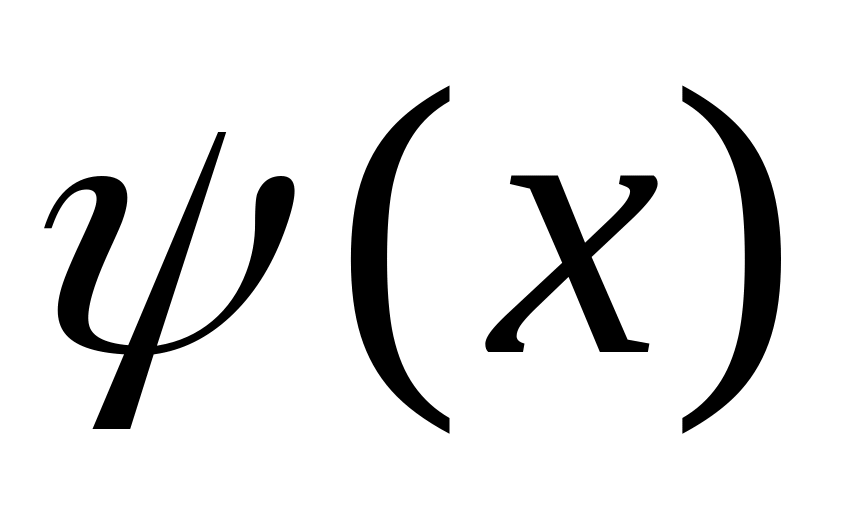 та
та
 вибирають таким чином щоб права частина
формули мала більш зручний для
інтегрування вигляд.
вибирають таким чином щоб права частина
формули мала більш зручний для
інтегрування вигляд.
Важливі часткові випадки:
Нехай тоді
![]()
![]()
![]()
