Тема 10. Статистические методы изучения взаимосвязей

Цель занятия: Освоить методику применения статистических методов для изучения взаимосвязей социально-экономических явлений.

Методические указания. Задача 1. Охарактеризуйте зависимость урожайности зерновых от качества почвы (табл. 259), рассчитав параметры нижеследующих функций: а) линейной, б) степенной, в) экспоненты, г) показательной, д) равносторонней гиперболы, е) обратной и т.д. Определите показатели тесноты связи для каждой модели, оценив каждую из них по показателю детерминации, F-критерию Фишера, ошибку апроксимации и выбрать наилучшую из них. Для расчетов используйте программы Statgraphics, статистические функции ЛИНЕЙН, ЛГРФПРИБЛ в MS Excel, инструмент анализа данных Регрессия и т.д.

Решение: для определения формы связи между урожайностью зерновых культур и качеством почвы построим график (рис. 29). На оси абсцисс нанесем значение независимой переменной (качество почвы), на оси ординат - зависимой (урожайность).

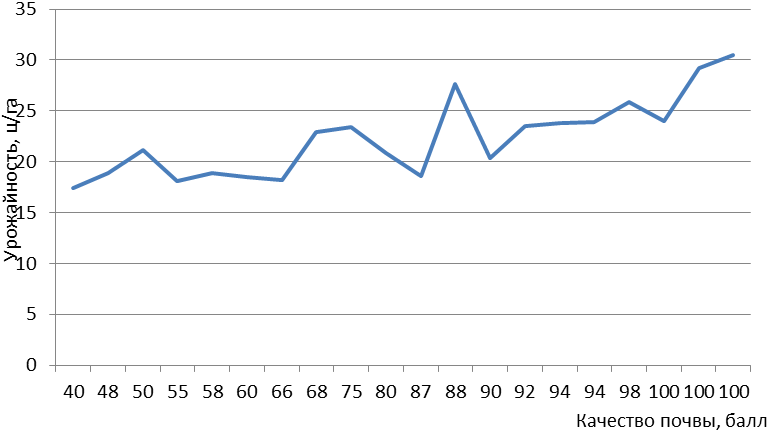
Рис. 29. Зависимость урожайности от качества почвы

а) рассмотрим линейную функцию, выраженную уравнением прямой линии:

(63)

где - урожайность зерновых, ц/га;

- качество почвы, бал.;

- параметры уравнения связи, которые следует определить на основе решения системы нормальных уравнений с двумя неизвестными:

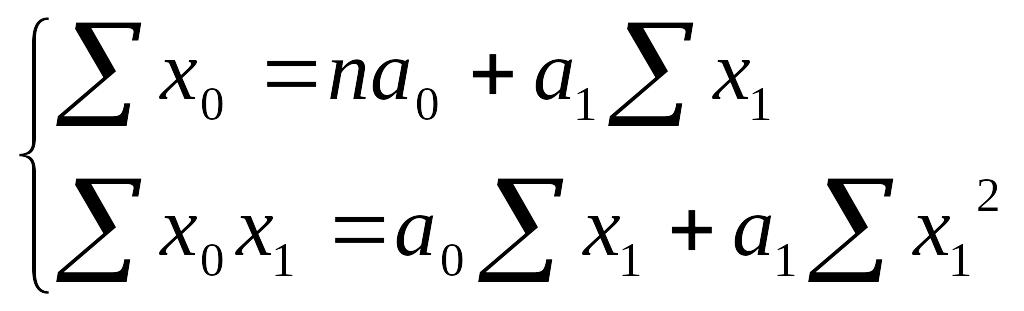(64)

Для удобства расчетов заполним таблицу 259.

Таблица 259 - Данные для уравнения связи и коэффициента корреляции

№ хозяйства	Урожайность зерновых, ц/га	Качество почвы, балл	Расчетные данные			Ожидаемое значение урожайности в зависимости от качества почвы
1	17,3	40	299,29	1600	692	17,7944	-0,2737	1,582081
2	17,9	42	320,41	1764	751,8	18,0862	-0,2191	1,224022
3	21,2	45	449,44	2025	954	18,5239	2,5355	11,95991
4	20,5	48	420,25	2304	984	18,9616	1,2901	6,293171
5	21,2	48	449,44	2304	1017,6	18,9616	1,4447	6,814623
6	18,6	61	345,96	3721	1134,6	20,8583	-1,7007	9,143548
7	19,5	65	380,25	4225	1267,5	21,4419	-1,3461	6,903077
8	19,8	66	392,04	4356	1306,8	21,5878	-1,5915	8,037879
9	24	74	576	5476	1776	22,755	2,0631	8,59625
10	21,2	75	449,44	5625	1590	22,9009	-1,2823	6,048585
11	19,5	79	380,25	6241	1540,5	23,4845	-3,5277	18,09077
12	28	84	784	7056	2352	24,214	4,4269	15,81036
13	22,5	85	506,25	7225	1912,5	24,3599	-1,6185	7,193333
14	24	86	576	7396	2064	24,5058	-0,6639	2,76625
15	24,5	87	600,25	7569	2131,5	24,6517	-0,7093	2,895102
16	22,5	95	506,25	9025	2137,5	25,8189	-3,2547	14,46533
17	24,3	100	590,49	10000	2430	26,5484	-2,0001	8,230864
18	30,5	100	930,25	10000	3050	26,5484	3,6545	11,98197
19	28,5	100	812,25	10000	2850	26,5484	1,1091	3,891579
20	29,6	100	876,16	10000	2960	26,5484	1,6637	5,620608
Итого	455,1	1480	10644,67	117912	34902,3	455,1	2,1316E-14	157,5493

Данные таблицы 259 занесем в систему уравнения.

Разделив оба уравнения на коэффициент при , т.е. первое на 20, второе - на 1543, получим:

Вычтем из большего уравнения меньшее, в данном случае из второго первое:

.

Решим задачу методом определителей: определитель системы равен:

Уравнение регрессии составит:

Используя статистическую функцию ЛИНЕЙН в MS Excel (Windows 7) получим следующее решение (рис. 30).

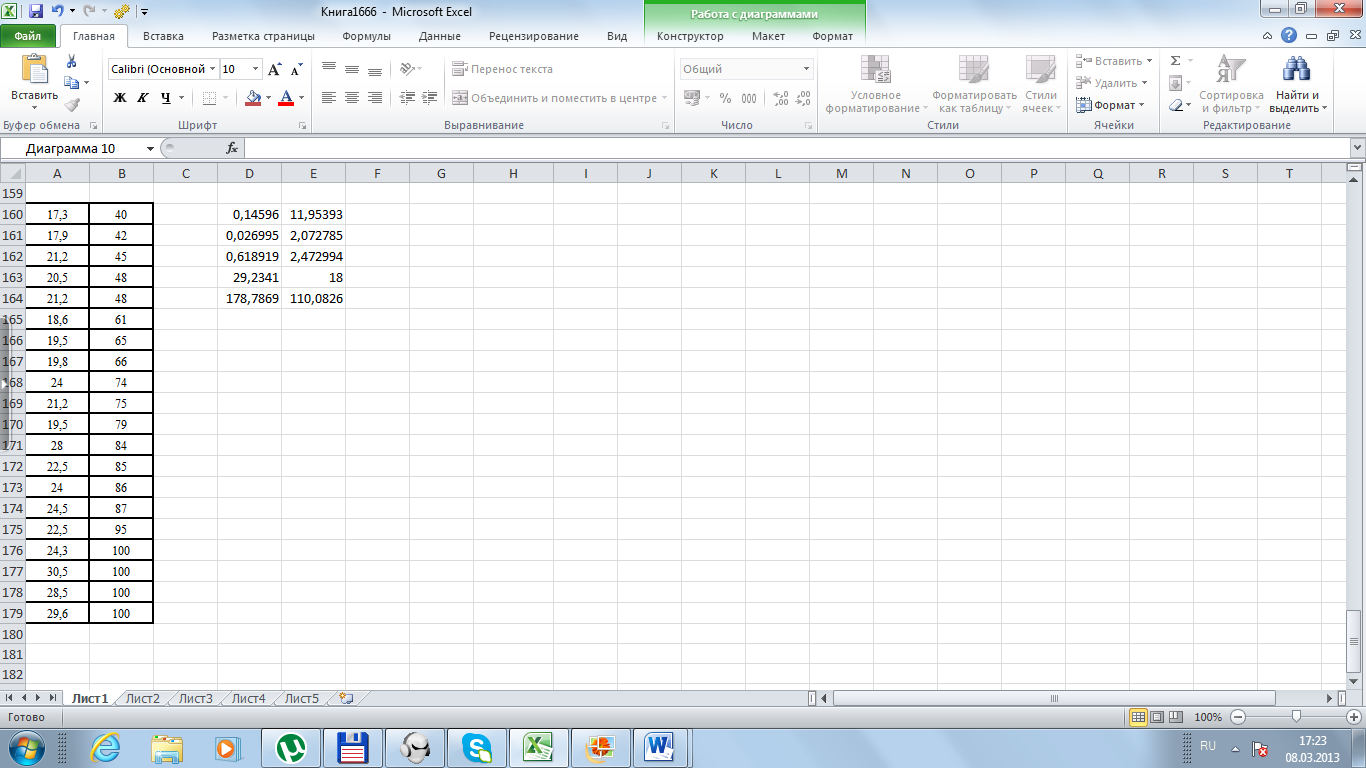
Рис. 30. Регрессионная статистика функции ЛИНЕЙН

Мы получили следующую функцию Коэффициент детерминации составил 0,62.

Коэффициент регрессии (параметр ), равный 0,1459, показывает, что с увеличением балла почвы на единицу урожайность в данных конкретных условиях возрастает на 0,1459 ц/га.

Определим тесноту связи между изучаемыми признаками, для чего рассчитаем коэффициент корреляции по формулам:

. (65)

(66)

Для определения коэффициента корреляции надо определить средние значения , , а также средние квадратические отклонения по результативному и факторному признакам. Все исходные и расчетные данные имеются в таблице 259.

,

, ,

Коэффициент парной линейной корреляции можно рассчитать и по другой формуле, если известен коэффициент регрессии:

Рассчитанный коэффициент корреляции показал существенную зависимость урожайности зерновых от качества почв. Коэффициент детерминации показывает, что на 25 % урожайность в данных условиях зависит от качества почвы, а на 75 % - от других факторов, которые не рассматривались в задаче.

Рассчитаем F-критерий Фишера по формуле:

Если возьмем коэффициент детерминации по данным рис. 30, то получим следующий F-критерий Фишера:

Этот расчет совпадает с рис. 30.

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

Решим эту задачи с помощью программы Statgraphics:

1. Откроем таблицу данных и введем значения;

2. В главном меню выберем Ralate/ Simple Regression;

3. Заполним поля у и х, нажмем на OK три раза (рис. 31…33) и получаем результат (рис. 34).

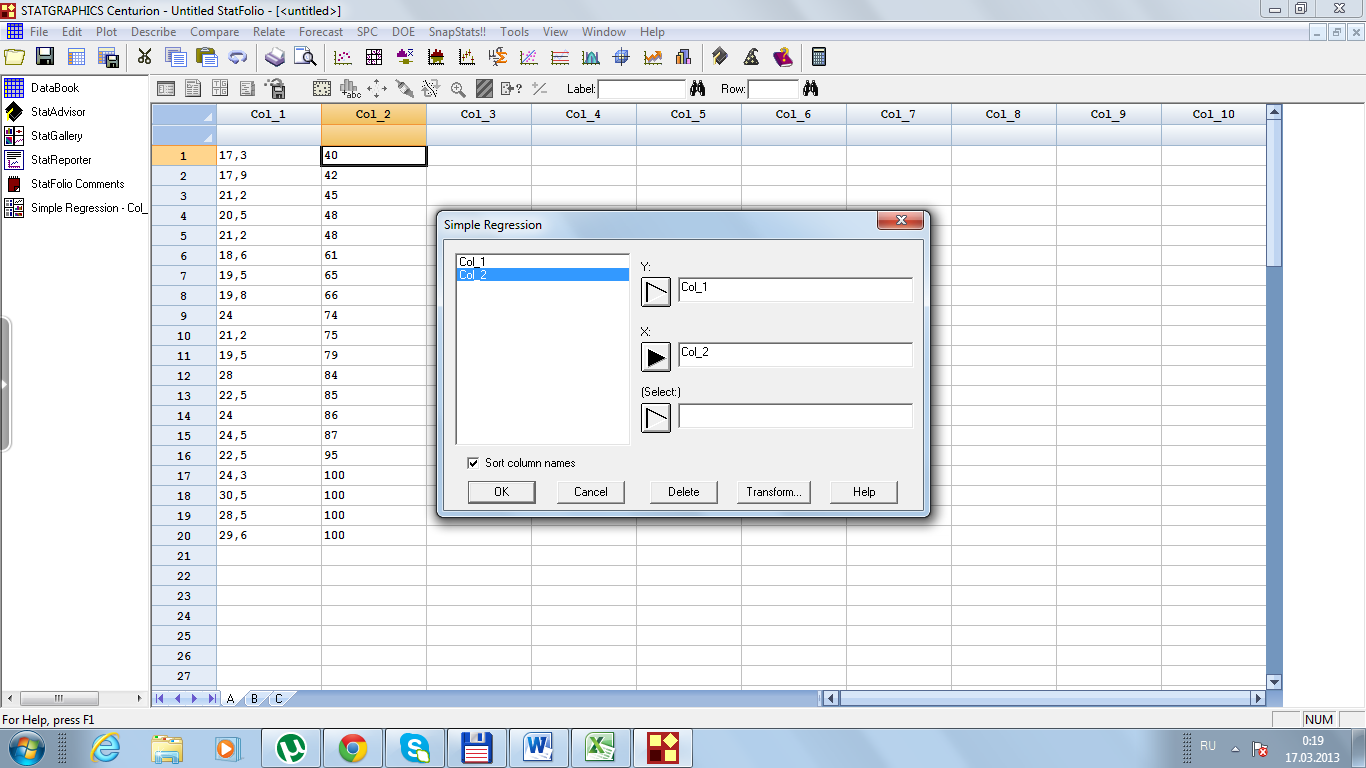
Рис. 31. Диалоговое окно Simple Regression

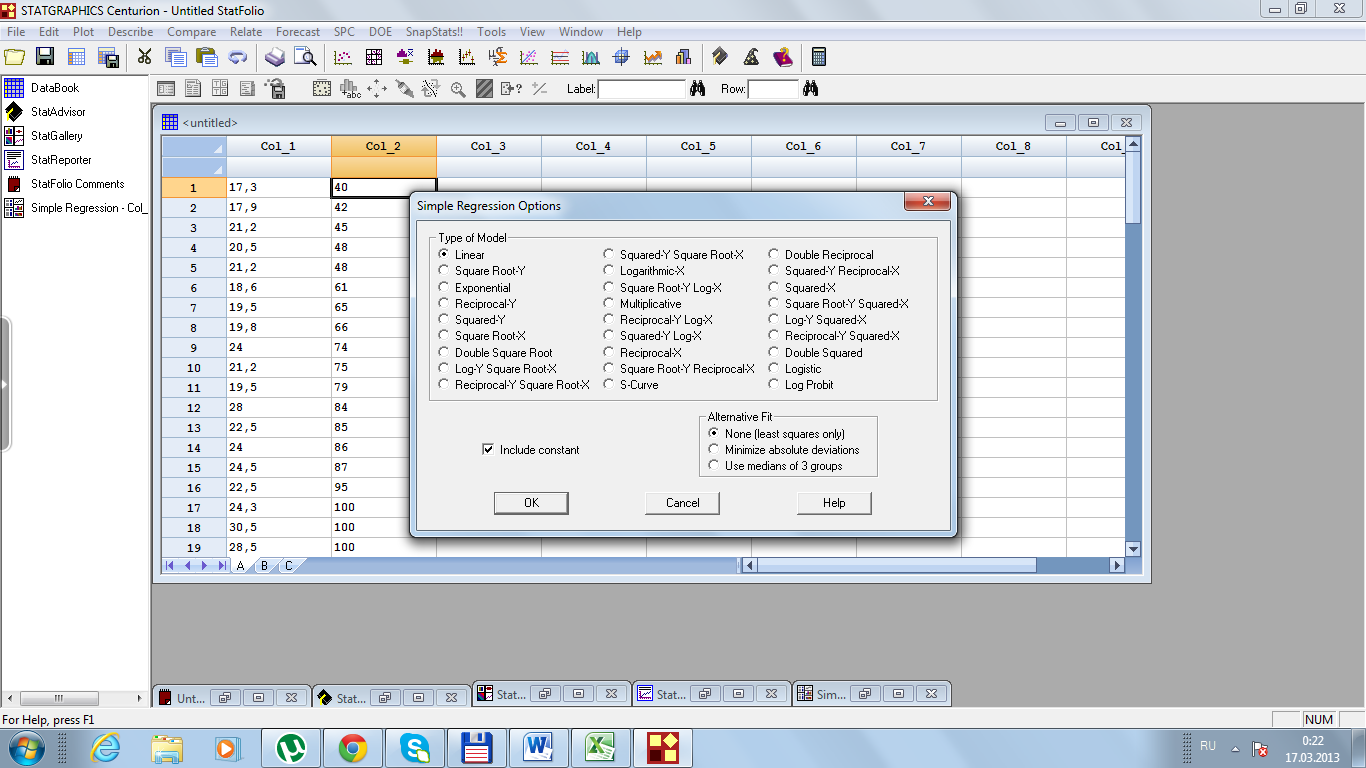
Рис. 32. Диалоговое окно Simple Regression Options

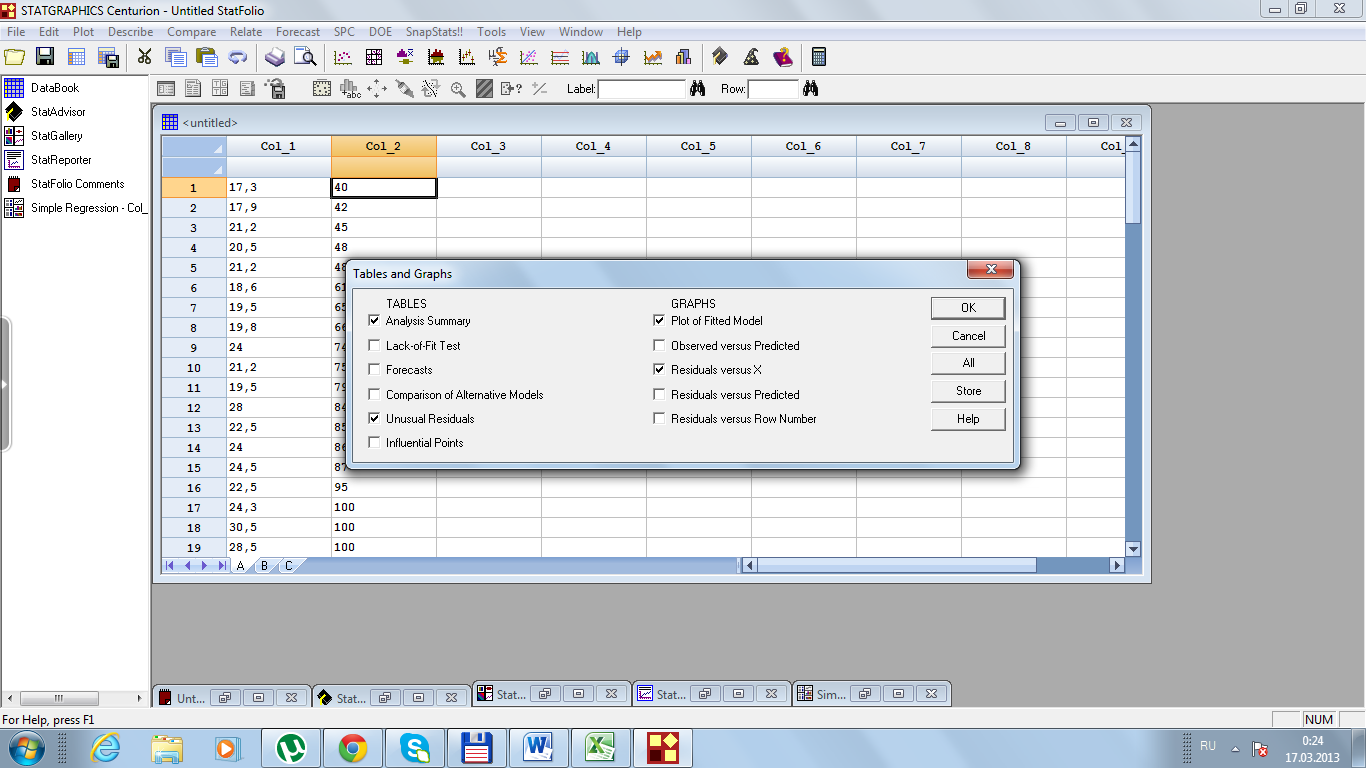
Рис. 33. Диалоговое окно Tables and Graphs

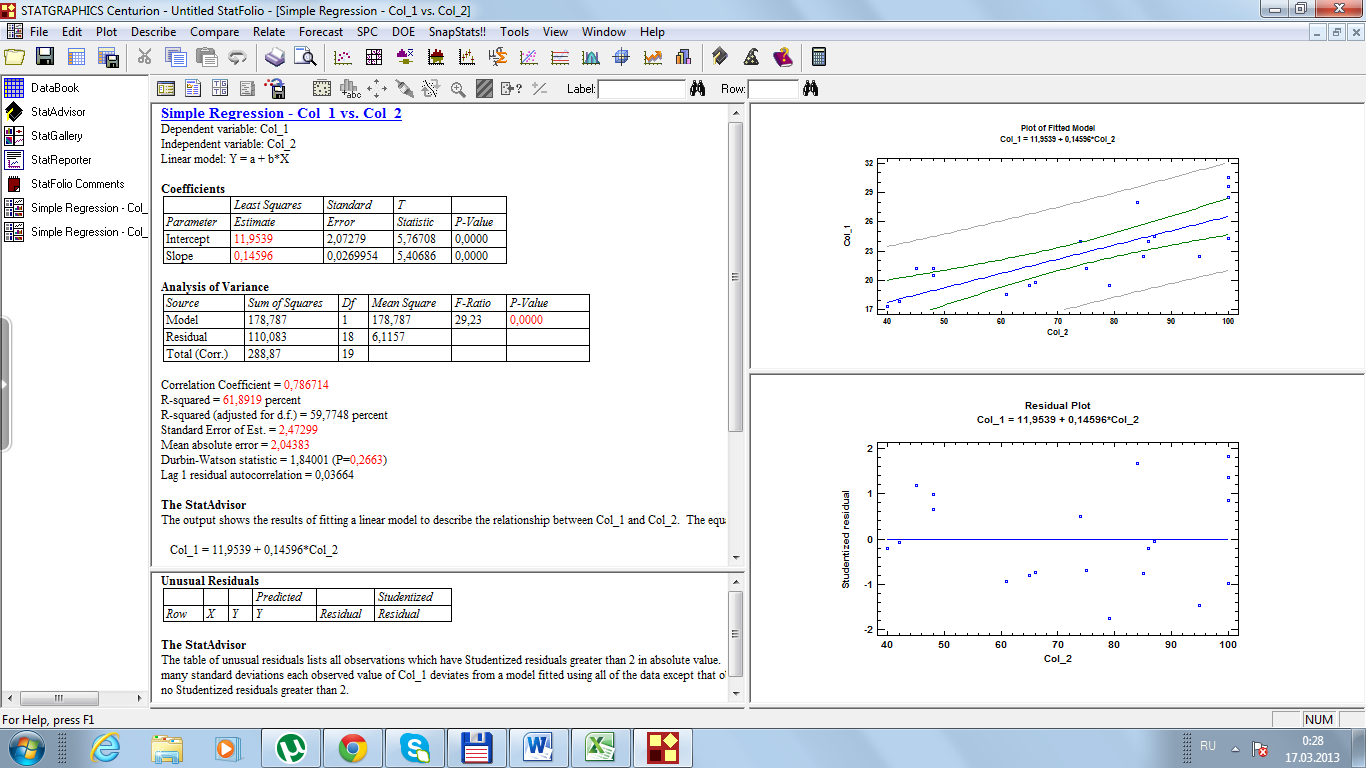
Рис. 34. Результаты расчетов

Определим эмпирическое корреляционное отношение по формуле:

или 78,68.

Определим теоретическое корреляционное отношение по формуле:

Таким образом, мы получили те же значения и уравнение регрессии составило: Из рисунка 34 видно, что случайные ошибки параметров и равны и . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: и . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости , т.е. с вероятностью 0,95 составит 2,1098, , т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.

Чуть ниже на рис. 34 представлен расчет F-критерий Фишера, и он составляет 29,23. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

Отсюда же берем нескорректированный коэффициент детерминации , который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.

Помощью инструмента анализа данных Регрессия получим следующие данные (рис. 35).

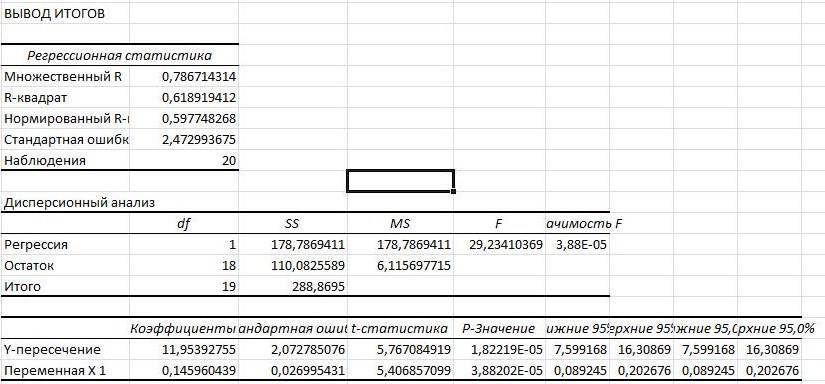
Рис. 35. Регрессионная статистика

Как видим из рис. 35 уравнение регрессии полностью совпадает.

б) рассмотрим степенную функцию:

(67)

Линеаризуем модель логарифмированием:

Пусть , ,

Тогда получим линейное уравнение: .

Для удобства расчетов заполним таблицу 260.

Таблица 260 - Данные для уравнения связи и индекса корреляции

№ хозяйства
1	2,850707	3,688879	10,51591	8,126528	13,60783	2,879097	17,7982	0,248206	29,75703
2	2,884801	3,73767	10,78243	8,322075	13,97017	2,898926	18,15464	0,064843	23,57103
3	3,054001	3,806662	11,62555	9,326923	14,49068	2,926966	18,67089	6,39639	2,418025
4	3,020425	3,871201	11,69267	9,122966	14,9862	2,953195	19,16709	1,776646	5,085025
5	3,054001	3,871201	11,82265	9,326923	14,9862	2,953195	19,16709	4,132719	2,418025
6	2,923162	4,110874	12,01675	8,544874	16,89928	3,0506	21,12802	6,390899	17,26403
7	2,970414	4,174387	12,39966	8,823362	17,42551	3,076413	21,68049	4,754532	10,59503
8	2,985682	4,189655	12,50898	8,914297	17,55321	3,082618	21,81543	4,061964	8,732025
9	3,178054	4,304065	13,67855	10,10003	18,52498	3,129115	22,85375	1,313896	1,550025
10	3,054001	4,317488	13,18561	9,326923	18,6407	3,13457	22,97876	3,16399	2,418025
11	2,970414	4,369448	12,97907	8,823362	19,09207	3,155687	23,46916	15,75425	10,59503
12	3,332205	4,430817	14,76439	11,10359	19,63214	3,180628	24,06187	15,5089	27,51003
13	3,113515	4,442651	13,83226	9,693978	19,73715	3,185438	24,17787	2,81526	0,065025
14	3,178054	4,454347	14,15616	10,10003	19,84121	3,190191	24,29307	0,085892	1,550025
15	3,198673	4,465908	14,28498	10,23151	19,94434	3,19489	24,40748	0,00856	3,045025
16	3,113515	4,553877	14,17857	9,693978	20,73779	3,230641	25,29587	7,816884	0,065025
17	3,190476	4,60517	14,69269	10,17914	21,20759	3,251487	25,82872	2,336998	2,387025
18	3,417727	4,60517	15,73921	11,68086	21,20759	3,251487	25,82872	21,82082	59,98503
19	3,349904	4,60517	15,42688	11,22186	21,20759	3,251487	25,82872	7,135714	33,00503
20	3,387774	4,60517	15,60128	11,47702	21,20759	3,251487	25,82872	14,22252	46,85403
Итого	62,22751	85,20981	265,8842	194,1402	364,8998	62,22812	452,4346	119,8099	288,8695
В среднем	3,111375	4,260491	13,29421	9,70701	18,24499	2,879097	17,7982		29,75703

Получим систему нормальных уравнений:

Коэффициент эластичности 0,4064 показывает, что с ростом качества почвы на 1 балл, урожайность зерновых возрастает на 0,41 ц/га.

Если решить эту систему через статистическую функцию ЛИНЕЙН в MS Excel получим следующее уравнение

Решим эту задачу с помощью программы Statgraphics (рис. 36).

Рис. 36. Результаты расчетов

Получаем уравнение регрессии Из рисунка 36 видно, что случайные ошибки параметров и равны и . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: и . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости , т.е. с вероятностью 0,95 составит 2,1098, , т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,5852, таким образом, на 58,52% вариации объясняется вариацией , на долю прочих факторов приходится 23,5 %.

Рассчитаем F-критерий Фишера по формуле:

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Чуть ниже (рис. 36) представлен расчет F-критерий Фишера, и он составляет 26,43. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0001, что не превышает допустимый уровень значимости 5%.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

в) рассмотрим функцию экспоненты:

(68)

Для оценки параметров приведем уравнение к линейному виду:

Воспользуемся методом наименьших квадратов и получим систему уравнений:

Для удобства расчетов заполним таблицу 261.

Таблица 261 - Данные для уравнения связи и индекса корреляции

№ хозяйства
1	0,0578	40	2,3121	1600	114,0283	18,0970	0,6352	29,757	0,0461
2	0,0559	42	2,3464	1764	121,1616	18,3279	0,1831	23,571	0,0239
3	0,0472	45	2,1226	2025	137,4301	18,67984	6,3512	2,4180	0,1189
4	0,0488	48	2,3415	2304	144,9804	19,03853	2,1360	5,0850	0,0713
5	0,0472	48	2,2642	2304	146,5921	19,03853	4,6720	2,4180	0,1020
6	0,0538	61	3,2796	3721	178,3129	20,67416	4,302147	17,2640	0,1115
7	0,0513	65	3,3333	4225	193,0769	21,20516	2,90762	10,5950	0,0874
8	0,0505	66	3,3333	4356	197,055	21,34003	2,3717	8,7320	0,0778
9	0,0417	74	3,0833	5476	235,176	22,45032	2,4015	1,5500	0,0646
10	0,0472	75	3,5378	5625	229,0501	22,5931	1,9407	2,4180	0,0657
11	0,0513	79	4,0513	6241	234,6627	23,1734	13,4938	10,5950	0,1884
12	0,0357	84	3	7056	279,9052	23,9198	16,6484	27,5100	0,1457
13	0,0444	85	3,7778	7225	264,6488	24,0719	2,4708	0,0650	0,0699
14	0,0417	86	3,5833	7396	273,3126	24,2250	0,0506	1,5500	0,0094
15	0,0408	87	3,5510	7569	278,2846	24,3791	0,0146	3,0450	0,0049
16	0,0444	95	4,2222	9025	295,784	25,6475	9,9065	0,0650	0,1399
17	0,0413	100	4,1152	10000	319,0476	26,4735	4,7242	2,3870	0,0894
18	0,0328	100	3,2787	10000	341,7727	26,4735	16,2126	59,9850	0,1320
19	0,0351	100	3,5088	10000	334,9904	26,4735	4,1067	33,0050	0,0711
20	0,0338	100	3,3784	10000	338,7774	26,4735	9,7749	46,8540	0,1056
Итого	0,9024	1480	64,4208	117912	4658,049	452,7551	105,3042	288,8695	1,7255

Получим систему нормальных уравнений:

Сделаем потенцирование

.

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,6365, таким образом, на 63,65 % вариации объясняется вариацией , на долю прочих факторов приходится 36,47 %.

Рассчитаем F-критерий Фишера по формуле:

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

Решим эту задачу с помощью программы Statgraphics (рис. 37).

Таким образом, мы получили те же значения и уравнение регрессии . Из рисунка 37 видно, что случайные ошибки параметров и равны и . На их основе рассчитываются значения t-критерия Стьюдента: и . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости , т.е. с вероятностью 0,95 составит 2,1098, , т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.

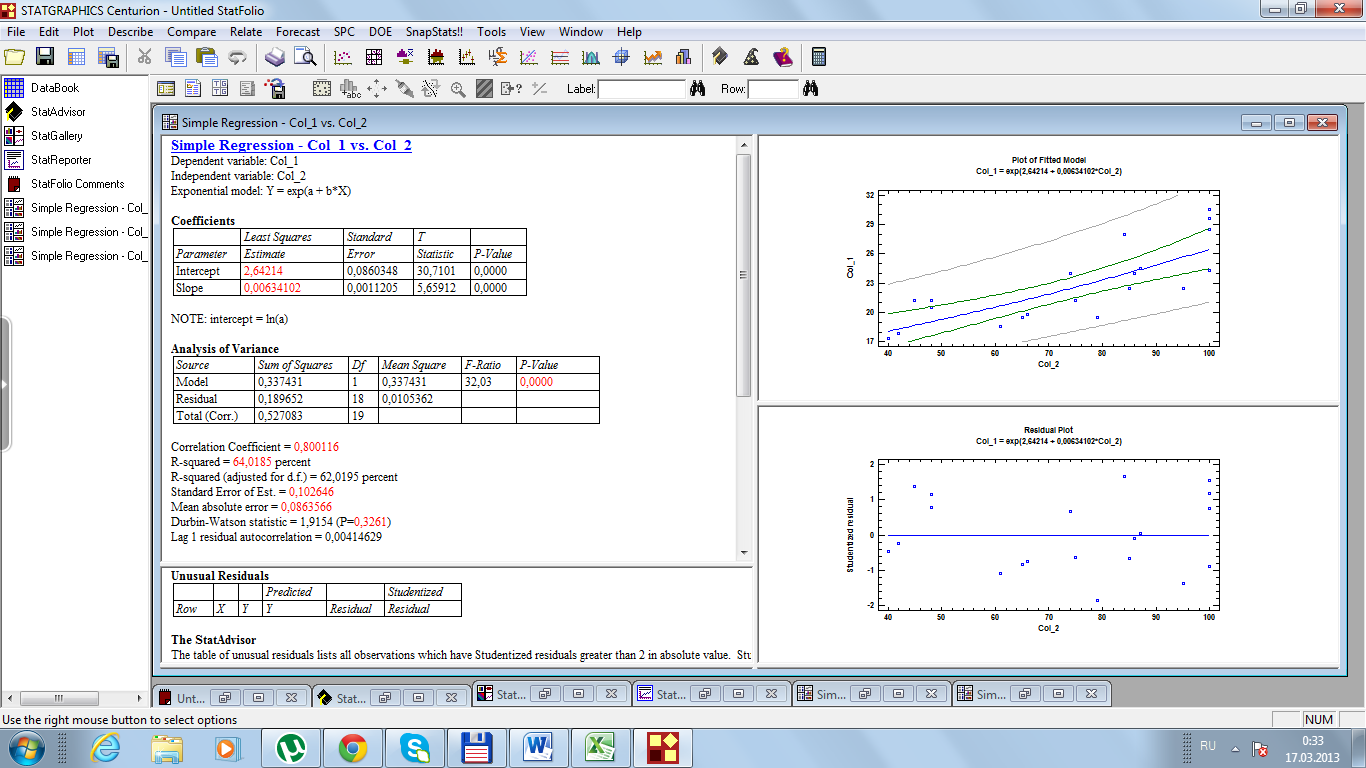
Рис. 37. Результаты расчетов

Чуть ниже на рис. 37 представлен расчет F-критерий Фишера, и он составляет 32,03. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

г) рассмотрим функцию показательной кривой:

(69)

Для оценки параметров приведем уравнение к линейному виду:

Воспользуемся методом наименьших квадратов и получим систему уравнений:

Получим систему нормальных уравнений:

Получаем уравнение регрессии:

Сделаем потенцирование и получим

; ; , , получаем

.

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,6282, таким образом, на 62,82% вариации объясняется вариацией , на долю прочих факторов приходится 37,18 %.

Рассчитаем F-критерий Фишера по формуле:

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

Эту задачу решим с помощью статистической функции ЛГРФПРИБЛ (рис. 38).

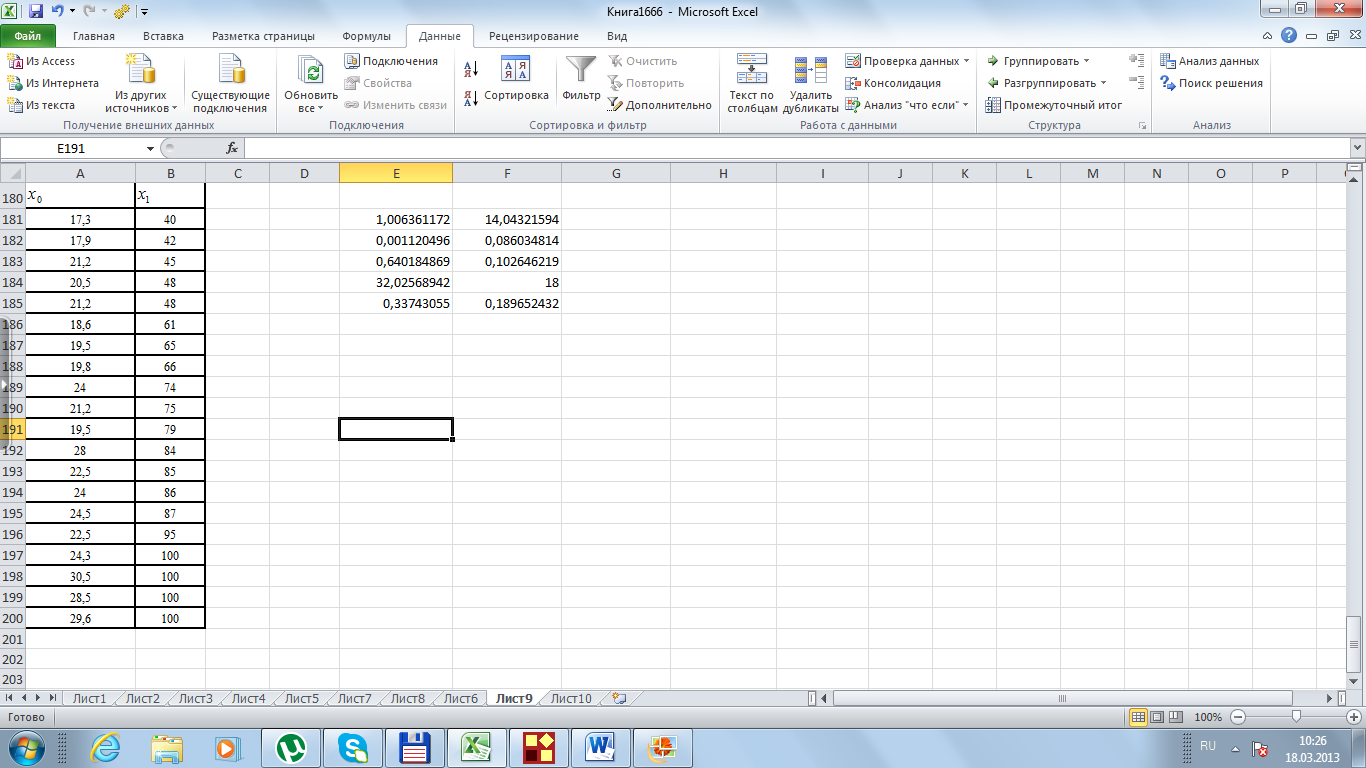
Рис. 38. Решение статистической функции ЛГРФПРИБЛ

Таким образом, мы получаем уравнение регрессии .

д) рассмотрим функцию равносторонней гиперболы:

. (70)

Для оценки параметров приведем уравнение к линейному виду при . Затем получим

Воспользуемся методом наименьших квадратов и получим систему уравнений:

Таблица 262 - Данные для уравнения связи и коэффициента корреляции

№ хозяйства
1	17,3	0,025	0,4325	0,000625	17,39276	0,00860349	-0,53616
2	17,9	0,0238095	0,42619	0,000567	18,0186	0,01406483	-0,66254
3	21,2	0,0222222	0,47111	0,000494	18,85305	5,508179518	11,07052
4	20,5	0,0208333	0,42708	0,000434	19,5832	0,84052988	4,472215
5	21,2	0,0208333	0,44167	0,000434	19,5832	2,614055713	7,626435
6	18,6	0,0163934	0,30492	0,000269	21,91727	11,00429439	-17,8348
7	19,5	0,0153846	0,3	0,000237	22,44762	8,688454595	-15,116
8	19,8	0,0151515	0,3	0,00023	22,57016	7,673789783	-13,9907
9	24	0,0135135	0,32432	0,000183	23,43127	0,32345658	2,369718
10	21,2	0,0133333	0,28267	0,000178	23,52599	5,410226379	-10,9716
11	19,5	0,0126582	0,24684	0,00016	23,8809	19,19225154	-22,4661
12	28	0,0119048	0,33333	0,000142	24,277	13,86074673	13,29644
13	22,5	0,0117647	0,26471	0,000138	24,35063	3,424816156	-8,225
14	24	0,0116279	0,27907	0,000135	24,42254	0,178541624	-1,76059
15	24,5	0,0114943	0,28161	0,000132	24,4928	5,17738E-05	0,029369
16	22,5	0,0105263	0,23684	0,000111	25,00165	6,258276422	-11,1185
17	24,3	0,01	0,243	0,0001	25,27834	0,957153069	-4,0261
18	30,5	0,01	0,305	0,0001	25,27834	27,26571227	17,12019
19	28,5	0,01	0,285	0,0001	25,27834	10,37908027	11,30406
20	29,6	0,01	0,296	0,0001	25,27834	18,67672787	14,6002
Итого	455,1	0,296451	6,48186	0,004868	454,862	142,2790129	-24,819

Получим систему нормальных уравнений:

Получаем уравнение регрессии:

Решим эту задачу с помощью программы Statgraphics (рис. 39).

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,5075, таким образом, на 50,75% вариации объясняется вариацией , на долю прочих факторов приходится 49,25 %.

Рассчитаем F-критерий Фишера по формуле:

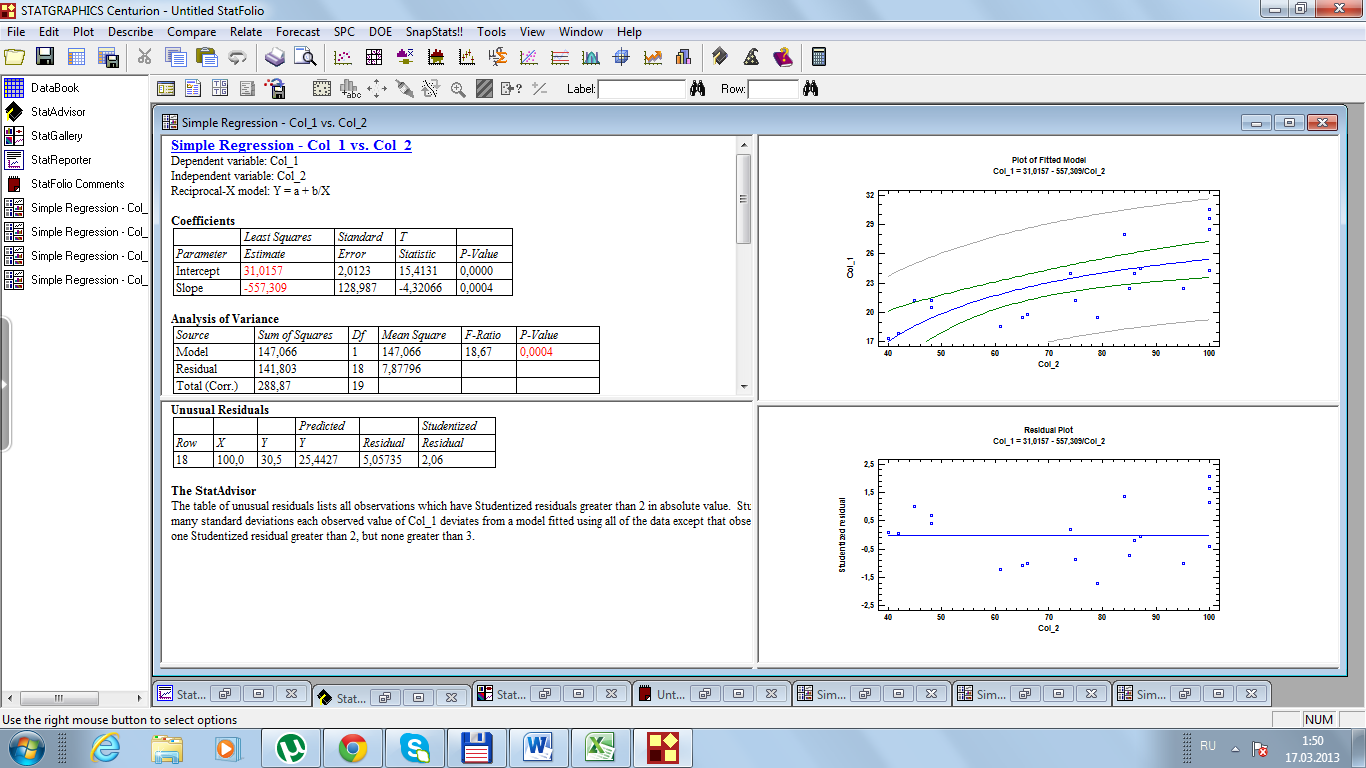
Рис. 39. Результаты расчетов

Таким образом, мы получили те же значения. Небольшие различия объясняются округлением.

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

е) рассмотрим обратную функцию:

. (71)

Для оценки параметров приведем уравнение к линейному виду при . Затем получим

Воспользуемся методом наименьших квадратов и получим систему уравнений:

Таблица 263 - Данные для уравнения связи и коэффициента корреляции

№ хозяйства
1	0,0578035	40	2,3121387	1600	19,2678227	3,8723263	11,3747
2	0,0558659	42	2,3463687	1764	19,4174757	2,3027326	8,477518
3	0,0471698	45	2,1226415	2025	19,6463654	2,4137804	7,328465
4	0,0487805	48	2,3414634	2304	19,8807157	0,383513	3,020899
5	0,0471698	48	2,2641509	2304	19,8807157	1,740511	6,223039
6	0,0537634	61	3,2795699	3721	20,9643606	5,590201	12,71162
7	0,0512821	65	3,3333333	4225	21,3219616	3,3195441	9,343393
8	0,0505051	66	3,3333333	4356	21,4132762	2,6026602	8,14786
9	0,0416667	74	3,0833333	5476	22,172949	3,3381153	7,612712
10	0,0471698	75	3,5377358	5625	22,2717149	1,1485729	5,055259
11	0,0512821	79	4,0512821	6241	22,675737	10,085305	16,28583
12	0,0357143	84	3	7056	23,2018561	23,022184	17,13623
13	0,0444444	85	3,7777778	7225	23,3100233	0,6561378	3,600104
14	0,0416667	86	3,5833333	7396	23,4192037	0,3373243	2,419984
15	0,0408163	87	3,5510204	7569	23,5294118	0,9420415	3,961585
16	0,0444444	95	4,2222222	9025	24,4498778	3,8020232	8,666123
17	0,0411523	100	4,1152263	10000	25,0626566	0,5816452	3,138505
18	0,0327869	100	3,2786885	10000	25,0626566	29,564703	17,82736
19	0,0350877	100	3,5087719	10000	25,0626566	11,815329	12,06085
20	0,0337838	100	3,3783784	10000	25,0626566	20,587485	15,32886
Итого	0,9023554	1480	64,42077	117912	447,074094	128,10614	179,7209

Получим систему нормальных уравнений:

Получаем уравнение регрессии:

Решим эту задачу с помощью программы Statgraphics (рис. 40).

Таким образом, мы получили те же значения. Небольшие различия объясняются округлением.

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,5565, таким образом, на 55,65% вариации объясняется вариацией , на долю прочих факторов приходится 44,35 %.

Рассчитаем F-критерий Фишера по формуле:

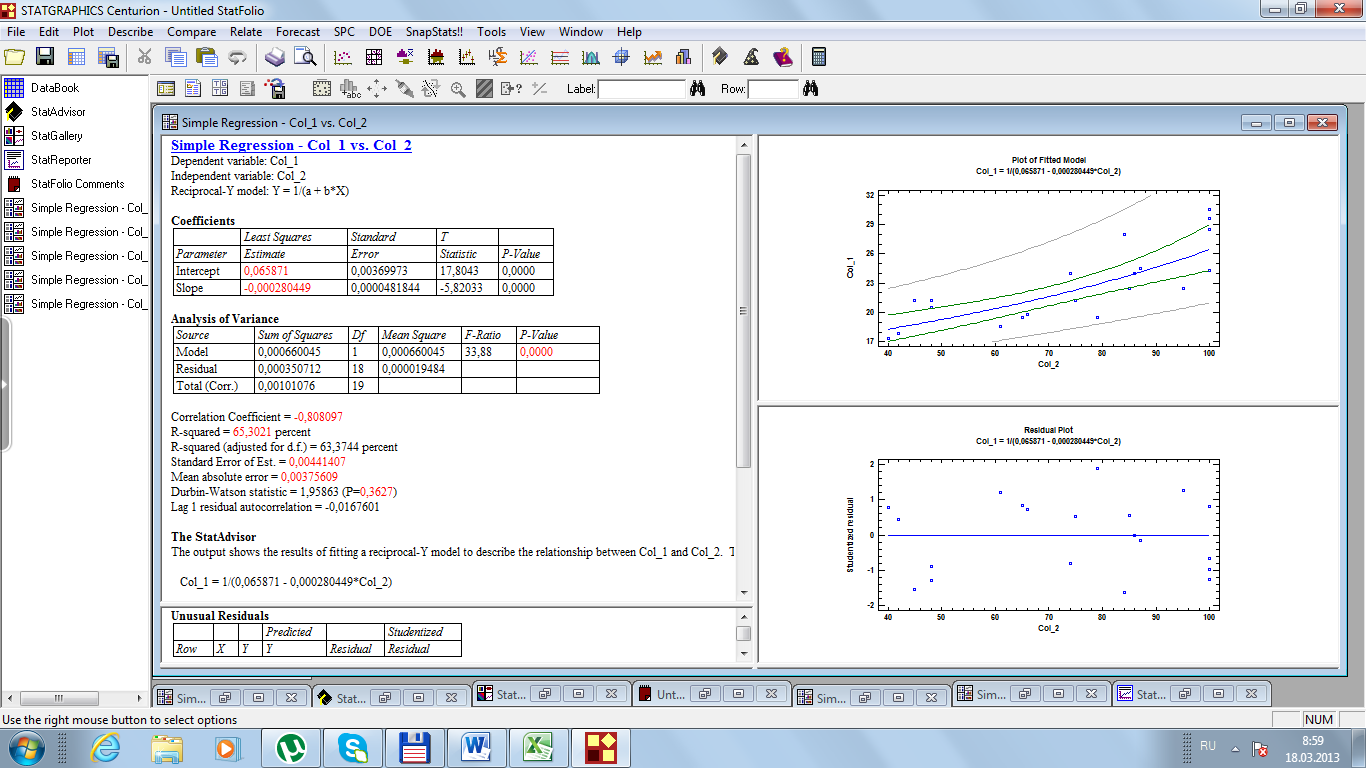
Рис. 40. Результаты расчетов

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

ж) рассмотрим функцию:

. (72)

Воспользуемся программой Statgraphics (рис. 41) и получим уравнение регрессии: .

Таблица 264 - Данные для расчета коэффициентов

№ хозяйства
1	2	3	4	5	6
1	17,3	40	17,309697	9,40261E-05	0,056050315
2	17,9	42	17,70052	0,039792138	1,114411557
3	21,2	45	18,271088	8,578526578	13,81562351
4	20,5	48	18,824369	2,807738202	8,173808233
5	21,2	48	18,824369	5,643621165	11,20580513
6	18,6	61	21,054577	6,02494794	13,1966502
7	19,5	65	21,694719	4,81679326	11,2549713
8	19,8	66	21,851825	4,209986222	10,36275301
9	24	74	23,070187	0,86455174	3,874219769
10	21,2	75	23,217988	4,072274111	9,518809617
11	19,5	79	23,800012	18,4901066	22,05134562
12	28	84	24,508114	12,19326952	12,47102229
13	22,5	85	24,647293	4,610867034	9,543524244

Продолжение таблицы 264

1	2	3	4	5	6
14	24	86	24,785691	0,617309766	3,273710958
15	24,5	87	24,92332	0,179199656	1,72783593
16	22,5	95	25,998137	12,2369655	15,54727748
17	24,3	100	26,647893	5,512601421	9,662111008
18	30,5	100	26,647893	14,83872853	12,6298591
19	28,5	100	26,647893	3,430300433	6,498621141
20	29,6	100	26,647893	8,714935888	9,973334544
Итого	455,1	1480	457,07348	117,8826097	185,9517449

Решим эту задачу с помощью программы Statgraphics (рис. 41):

Рис. 41. Результаты расчетов

Тесноту связи определим, рассчитав индекс корреляции:

Коэффициент детерминации составил 0,5919, таким образом, на 59,19% вариации объясняется вариацией , на долю прочих факторов приходится 40,81 %.

Рассчитаем F-критерий Фишера по формуле:

Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Определим среднюю ошибку апроксимации по формуле:

Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных и фактических данных не столь велико.

Теперь необходимо определить наиболее точную модель, учитывая коэффициенты детерминации и апроксимации. Так, уравнение регрессии наиболее точно отражает исходные данные. Так как коэффициент детерминации наибольший, а коэффициент апроксимации наименьший.

Задача 2. Имеются данные об урожайности картофеля, количество внесенных удобрений и доле высокосортных посевов (табл. 265). Определите показатели связи при множественной линейной зависимости расчетным путем с помощью инструмента анализа данных Регрессия и программы Statgraphics.

Таблица 265 - Данные для уравнения связи и коэффициента множественной корреляции

Номер хозяйства	Исходные данные			Расчетные данные
	урожайность картофеля, ц/га ( )	внесено органических удобрений, т/га ( )	удельный вес высокосортных посевов, %
1	2	3	4	5	6	7	8	9	10
1	120	13	60	14400	169	3600	1560	7200	780
2	130	15	60	16900	225	3600	1950	7800	900
3	250	28	100	62500	784	10000	7000	25000	2800
4	200	25	95	40000	625	9025	5000	19000	2375
5	130	14	66	16900	196	4356	1820	8580	924
6	100	10	50	10000	100	2500	1000	5000	500
7	110	12	56	12100	144	3136	1320	6160	672
8	180	19	78	32400	361	6084	3420	14040	1482
9	120	14	58	14400	196	3364	1680	6960	812
10	160	15	70	25600	225	4900	2400	11200	1050
11	190	20	90	36100	400	8100	3800	17100	1800
12	180	17	81	32400	289	6561	3060	14580	1377
13	170	16	77	28900	256	5929	2720	13090	1232
14	140	17	60	19600	289	3600	2380	8400	1020
15	110	14	55	12100	196	3025	1540	6050	770
16	170	15	78	28900	225	6084	2550	13260	1170
17	210	23	96	44100	529	9216	4830	20160	2208
18	230	27	100	52900	729	10000	6210	23000	2700
19	190	20	90	36100	400	8100	3800	17100	1800
20	200	20	88	40000	400	7744	4000	17600	1760
Итого	3290	354	1508	576300	6738	118924	62040	261280	28132

Исследование формы зависимости между указанными признаками позволяет сделать вывод, что связь может быть выражена при помощи линейного уравнения

(73)

где - урожайность картофеля, ц/га;

- количество внесенных органических удобрений под картофель, т/га;

- удельный вес посевов высокосортными семенами, %.

Требуется определить параметры уравнения связи коэффициент множественной корреляции.

Решение: Составим систему нормальных уравнений с тремя неизвестными:

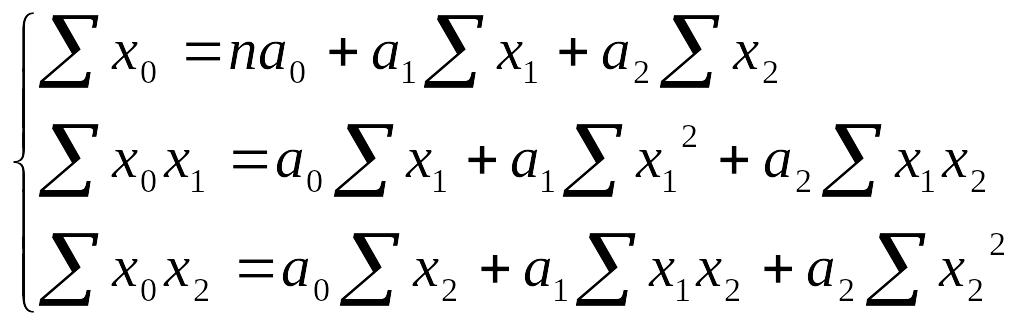(74)

Подставив в эту систему данные из табл. 261, получим:

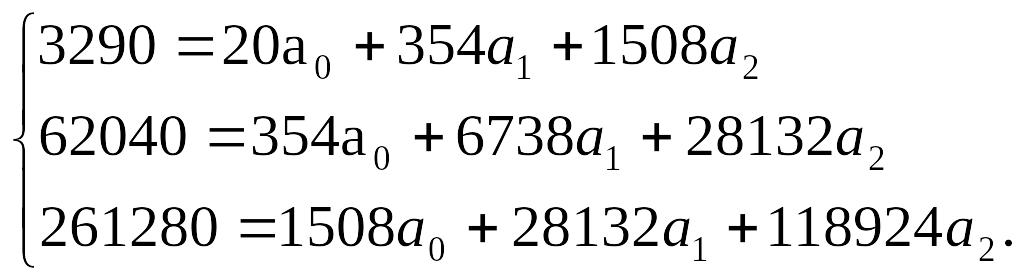
Разделим каждое из уравнений на коэффициенты при первом известном : первое уравнение - на 20, второе - на 354, третье - на 1508, получим:

Теперь поочередно вычтем первое уравнение из второго и третьего:

(175,2 - 164,5) = - + (19,0 - 17,7) + (79,5 - 75,4) ;

(173,3-164,5) = - + (18,6 – 17,7) + (78,9 – 75,4) .

Получим:

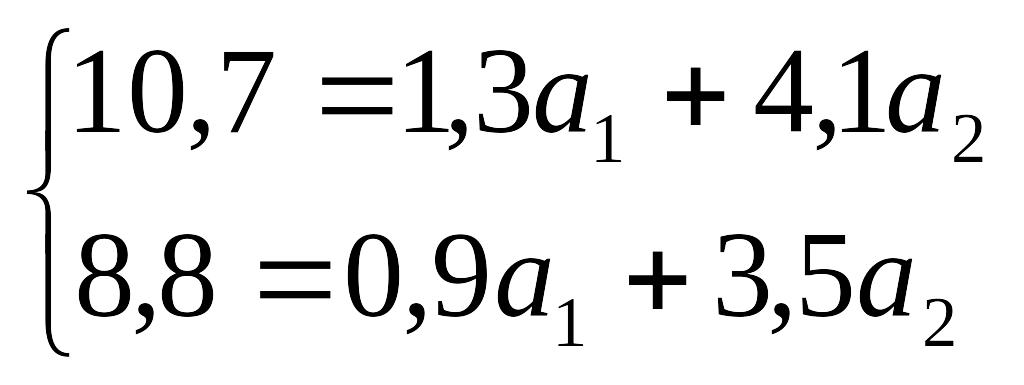
Разделив каждое из двух этих уравнений на коэффициент при , первое уравнение - на 1,3, второе - на 0,9, получим:

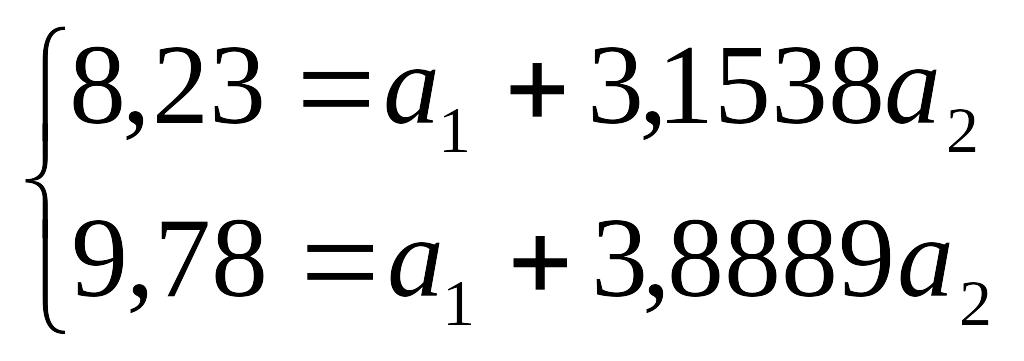
Из второго уравнения вычитаем первое и освобождаемся от параметра : 9,78 -8,23 = (3,8889 - 3,1538)а₂, 1,55 = 0,73 5а₂, отсюда а₂ = 1,55 : 0,735 = 2,11. Подставляем значение а₂ в уравнение 8,23 = + 3,1538 ∙ 2,11, отсюда = 1,58. Далее надо найти значение параметра а_о, для чего используем уравнение 164,5 = + 17,7 ∙ 1,58 + 75,4 ∙ 2,11. Сделаем соответствующие расчеты: 164,5 = + 27,966 + 159,09; отсюда а₀ .= - 22,6. Уравнение множественной линейной зависимости примет вид:

Параметры уравнения множественной регрессии показывают, что с увеличением дозы внесения органических удобрений на 1 т в расчете на 1 га урожайность картофеля возрастает на 1,58 ц, а повышение удельного веса высокосортных семян на 1 % дает прирост урожайности 2,11 ц. Параметр экономического смысла не имеет.

Теперь определим тесноту связи. Рассчитаем множественный (совокупный) коэффициент корреляции по формуле

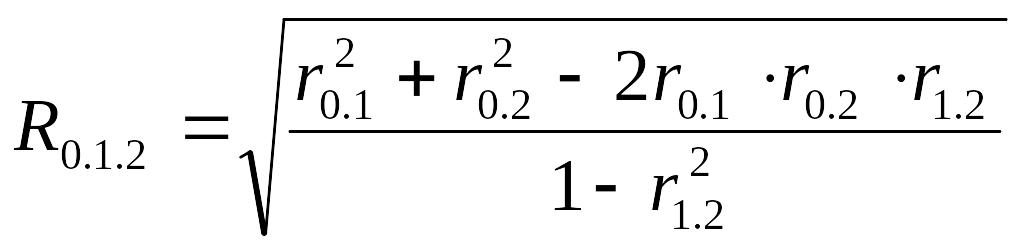(75)

Для его расчета надо найти средние значения , а также средние квадратические отклонения по урожайности, внесению удобрений и удельному весу высокосортных семян:

Теперь рассчитаем средние квадратические отклонения:

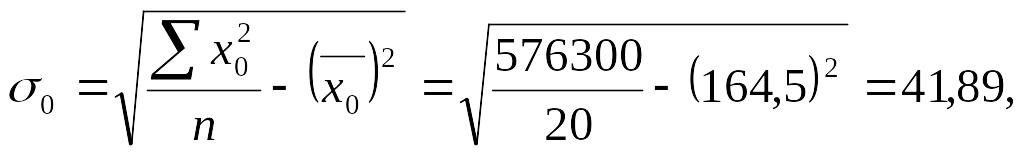
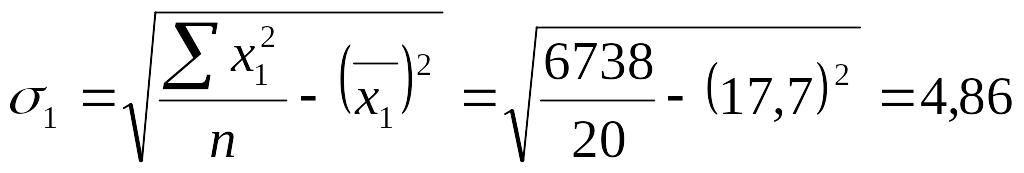
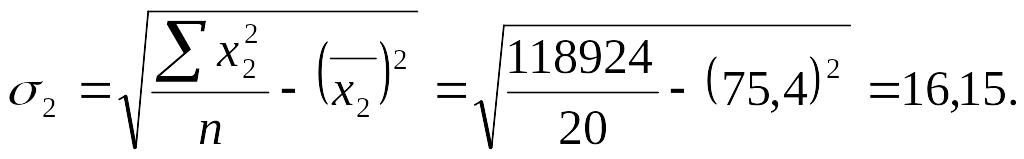
Рассчитаем парные коэффициенты корреляции:

Эти коэффициенты можно рассчитать с помощью MS Excel. В главном меню последовательно выбираем Данные /Анализ данных /Корреляция (рис. 42).

Рис. 42. Расчет коэффициентов корреляции

Так же можно воспользоваться программой Statgraphics, используя в расчетах функцию Multiple Variable Analisis (рис. 43).

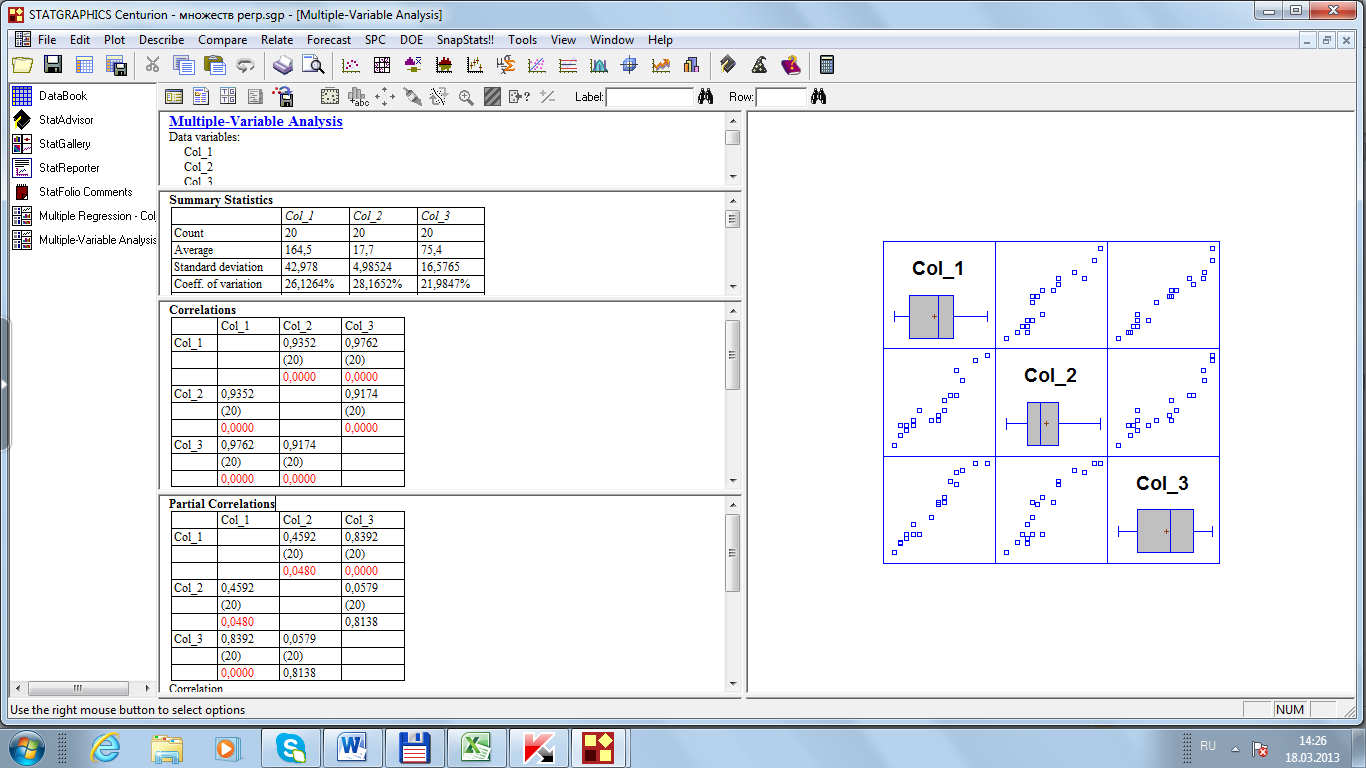
Рис. 43. Расчет коэффициентов корреляции

Подставив значения коэффициента корреляции и детерминации в формулу множественной (совокупной) корреляции получим:

Связь между признаками очень тесная, так как коэффициент множественной корреляции составляет 0,981, а детерминации — 0,962. т.е. 96,2 % колебаний урожайности картофеля в данных условиях зависит от исследуемых факторов и только 3,8 % - от других, не уточненных в анализе.

Значимость оценим t-критерием Стьюдента:

Табличное значение t-критерия Стьюдента при 5 % уровне значимости и 17 степенях свободы (n-m=20-2-1=17) составляет 2,1098. Так как только при условии оба фактора , считаются значимыми. Однако меньше положенного. Поэтому величина является статистически незначимой, ненадежной, т.е. она сформировалась под воздействием случайных факторов. То же касается и величины .

Теперь воспользуемся инструментом анализа данных Регрессия (рис. 43).

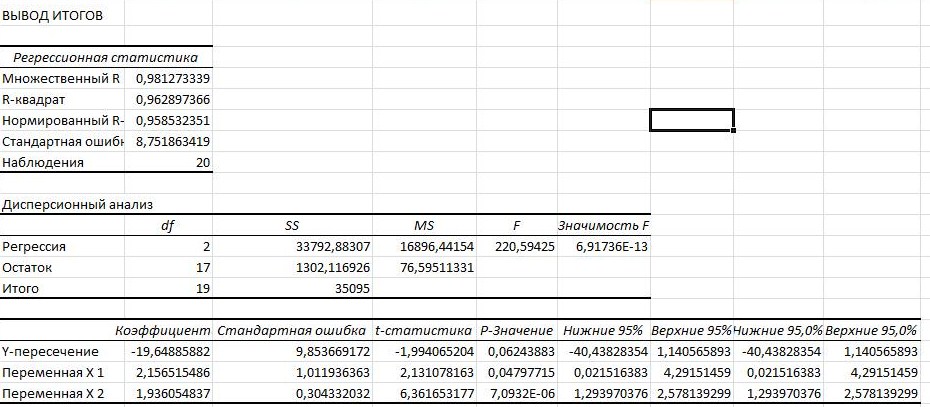
Рис. 43. Результаты расчетов

Уравнение множественной линейной зависимости примет вид: . Коэффициент детерминации 0,9629.

Табличное значение F-критерий Фишера составило 3,59, расчетное – 220,59. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Решим эту же задачу с помощью программы Statgraphics, используя в расчетах функцию Multiple Regression (рис. 44).

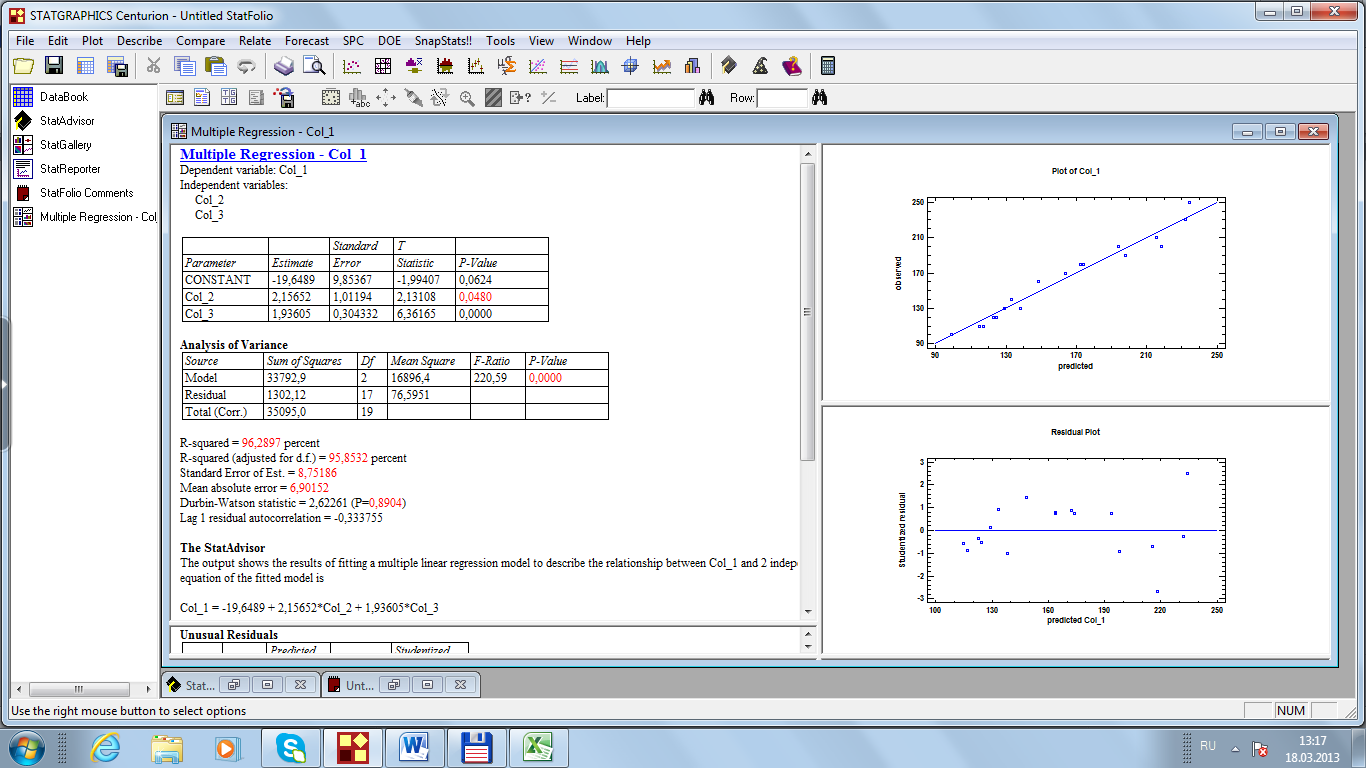
Рис. 44. Результаты расчетов

Уравнение множественной линейной зависимости примет вид: . Случайные ошибки параметров , , равны , , . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: , , . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости , т.е. с вероятностью 0,95 составит 2,1098, , т.е. с вероятностью 0,99 – 2,8982. Статистически значимыми здесь являются , , а величина сформировалась под воздействием случайных причин.

Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так и То есть вероятность случайно получить такие значения t-критерия Стьюдента составляет 4,8 % и 0,0000, что не превышает допустимый уровень значимости 5 %.

Чуть ниже на рис. 44 представлен расчет F-критерий Фишера, и он составляет 29,23. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

Отсюда же берем нескорректированный коэффициент детерминации , который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.

Табличное значение F-критерий Фишера составило 3,59, расчетное – 220,59. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Задание 3. Определение показателей связи при парной криволинейной зависимости.

Имеются данные по группе коров об их продуктивности возрасте (числе отелов) (табл. 266).

Таблица 266 - Данные для уравнения связи и индекса корреляции (корреляционное отношение)

№ п/п	Исходные данные		Расчетные данные
	относительное изменение удоя, %, ( )	возраст коров к моменту отела, лет ( )
1	2	3	4	5	6	7	8	9	10	11
1	79	2	4	8	16	158	316	80,649	198,16	154,45
2	82	2,5	6,25	15,625	39,06	205	512,5	83,965	122,7	83,032
3	87	3	9	27	81	261	783	86,979	36,929	37,185
4	92	3,5	12,25	42,875	150,06	322	1127	89,692	1,1598	11,459
5	94	4	16	64	256	376	1504	92,103	0,8521	0,9485
6	98	5	25	125	625	490	2450	96,021	24,237	8,6676

Продолжение таблицы 266

1	2	3	4	5	6	7	8	9	10	11
7	100	6	36	216	1296	600	3600	98,733	47,929	31,991
8	99	7	49	343	2401	693	4851	100,24	35,083	51,295
9	99	8	64	512	4096	792	6336	100,54	35,083	55,683
10	98	9	81	729	6561	882	7938	99,633	24,237	42,982
11	96	10	100	1000	10000	960	9600	97,521	8,5444	19,75
12	94	11	121	1331	14641	1034	11374	94,203	0,8521	1,2681
13	92	12	144	1728	20736	1104	13248	89,679	1,1598	11,546
Итого	1210	83	667,5	6141,5	60898,125	7877	63639,5	1210	536,92	510,26

Анализ исходных данных позволил установить, что зависимость криволинейная и может быть описана уравнением параболы 2-го порядка:

(76)

Требуется определить параметры уравнения связи и индекс корреляции.

Решение: Составим систему уравнений для нахождения параметров , , :

В систему уравнений подставим данные из табл. 266:

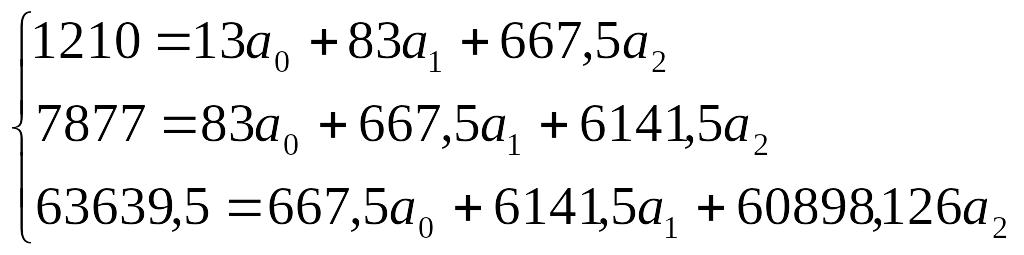
Разделим члены каждого уравнения на коэффициент при а_о

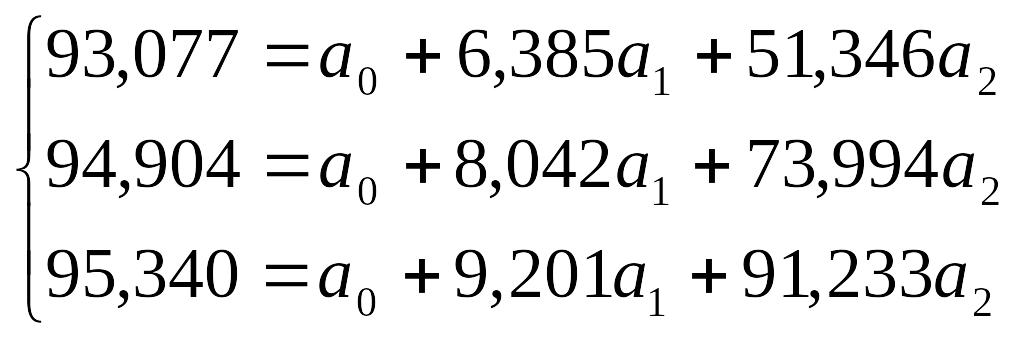
Теперь из второго уравнения вычтем первое, а из третьего - второе:

Освободимся от коэффициента при , для чего все члены уравнения разделим на коэффициент при :

Из первого уравнения вычтем второе и получим 0,727=-1,206 , отсюда а₂=-0,603. Подставим значения а₂ в уравнение 1,103= +13,668∙(-0,603); отсюда = 9,345. В уравнение 93,077 = + 6,385 + 51,346a₂ подставим значения найденных параметров и а₂:

93,077 = а₀ + 6,385∙9,345 + 51,346∙(- 0,603);

93,077 = + 59,668 - 30,962;

= 93,007 - 59,668 + 30,962;

= 64,371.

Следовательно, уравнение параболы второго порядка будет иметь следующий вид: = 64,371 + 9,345 - 0,603 .

Отрицательное значение а₂ показывает, что с увеличением возраста коров до определенного предела (6-го отела) удой возрастает на 9,345 % с каждым новым отелом, а затем после определенного предела (с 6-го отела до 12-го отела) начинает падать в среднем на 0,603 % .

Когда связь между нелинейная (в нашем случае - параболическая), для измерения тесноты связи используют корреляционное отношение, которое рассчитывается по формуле:

Полученный результат свидетельствует о наличии тесной связи между возрастом коров и их продуктивностью, так как 95,03 % вариации в продуктивности связано с возрастом данной группы коров.

Решим эту же задачу с помощью программы Statgraphics, используя в расчетах функцию Polynomial Regression (рис. 45).

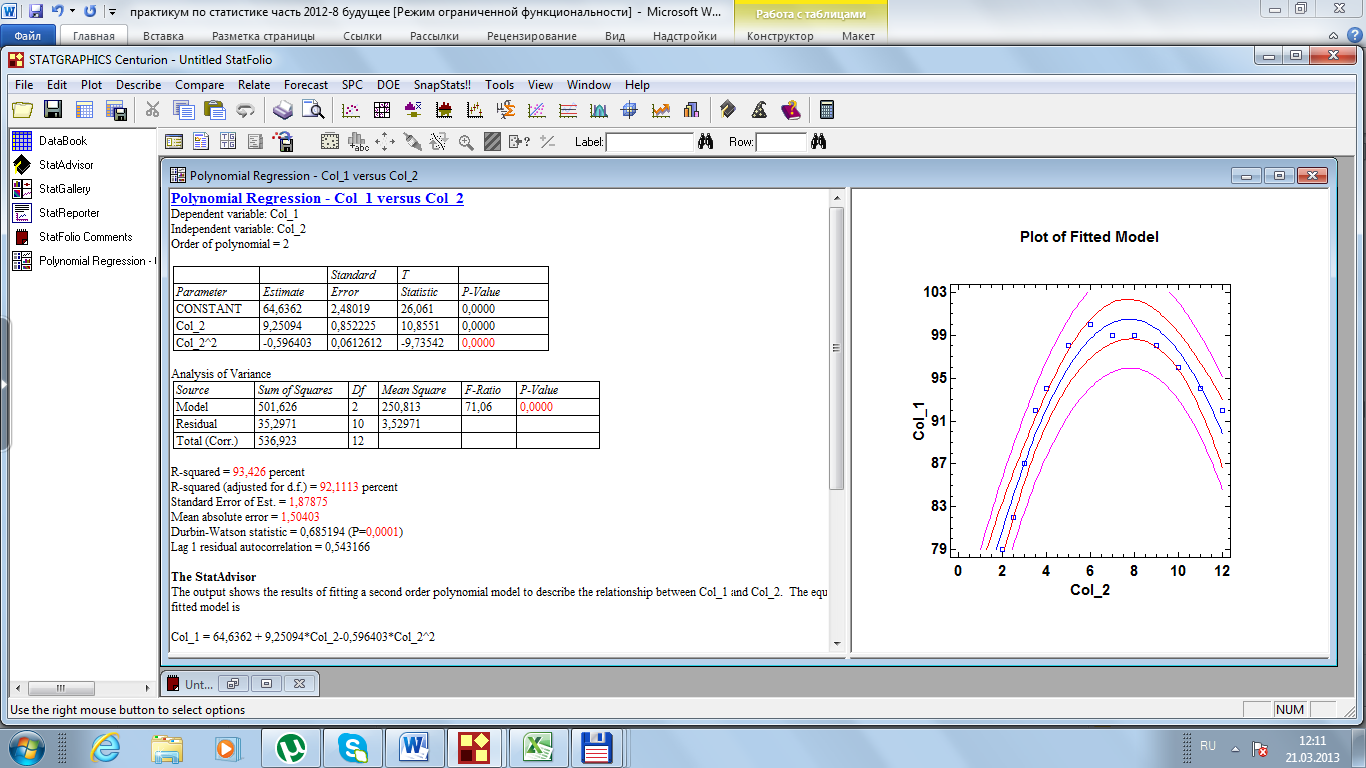
Рис. 45. Результаты расчетов

Уравнение парной криволинейной зависимости примет вид: .

Случайные ошибки параметров , , равны , , . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: , , . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости , т.е. с вероятностью 0,95 составит 2,2281, , т.е. с вероятностью 0,99 – 3,1693. Статистически значимыми здесь являются , , .

Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( , и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так , и То есть вероятность случайно получить такие значения t-критерия Стьюдента составляет 0,0000 %, что не превышает допустимый уровень значимости 5 %.

Чуть ниже на рис. 45 представлен расчет F-критерий Фишера, и он составляет 71,06. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

Отсюда же берем нескорректированный коэффициент детерминации , который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.

Задача 4. Имеются выборочные данные по 12 однородным предприятиям (табл. 267). Определите в программе Statgraphics уравнение регрессии, наиболее полно отражающее исходные данные. Оцените значимость параметров уравнения регрессии с помощью t-критерия Стьюдента и F-критерия Фишера.

Таблица 267 – Исходные данные

№ предприятия	Выпуск готовой продукции на одного рабочего, т	Электровооруженность труда на одного рабочего, кВтч
1	2	1
2	7	5
3	4	3
4	7	7
5	4	2
6	8	6
7	6	4
8	5	3
9	9	8
10	9	9
11	5	4
12	5	3

Построить однофакторную регрессионную модель.

Решение: воспользовавшись программой Statgraphics, получим следующие данные (табл. 268).

Таблица 268 – Уравнения регрессии, коэффициент детерминации и достоверность

№ п/п	Уравнение регрессии			P		P	F	P
1	2	3	4	5	6	7	8	9
1		90,68	4,86	0,007	9,86	0,0000	97,26	0,0000
2		86,59	14,01	0,0000	8,04	0,0000	64,58	0,0000
3		79,63	7,83	0,0000	6,25	0,0001	39,09	0,0001
4		59,81	7,92	0,0000	-3,86	0,0032	14,88	0,0032
5		92,27	-1,38	0,1965	10,93	0,0000	119,4	0,0000
6		93,50	-2,11	0,0608	11,99	0,0000	143,80	0,0000
7		92,39	5,64	0,0002	11,02	0,0000	121,49	0,0000
8		88,32	1,86	0,0932	8,70	0,0000	75,62	0,0000
9		90,09	-4,93	0,0006	9,53	0,0000	90,90	0,0000
10		91,44	3,01	0,0130	10,34	0,0000	106,89	0,0000
11		94,13	16,46	0,0000	12,66	0,0000	160,39	0,0000
12		94,14	10,30	0,0000	12,67	0,0000	160,63	0,0000
13		82,45	-1,43	0,1844	6,86	0,0000	47,00	0,0000
14		71,56	14,22	0,0000	-5,02	0,0005	25,17	0,0005
15		88,78	30,73	0,0000	-8,90	0,0000	79,15	0,0000
17		96,68	6,80	0,0000	17,08	0,0000	291,58	0,0000
18		55,25	7,34	0,0000	-3,51	0,0056	12,35	0,0056
19		79,81	9,12	0,0000	6,29	0,0001	39,54	0,0001
20		72,60	18,18	0,0000	5,15	0,0004	26,50	0,0004
21		63,14	11,73	0,0000	4,14	0,0020	17,3	0,0020
22		41,68	7,49	0,0000	-2,67	0,0234	7,15	0,0234
23		87,73	3,60	0,0048	8,46	0,0000	71,52	0,0000

Как видим из таблицы 5, 6, 8 и 13 уравнения отпадают, так как не соответствуют по уровню t-критерия Стьюдента. Наиболее полно отражает действительность 17 модель, так как коэффициент детерминации равен 96,68 %. Однако более точный выбор дал бы коэффициент апроксимации.