7. Механический расчет проводов о пределение расчетных условий проводов для линии ас240

Все линии выполнены проводом АС240. В соответствии с заданием электрическая сеть проектируется для II района гололедности с толщиной стенки гололеда c = 10 мм и III ветрового района со скоростным напором ветра g = 50 кГс/м² с температурами t_min = – 40 С, t_эксп = 0 С, t_max = 40 С. Температура образования гололеда t_г = – 5 С.

Исходные данные для определения удельных нагрузок выбираем из [7]: сечение алюминия 244 мм², сечение стали 31,7 мм², общее сечение провода F = 275,7 мм², диаметр провода d = 21,6 мм, масса 1 км G = 921 кг.

Определяем удельную нагрузку от собственной массы провода

.

Удельная нагрузка от массы гололеда

Нагрузка от массы провода с гололедом

.

Удельная нагрузка от ветра на провод без гололеда

,

где  = 0,783 при q = 50 кг/м² – коэффициент, учитывающий неравномерность давления ветра по пролету; = 1,1 при d > 20 мм – коэффициент лобового сопротивления

.

Удельная нагрузка от ветра на провод с гололедом

.

Принимаем  = 1 при скоростном напоре менее 27 кгс/м² и = 1,1, тогда

.

Удельная нагрузка от ветра и веса провода без гололеда

.

Удельная нагрузка от ветра и веса провода с гололедом

.

П о таблицам ПУЭ выбираем для провода АС240 модуль упругости ; температурный коэффициент линейного удлинения ; допускаемые напряжения при наибольшей нагрузке _г = 12,2 кГс/мм², при низшей температуре _н = 10,7 кГс/мм², при среднегодовой температуре _э = 7,25 кГс/мм². Определяем критические пролеты по формулам [9]:

,

,

.

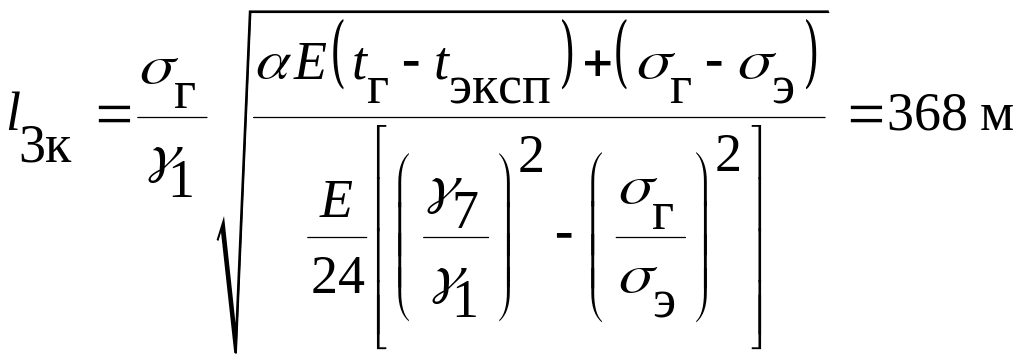Задаемся расчетным пролетом l = 380 м. При соотношении пролетов расчетным критическим пролетом является и исходными напряжениями и [9]. Так как заданный пролет больше , то необходимо использовать уравнение состояния провода в пролете, исходящее из напряжений и нагрузок при гололеде и ветре

.

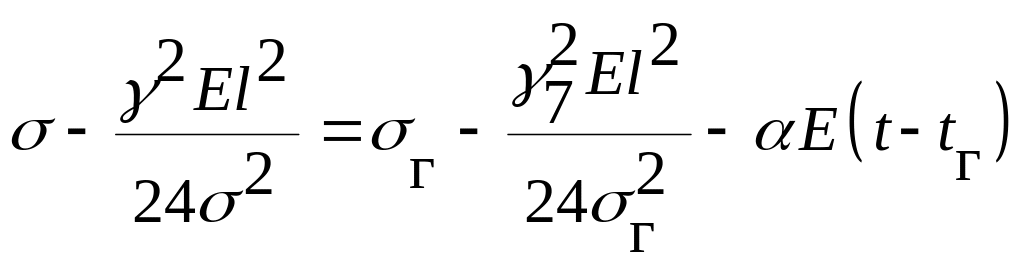Рассчитываем режим, при котором провода покрыты гололедом, , ветра нет

.

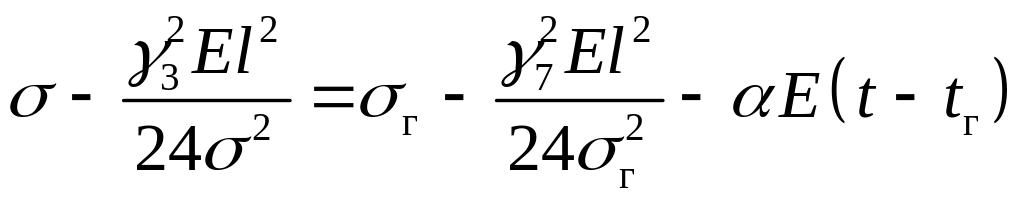После подстановки и преобразований получим

.

Корнем этого кубического уравнения можно считать

Вычислим стрелу провеса для этого режима

.

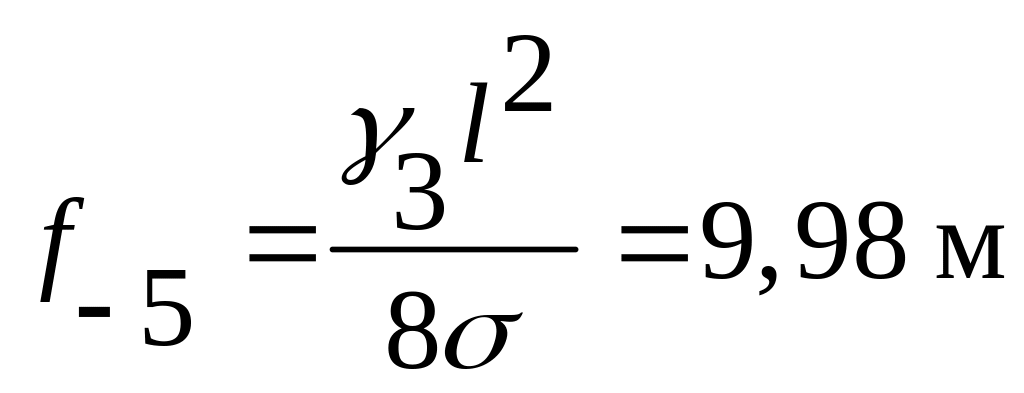
Рассчитаем прочие режимы:

при без гололеда с ветром ;

при без ветра и гололеда ;

при , ветра и гололеда нет ;

при низшей температуре без гололеда и ветра ;

при максимальной температуре без гололеда и ветра .

Выполнив механический расчет, убедились, что ни в одном из рассчитанных режимов напряжение в материале провода не достигло допустимых значений. Максимальное значение стрелы провеса провода = 10,2 м достигается при максимальной температуре.

0. Выбор типа промежуточной опоры для рассчитанного пролета.

Подсчитываем расчетную высоту опоры от поверхности земли до нижней траверсы

,

где h – наименьшее расстояние от проводов воздушных линий до поверхности земли,  – высота гирлянды изоляторов. Для воздушной линии 220 кВ можно принять  = 2,47 м.

При напряжении линии 220 кВ h = 8 м в населенной местности. При этих условиях = 20,67 м.

Выбираем по [7] промежуточную железобетонную опору типа ПБ 220-3 с = 25,5 м. Выбранная опора длиннее расчетной на 4,83 м. Для того, чтобы расстояние h осталось прежним, надо увеличить расчетный пролет так, чтобы f¹_max =Н_действ – h - λ.

Новому значению f¹_max соответствует скорректированный расчетный пролет l¹, величину которого можно определить из соотношения

.

В начале и в конце каждой линии, вблизи приемных порталов подстанций, устанавливаются концевые опоры.