2 Задания для лабораторной работы
1.Записать каноническое уравнение и определить вид кривой. Записать уравнения директрис, асимптот (если это необходимо). Определить координаты фокусов, вершин, центров и другие параметры полученной кривой.
1.1 |
4x2+8x+y2-2y-11=0 |
1.2 |
x2+y2-4x+2y-4=0 |
|
|
|
|
1.3 |
9x2+4y2-24y=0 |
1.4 |
x2+4y2-6x+5=0 |
|
|
|
|
1.5 |
16x2+9y2-32x-36y-92=0 |
1.6 |
4x2+y2-8x-4y-8=0 |
|
|
|
|
1.7 |
x2+4y2-4x-32=0 |
1.8 |
x2+25y2+2x+100y-124=0 |
|
|
|
|
1.9 |
x2+4x+4y2-32=0 |
1.10 |
x2+y2+2x-4y-4=0 |
|
|
|
|
1.11 |
y2-x-2y+4=0 |
1.12 |
y2-6x-6y+21=0 |
|
|
|
|
1.13 |
x2-2x-y-5=0 |
1.14 |
x2-8x-8y+24=0 |
|
|
|
|
1.15 |
2y2-x-12y+14=0 |
1.16 |
y2+x-6=0 |
|
|
|
|
1.17 |
x+y2-2y-1=0 |
1.18 |
4x2-y-8x+7=0 |
|
|
|
|
1.19 |
9x2-y2+36x+45=0 |
1.20 |
4x2-25y2-8x-100y-196=0 |
|
|
|
|
1.21 |
9x2-4y2+18x+16y-43=0 |
1.22 |
x2-4y2-6x-24y-31=0 |
|
|
|
|
1.23 |
x2-4y2—2x+8y-19=0 |
1.24 |
4y2-x2+4x+12=0 |
|
|
|
|
1.25 |
-25x2+25y2—100x+100y-225=0 |
1.26 |
5x2+5y2-30x+20y+20=0 |
|
|
|
|
1.27 |
9x2-4y2+72x-16y+92=0 |
1.28 |
9x2-y2+36x=0 |
|
|
|
|
1.29 |
9x2-y2-54x-4y+41=0 |
1.30 |
9x2+y2+2y-35=0 |
2. Записать каноническое уравнение поверхности. Определить ее вид. Построить тело, ограниченное указанными поверхностями.
2.1 |
4x2-y2+2z2-16x+12=0, y=0, y=3 |
2.2 |
9x2-2y2+4z2+18x-8z+49=0, y=6 |
|
|
|
|
2.3 |
9x2+4y2-z2-18x-16y+61=0, z=12 |
2.4 |
2x2+8y2-8z=0, z=4 |
|
|
|
|
2.5 |
4x2+y2-z2+16x+12=0, z=0, z=2 |
2.6 |
4x2+9y2-36z2+8x+144z-176=0, z=3, z=0 |
|
|
|
|
2.7 |
4x2+9y2-36z2+8x+144z-176=0, y=0, y=2 |
2.8 |
x2-9y2-2x-z+1=0, z=3 |
|
|
|
|
2.9 |
9x2-16y2+9z2+144=0, y=0 |
2.10 |
4x2+9y2-z2+36=0, z=12 |
|
|
|
|
2.11 |
9x2+16y2+9z2-144=0, x=0, x=2 |
2.12 |
9x2+9y2+36z2-72z=0, z=1, z=2 |
|
|
|
|
2.13 |
x2+9y2-2x-8=0, z=y, y=0 |
2.14 |
-4x2+9y2+z2+36=0, x=8 |
|
|
|
|
2.15 |
9x2+4y2-z2-2x-16y-11=0, x=2, x=1 |
2.16 |
4x2+9y2-36z2-24x=0, z=0, z=4 |
|
|
|
|
2.17 |
2x2-8y2-z=0, z=4 |
2.18 |
-4x2+16y2+z2-32y=0, x=0, x=2 |
|
|
|
|
2.19 |
x2+4y2+6x-8y-4z+13=0, z=4 |
2.20 |
x2+y2+z2-36=0, x=0, x=2 |
|
|
|
|
2.21 |
2x2+18y2-z=0, z=18 |
2.22 |
4x2+16y2+z2-32y=0, z=-2, z=2 |
|
|
|
|
2.23 |
4x2+16y2+z2+32y=0, z=0, z=3 |
2.24 |
4x2+9y2+8x+36y-z2+4=0, z=0, z=4 |
|
|
|
|
2.25 |
16x2-9y2+9z2=0, y=0, y=3 |
2.26 |
9x2+25y2-225z2-225=0, z=0, z=2 |
|
|
|
|
2.27 |
y2-4x2+16z2=0, x=0, x=2 |
2.28 |
9x2+y2-18x=0, z=4, z=1 |
|
|
|
|
2.29 |
4x2+9y2-z2-8x-36y+4=0, z=0, z=2 |
2.30 |
4x2-4y2-4z2-16x-32=0 z=0, z=3 |
Построить кривую, заданную в полярных координатах по точкам, начиная от
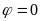до
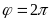с шагом
.
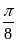Найти уравнение заданной кривой в
декартовой системе координат, у которой
начало совпадает с полюсом, а положительная
полуось абсцисс - с полярной осью.
3.1 |
r= |
3.1 |
r= |
|
|
|
|
3.3 |
r= |
3.4 |
r= |
|
|
|
|
3.5 |
r=a |
3.6 |
r= |
|
|
|
|
3.7 |
r= |
3.8 |
r= |
|
|
|
|
3.9 |
r2= |
3.10 |
r2= |
|
|
|
|
3.11 |
r=5 |
3.12 |
r= |
|
|
|
|
3.13
|
r= |
3.14 |
r= |
|
|
|
|
3.15 |
r= |
3.16 |
r= |
|
|
|
|
3.17 |
r= |
3.18 |
r= |
|
|
|
|
3.19 |
r= |
3.20 |
r= |
|
|
|
|
3.21 |
r= |
3.22 |
r= |
|
|
|
|
3.23 |
r= |
3.24 |
r= |
|
|
|
|
3.25 |
r= |
3.26 |
r= |
|
|
|
|
3.27 |
r= |
3.28 |
r= |
|
|
|
|
3.29 |
r= |
3.30 |
r= |
|
|
|
|
