37. Поточные шифры на регистрах сдвига с линейной обратной связью (рслос): Теоретическая основа
Есть несколько причин использования линейных регистров сдвига в криптографии:
высокое быстродействие криптографических алгоритмов
применение только простейших операций сложения и умножения, аппаратно реализованных практически во всех вычислительных устройствах
хорошие криптографические свойства (генерируемые последовательности имеют большой период и хорошие статистические свойства)
легкость анализа с использованием алгебраических методов за счет линейной структуры
Определение: Регистр сдвига с линейной обратной связью длины L состоит из L ячеек пронумерованных ,каждая из которых способна хранить 1 бит и имеет один вход и один выход; и синхросигнала (clock), который контролирует смещение данных. В течение каждой единицы времени выполняются следующие операции:
содержимое ячейки формирует часть выходной последовательности;
содержимое -той ячейки перемещается в ячейку для любого , .
новое содержимое ячейки определяется битом обратной связи, который вычисляется сложением по модулю 2 с определёнными коэффициентами битов ячеек .
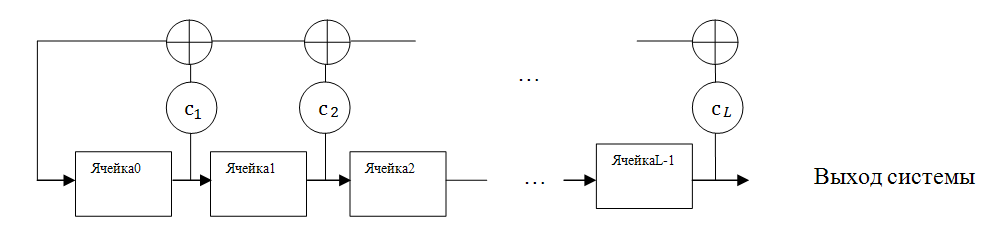
Регистр сдвига с линейной обратной связью.
На первом
шаге:
На втором шаге:
Следующее
соотношение описывает в общем виде
работу РСЛОС:
Если мы запишем
во все ячейки биты равны нулю, то система
будет генерировать последовательность,
состоящую из всех нулей. Если записать
ненулевые биты, то получим полубесконечную
последовательность. Последовательность
определяется коэффициентами
Посмотрим,
каким может быть период
такой системы:
Число ненулевых
заполнений: Значит, .
После возникновения
одного заполнения, которое было раньше,
процесс начнёт повторяться. Процесс
заполнения регистра, как показано выше,
представим линейным разностным
уравнением. Перенесём все члены в одну
часть равенства, получим:
.
Обозначим:
. Тогда:
Важным свойством
этого многочлена является -
приводимость.
Определение:
Многочлен
называется приводимым,
если он может быть представлен как
произведение двух многочленов меньших
степеней с коэффициентами из данного
поля (в нашем случае с двоичными
коэффициентами). Если такое представление
не имеет место, то многочлен называется
неприводимым.
Если
многочлен является неприводимым и
примитивным,
то период будет совпадать с максимально
возможным периодом, равным
Пример.
Пример: Возьмём неприводимый примитивный многочлен Этот многочлен можно записать, как – выписаны степени, при которых стоят ненулевые коэффициенты. Запишем в исходном состоянии в ячейки и определим длину периода генератора:
Таблица. Определение периода генератора
Обратная связь |
Ячейка0 |
Ячейка1 |
Ячейка2 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
Период генератора равен На выходе генератора буде последовательность: Приведём примеры некоторых примитивных многочленов по модулю 2: