Кодовая скорость (к выкалыванию)

Кодовая скорость — отношение длины кодового блока на входе к длине преобразованного кодового блока на выходе кодера.

В отсутствие перфоратора (см. рис. 1) исходная последовательность   мультиплексируется с последовательностями проверочных бит  , образуя кодовое слово, подлежащее передаче по каналу. Тогда значение кодовой скорости на выходе турбо-кодера

Для увеличения кодовой скорости применяется выкалывание (перфорация) определённых проверочных битов выходной последовательности. Таким образом кодовая скорость возрастает до

 , где  , причём   может быть дробным, если число оставшихся после перфорации проверочных бит не кратно  .

Если учесть, что турбо-коды оперируют с блоками большой длины c  , то  , и кодовая скорость равна

Из приведённых формул видно, что с помощью перфоратора, выкалывая разное число проверочных бит, возможно регулирование кодовой скорости. То есть можно построить кодер, адаптирующийся к каналу связи. При сильном зашумлении канала перфоратор выкалывает меньше бит, чем вызывает уменьшение кодовой скорости и рост помехоустойчивости кодера. Если же канал связи хорошего качества, то выкалывать можно большое число бит, вызывая рост скорости передачи информации.

Функция Уолша

Функциями Уолша называется семейство функций, образующих ортогональную систему, принимающих значения только 1 и −1 на всей области определения.

В принципе, функции Уолша могут быть представлены в непрерывной форме, но чаще их определяют как дискретные последовательности из   элементов. Группа из   функций Уолша образует матрицу Адамара.

Функции Уолша получили широкое распространение в радиосвязи, где с их помощью осуществляется кодовое разделение каналов (CDMA), например, в таких стандартах сотовой связи, как IS-95, CDMA2000 или UMTS.

Система функций Уолша является ортонормированным базисом и, как следствие, позволяет раскладывать сигналы произвольной формы в обобщённый ряд Фурье .

Обозначение

Пусть функция Уолша определена на интервале [0, T]; за пределами этого интервала функция периодически повторяется. Введём безразмерное время  . Тогда функция Уолша под номером k обозначается как  . Нумерация функций зависит от метода упорядочения функций. Существует упорядочение по Уолшу — в этом случае функции обозначаются так, как описано выше. Также распространены упорядочения по Пэли ( ) и по Адамару ( ).

Относительно момента   функции Уолша можно разделить на чётные и нечётные. Они обозначаются как   и   соответственно. Эти функции аналогичны тригонометрическим синусам и косинусам. Связь между этими функциями выражается следующим образом:

Формирование

Существует несколько способов формирования. Рассмотрим один из них, наиболее наглядный: Матрица Адамара может быть сформирована рекурсивным методом с помощью построения блочных матриц по следующей общей формуле:

Так может быть сформирована матрица Адамара длины  :

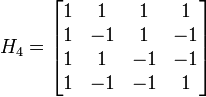
Каждая строка Матрицы Адамара и является функцией Уолша.

В данном случае функции упорядочены по Адамару. Номер функции по Уолшу вычисляется из номера функции по Адамару путём перестановки бит в двоичной записи номера в обратном порядке с последующим преобразованием результата из кода Грея.

Свойства

1. Ортогональность

Скалярное произведение двух разных функций Уолша равно нулю:

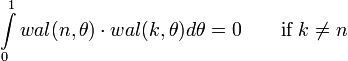
Пример

Допустим, что n = 1, k = 3 (см. выше). Тогда,

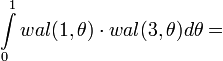
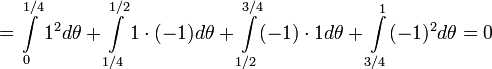
2. Мультипликативность

Произведение двух функций Уолша даёт функцию Уолша.

где   — сложение по модулю 2 номеров в двоичной системе.

Пример

Допустим, что n = 1, k = 3. Тогда,

В результате умножения получим:

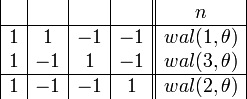
Преобразование Уолша-Адамара

Является частным случаем обобщённого преобразования Фурье, в котором базисом выступает система функций Уолша.

Обобщённый ряд Фурье представляется формулой:

где   это одна из базисных функций, а   — коэффициент.

Разложение сигнала по функциям Уолша имеет вид:

В дискретной форме формула запишется следующим образом:

Определить коэффициенты   можно, осуществив скалярное произведение раскладываемого сигнала на соответствующую базисную функцию Уолша:

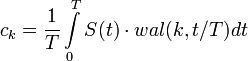
Следует учитывать периодический характер функций Уолша. Существует также быстрое преобразование Уолша.

Алгоритм свёрточного декодирования Витерби

В 1967 году Витерби (Viterbi) разработал и проанализировал алгоритм, в котором реализуется декодирование, основанное на принципе максимального правдоподобия. В алгоритме уменьшается вычислительная нагрузка за счёт использования особенностей структуры конкретной решётки кода. Преимущество декодирования Витерби, по сравнению с декодированием по методу полного перебора, заключается в том, что сложность декодера Витерби не является функцией количества символов в последовательности кодовых слов. Алгоритм включает в себя вычисление меры подобия (или расстояния), между сигналом, полученным в момент времени t1, и всеми путями решётки, входящими в каждое состояние в момент времени ti. В алгоритме Витерби не рассматриваются те пути решётки, которые, согласно принципу максимального правдоподобия, заведомо не могут быть оптимальными. Если в одно и то же состояние входят два пути, выбирается тот, который имеет лучшую метрику; такой путь называется выживающим. Отбор выживающих путей выполняется для каждого состояния. Таким образом, декодер углубляется в решётку, принимая решения путём исключения менее вероятных путей. Предварительный отказ от маловероятных путей упрощает процесс декодирования. В 1969 году Омура (Omura) показал, что основу алгоритма Витерби составляет оценка максимума правдоподобия. Отметим, что задачу отбора оптимальных путей можно выразить как выбор кодового слова с максимальной метрикой правдоподобия или минимальной метрикой расстояния.

Сущность метода

Наилучшей схемой декодирования корректирующих кодов является декодирование методом максимального правдоподобия, когда декодер определяет набор условных вероятностей P(r/Ui) , соответствующих всем возможным кодовым векторам Ui, и решение принимает в пользу кодового слова, соответствующего максимальному P(r/Ui) . Для двоичного симметричного канала без памяти (канала, в котором вероятности передачи 0 и 1, а также вероятности ошибок вида 0 -> 1 и 1 -> 0 одинаковы, ошибки в j-м и i-м символах кода независимы) декодер максимального правдоподобия сводится к декодеру минимального хеммингова расстояния. Последний вычисляет расстояние Хемминга между принятой последовательностью r и всеми возможными кодовыми векторами Ui и выносит решение в пользу того вектора, который оказывается ближе к принятому. Естественно, что в общем случае такой декодер оказывается очень сложным и при больших размерах кодов n и k практически нереализуемым. Характерная структура сверточных кодов (повторяемость структуры за пределами окна длиной n) позволяет создать вполне приемлемый по сложности декодер максимального правдоподобия.

Принцип работы декодера

На вход декодера поступает сегмент последовательности r длиной b , превышающей кодовую длину блока . Назовем b окном декодирования. Сравним все кодовые слова данного кода (в пределах сегмента длиной b) с принятым словом и выберем кодовое слово, ближайшее к принятому. Первый информационный кадр выбранного кодового слова принимается в качестве оценки информационного кадра декодированного слова. После этого в декодер вводится n0 новых символов, а введенные ранее самые старые n0 символов сбрасываются, и процесс повторяется для определения следующего информационного кадра. Таким образом, декодер Витерби последовательно обрабатывает кадр за кадром, двигаясь по решетке, аналогичной используемой кодером. В каждый момент времени декодер не знает, в каком узле находится кодер, и не пытается его декодировать. Вместо этого декодер по принятой последовательности определяет наиболее правдоподобный путь к каждому узлу и определяет расстояние между каждым таким путем и принятой последовательностью. Это расстояние называется мерой расходимости пути. В качестве оценки принятой последовательности выбирается сегмент, имеющий наименьшую меру расходимости. Путь с наименьшей мерой расходимости называется выжившим путем.