3.2. Задача о назначениях

Средство Excel Поиск решения можно использовать также для решения еще одной экономической задачи, задачи о назначениях. Рассмотрим пример ее решения. Пусть четверо рабочих могут выполнять четыре вида работ. Стоимости с_ij выполнения i-м рабочим j-ого вида работы приведены в таблице 3.2.

Таблица 3.2. Стоимость выполнения работ

Робітники	Види робіт
	1	2	3	4
1	8	6	2	5
2	5	2	9	8
3	3	8	1	9
4	1	4	2	3

Необ­ходимо составить такой план выполнения работ, чтобы все работы были вы­полнены, а каждый рабочий был загружен только на одной работе. Суммар­ная стоимость выполнения всех работ должна быть минимальной.

Данная модель является сбалансированной, т. е. число работ совпадает с чис­лом рабочих. В случае несбалансированной модели перед началом решения ее необходимо сбалансировать, введя недостающее число фиктивных строчек или столбцов с достаточно большими штрафными стоимостями работ.

При решении этой задачи удобно использовать следующую таблицу x_i : ее строки – номера рабочих, а столбцы – номера работ. Тогда если i-й работник выполняет i–ю работу, то поместить в ячейку таблицы ij x_ij=1. Если нет, то x_ij=0. Иначе порядок заполнения таблицы можно представить так:

Тогда суммарную стоимость выполнения всех работ можно найти из выражения

.

Неизвестные в данной задаче должны удовлетворять следующим ограничениям:

Для решения этой задачи с помощью средства Поиск решения введем данные, как показано на рисунке 3.4.

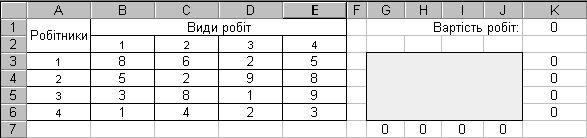
Рис. 3.4. Исходные данные задачи о назначениях

В ячейку K1 введем целевую функцию {=СУИМПРОИЗВ(G3:J6;B3:E6)} вычисляющую стоимость работ. В ячейку G7 необходимо ввести формулу {=СУММ(G3:G6)} и скопировать ее до ячейки J7,а в ячейку K3 необходимо ввести формулу {=СУММ(G3:J3)} и скопировать ее до ячейки K6. Тогда в ячейках K3:K6, G7:J7 будут заданы левые части ограничений.

Затем необходимо выбрать команду Сервис, Поиск решения и заполнить открывшееся диалоговое окно Поиск решения, как показано на рис. 3.5.

В диалоговом окне Параметры поиска решения важно устано­вить флажок Линейная модель. После нажатия кнопки Выполнить средство поиска решений найдет оптимальный план выполнения работ. Результаты решения задачи о назначениях представлены на рис.3.6.

Рис. 3.5. Диалоговое окно Поиск решения задачи о назначениях

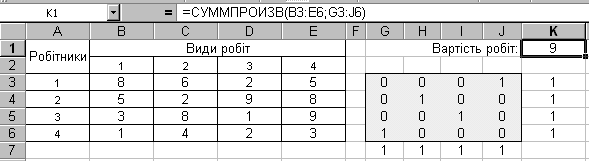
Рис. 3.6. Оптимальный план работ в задаче о назначениях

3.3. Линейная оптимизационная задача

В данном разделе рассмотрим, как с помощью средства Поиск решения решаются линейные оптимизационные задачи на примере трех типичных ситуаций: планирование производства, составление сплавов или смесей и планирование штатного расписания.