Обработка экономической информации в MS EXCEL

Использование механизмов Excel в типовых экономических задачах

Содержание

Введение

1. Решение линейных уравнений и их систем

1.1. Решение уравнений

1.2. Решение систем линейных уравнений

1.3. Решение систем нелинейных уравнений

2. Традиционные экономические задачи

2.1. Транспортная задача

2.2. Задача о назначениях

2.3. Линейная оптимизационная задача

2.3.1. Планирование производства красок

2.3.2. Определение состава сплавов

2.3.3. Планирование штатного расписания

3. Построение уравнения регрессии

Список рекомендованной литературы

1. Решение линейных уравнений и их систем

2.1. Решение уравнений

При решении практических задач возникает необходимость подбора одного из параметров экономической модели для достижения определенного значения некоторой сложной экономической функции f(x). Фактически необходимо решить уравнение f(x)=A относительно параметра х. В Excel решение экономических задач реализовано как Подбор параметра.

Пример. Задача составления штатного расписания.

Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующая хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 10 000 грн. Необходимо определить, какими должны быть оклады сотрудников больницы.

Обозначим наименьший оклад, оклад санитарки, переменной С. Тогда оклады остальных сотрудников могут быть найдены по формуле: A_i*С+В_i, где А_i и В_i - коэффициенты, определенные на рабочем листе Excel (см. рис. 2.1). При этом фонд заработной платы вычисляется по выражению

N₁*A₁*C+N₂*(A₂*C+B₂)+...+N₈*(A₈*C+B₈) = 10000,

где N_i - число сотрудников i-той должности (i=1,2,…,8).

Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С. Для его решения необходимо ввести исходные данные в рабочий лист электронной таблицы, как показано ниже.

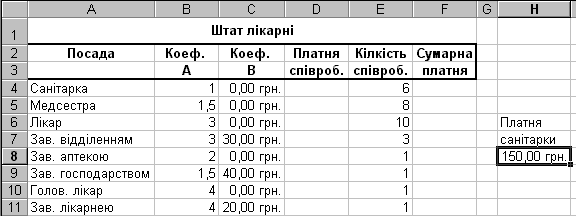
Рис. 2.1.

Ввод формул осуществляется следующим образом:

• ввести формулу для заработной платы в ячейку D4 (=B4*$H$8+C4) и скопировать ее до ячейки D11;

• ввести формулу для заработной платы всех рабочих данной должности в ячейку F4 (=D4*E4) и скопировать ее до ячейки F11;

• вычислить сумму значений диапазона ячеек F4:F11 в ячейке F12; полученный результат - суммарный фонд заработной платы больницы;

• активизировать команду Подбор параметра из меню Сервис;

• в поле Установить в ячейке появившегося окна ввести ссылку на ячейку F12, содержащую формулу;

• в поле Значение набрать искомый результат 10000;

• в поле Изменяя значение ячейки ввести ссылку на изменяемую ячейку H8 и нажать на кнопку ОК.

Результат решения задачи показан на рис.2.2.

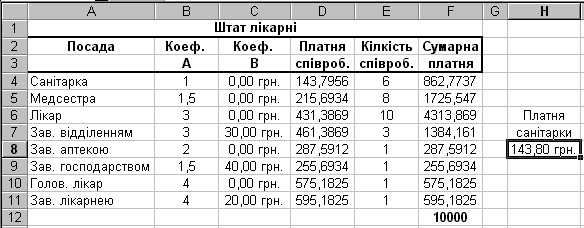
Рис.2.2

2.2. Решение систем линейных уравнений

Некоторые экономические задачи сводятся к решению систем линейных уравнений, которые могут быть решены в Excel следующим образом:

• С помощью численных методов Гаусса, Жордана и подобных им.

• При помощи специальных функции Excel для работы с матрицами.

• При помощи механизма Excel Поиск решения.

Второй путь является наиболее эффективным.

В Excel имеются следующие специальные функции работы с матрицами:

МОБР обратная матрица;

МОПРЕД определитель матрицы;

МУМНОЖ матричное произведение двух матриц;

ТРАНСП транспонированная матрица.

Система линейных уравнений в матричной форме может быть записана в виде АХ = В, где А – матрица коэффициентов, В – вектор-столбец свободных членов, X– вектор-столбец неизвестных. Если матрица А невырожденная (det A  0), тогда решение может быть представлено в виде X=А^-1В, где А^-1 – матрица обратная А. Для решения системы уравнений необходимо выделить под вектор решений X диапазон ячеек и ввести в него формулу {=МУМНОЖ(МОБР(<Матрица коэффициентов А>);<Матрица свободных членов В>)}.

Пример.

Задана система линейных уравнений с тремя неизвестными, матрица коэффициентов А которой записана в ячейки B1:D3, а свободные члены – в ячейки F1:F3 (рис. 2.3). Перед вводом формулы необходимо выделить диапазон H1:H3 под решение системы. Затем ввести формулу {=МУМНОЖ(МОБР(B1:D3);F1:F3)} и нажать комбинацию клавиш <Сtrl>+<Shift>+<Enter> (если нажать клавишу <Enter> в ячейке H1 появится сообщение #знач !). В результате в ячейках H1:H3 будет представлено решение системы.

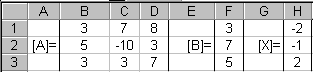
Рис. 2.3. Решение системы линейных уравнений

2.3. Решение систем нелинейных уравнений

Механизм поиска решений также позволяет нахо­дить решения систем нелинейных уравнений.

Пример. Решить следующую систему уравнений

Известно, что решение данной системы уравнений совпадает с решением следующего уравнения с двумя неиз­вестными:

(x² + у² - 2)² + (3х + 2у - 2)² = 0.

Численное решение нелинейной задачи зависит от начального прибли­жения, удачный подбор которого очень важен. Одним из способов локализации корней является табуляция. Excel располагает механизмом Таблица подстановки, позволяющим решать подобную задачу. Результат табуляции по переменным х и у на отрезке [-3, 3] с шагом 1,5 приведен на рис. 2.4.

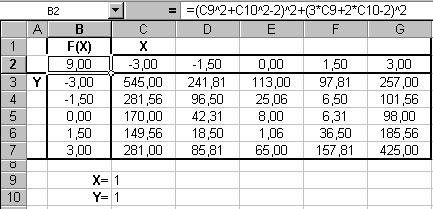
Рис. 2.4. Результат табуляции уравнения

В ячейки С9 и С10 помещены значения х и у, а в ячейку В2 - соответствующее выражение, вычисляющее левую часть уравнения при значениях х и у из диапазонов C2:G2 и B3:B7 соответственно. Из рис. 2.4 видно, что за начальное приближение к корню можно выбрать следующие пары значений (0; 1,5) – ячейка Е6, (1,5; 0) – ячейка F5. Можно убедиться, что две последние пары начальных приближений с помощью, средства поиска ре­шений будут приводить к нахождению одного и того же решения.

Для нахождения корня в открывшемся диалоговом окне Поиск решения в поле Установить целевую ячейку необходимо ввести адрес ячейки, в которой задана функция ($B$2). В поле Изменяя ячейки - адреса ячеек C9;C10. В группе Равной устанавливается переключатель в положение Значению, в поле ввода которого вводится 0. При этом в диалоговом окне Параметры поиска решения флажок Линейная модель должен быть снят.

После нажатия на кнопку Выполнить в ячейках C9 и C10 помещается решение. В данном случае это будут значения -0,25995; 1,390099. Если в диалоговом окне Результаты поиска решения в качестве типа отчета выбрать Результаты, Excel открывает дополнительный лист, представленный на рис. 2.5.

Рис. 2.5. Отчет по результатам решения системы уравнений

3.