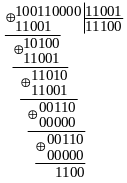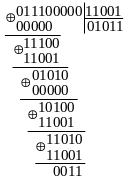3.4. Методичні вказівки до побудови пристроїв кодування та декодування циклічних кодів

Обчислення остач від ділення многочленів на утворюючий многочлен коду виконується в пристроях кодування та декодування за допомогою багатотактних перемикальних схем або фільтрів Хаффмена, які складаються з елементів затримки та суматорів за модулем 2.

Для виявлення закономірностей і методики побудови таких схем розглянемо процес ділення многочлена на многочлен. Нехай потрібно розділити многочлен на многочлен . Виконаємо ділення у стовпчик:

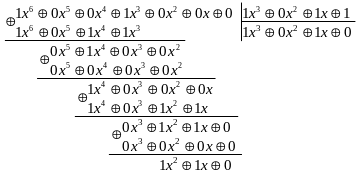
Ділення проводиться звичайним способом, але нижній рядок повинен відніматися з верхнього за модулем 2, що еквівалентно додаванню за модулем 2. Якщо замість многочленів використати набори їх коефіцієнтів, процедура ділення може бути записана компактніше:

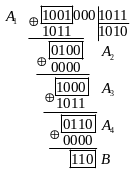
Звідси видно, що алгоритм знаходження остачі полягає в наступному: на ‑му кроці до набору , отриманого після попереднього кроку, додається за модулем 2 набір, що збігається з дільником, якщо лівий розряд у дорівнює 1, або нульовий набір, якщо цей розряд дорівнює 0. Результатом кроку є набір , утворений із цієї суми відкиданням лівого розряду (рівного 0) і дописуванням чергового розряду з діленого. На останньому кроці виходить набір коефіцієнтів остачі від ділення.

Послідовність операцій, розглянута в даному прикладі, може бути виконана регістром із трьох елементів затримки (степінь многочлена-дільника дорівнює трьом) і двох суматорів за модулем 2, що відповідають одиничним коефіцієнтам при й у дільнику. Суматор для додавання старшого розряду дільника зі старшим розрядом набору не потрібний, оскільки результат додавання завжди дорівнює нулю.

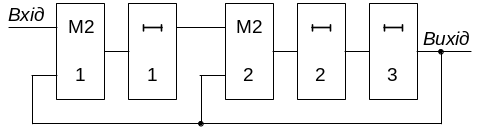
Рис. 3.1. Схема для ділення на многочлен

Схема для ділення на зображена на рис. 3.1. Передбачається, що всі елементи затримки, що утворюють регістр зсуву, синхронізуються однією послідовністю тактових імпульсів (ТІ). Ланцюг подачі цих імпульсів на схемі не показаний. Значення виходу елемента затримки безпосередньо після надходження ‑го ТІ збігається зі значенням на його вході безпосередньо після надходження ‑го ТІ. Суматори за модулем 2 вважаються безінерційними. На вхід схеми послідовно надходять коефіцієнти діленого, починаючи з коефіцієнта при старшому степені . Коефіцієнти частки з'являються на виході із затримкою у тактових інтервали. Остача буде знаходитися в регістрі по завершенні процесу ділення. У табл. 3.5 наведені стани виходів елементів затримки (ЕЗ) регістра при діленні на многочлена . У примітці зазначена відповідність елементів схеми діленню у стовпчик. Перші три такти не мають аналогії діленню у стовпчик; протягом цих тактів елементи діленого заповнюють регістр. Безпосередньо процес ділення починається із приходом 4‑го ТІ й закінчується з надходженням 7‑го ТІ. Між 7‑м й 8‑м тактовими імпульсами в регістрі знаходиться остача від ділення. З 8‑го ТІ в табл. 3.5 представлена робота схеми ділення в автономному режимі, коли на її вхід надходять "нулі". У цьому режимі стани схеми змінюються з періодом у тактових інтервалів і на виходах ЕЗ протягом періоду мають місце всі двійкові послідовності довжиною за винятком нульової послідовності (у табл. 3.5 представлені два періоди роботи схеми). Схема ділення, що працює в автономному режимі, використовується в декодері, що виправляє помилки (будемо називати її в цьому випадку генератором синдрому).

В загальному випадку схема ділення на многочлен степеня буде мати вигляд, показаний на рис. 3.2. Колами зазначені схеми множення на коефіцієнти . Очевидно, для двійкових кодів для множення на коефіцієнт, рівний 1, потрібна наявність зв'язку; якщо коефіцієнт дорівнює 0, зв'язок і відповідний йому суматор відсутні.

Схема такого типу може використовуватися як у кодері, так й у декодері. Однак, якщо її використати в кодері, то між надходженням на його вхід останнього інформаційного символу й завершенням формування остачі (тобто перевірочних символів) буде мати місце затримка в тактових інтервалів. Оскільки при видачі в канал зв'язку розрив між інформаційними й перевірочними символами зазвичай неприпустимий, у схемі кодера необхідно мати регістр із ЕЗ для затримки інформаційних символів на тактів. Виключити такий регістр дозволяє використання для обчислення остачі схеми, показаної на рис. 3.3. У цій схемі відсутній етап заповнення регістра коефіцієнтами діленого, тому процес обчислення остачі починається безпосередньо з моменту надходження коефіцієнта діленого при старшому степені . Через тактів у регістрі буде знаходитися остача від ділення. Така схема дає правильну остачу від ділення в тому випадку, якщо в діленому коефіцієнти при всіх молодших степенях є нулями. Тому в кодері, де така умова завжди виконується, її можна використовувати.

Таблиця 3.5
Номер ТІ	Вхід	Виходи ЕЗ			Примітка
		1	2	3
	1	0	0	0
1
	0	1	0	0
2
	0	0	1	0
3
	1	0	0	1	A1
4
	0	0	1	0	A2
5
	0	0	0	1	A3
6
	0	1	1	0	A4
7
	0	0	1	1	B
8
	0	1	1	1
9
	0	1	0	1
10
	0	1	0	0
11
	0	0	1	0
12
	0	0	0	1
13
	0	1	1	0
14
	0	0	1	1
15
	0	1	1	1
16
	0	1	0	1
17
	0	1	0	0
18
	0	0	1	0
19
	0	0	0	1
20
	0	1	1	0
21
		0	1	1

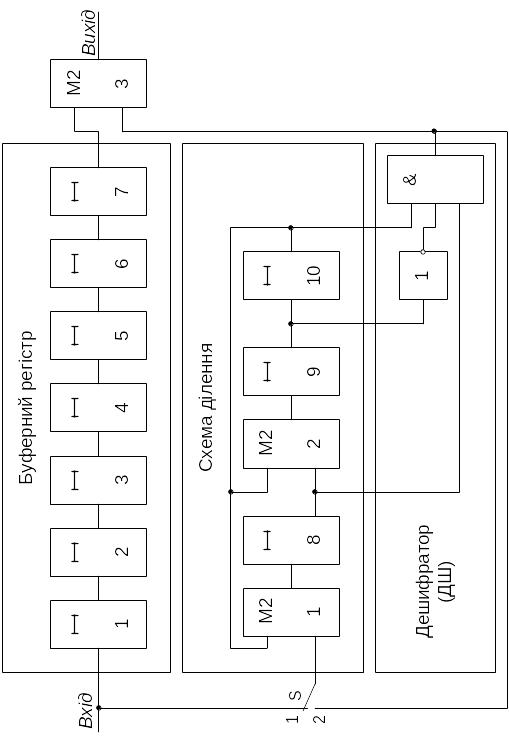
На рис. 3.4 показана схема кодера для вкороченого циклічного коду (9,5) з утворюючим многочленом , виконана на основі схеми обчислення остачі (рис. 3.3). Код має . Крім схеми обчислення остачі від ділення кодер містить два перемикачі: S1 і S2. Перемикач S2 підключає до виходу кодера то вхід кодера, то вихід регістра, чим забезпечується видача або інформаційних символів, або перевірочних. Перемикач S1 розриває зворотний зв'язок при виведенні з регістра перевірочних символів; подачею логічного "0" (лог. "0") забезпечується обнуління регістра перед обчисленням остачі для чергової кодової комбінації.

У табл. 3.6 наведені стани елементів схеми кодера в процесі кодування двох кодових комбінацій з інформаційними частинами 10011 та 01110.

Ділення у стовпчик наборів коефіцієнтів при многочленах інформаційних частин, помножених на , на набір коефіцієнтів при , показує, що остачі від ділення збігаються з перевірочними частинами кодових комбінацій, зазначеними в табл. 3.6:

Декодер циклічного коду, призначений для виявлення помилок, має схему ділення на утворюючий многочлен для обчислення синдрому, дешифратор нульового синдрому та буферний регістр для зберігання прийнятої кодової комбінації на час виконання операції ділення. Якщо синдром буде нульовим, то інформаційна частина кодової комбінації видається з кодера споживачеві, у противному випадку виробляється сигнал "Стирання", що зазвичай забороняє видачу комбінації споживачеві й формує команду для запиту по зворотному каналу повторної передачі даної кодової комбінації.

Існують різні варіанти декодерів для циклічних кодів, що виправляють помилки. Одним з них може бути пристрій синдромного декодування, що використовується у звичайних лінійних кодах. У такій схемі кожному ненульовому синдрому зіставляється вектор помилки (звичайно найбільш імовірний); корекція полягає в поелементному додаванні за модулем 2 цього вектора із прийнятою кодовою комбінацією. Синдром може обчислюватися за допомогою схеми ділення на утворюючий многочлен коду. Зіставлення синдрому вектора помилок здійснюється зазвичай за допомогою комбінаційної схеми, наприклад дешифратора, коли виправляються однократні помилки. Для довгих кодів і високої кратності виправлення помилок така схема досить складна.

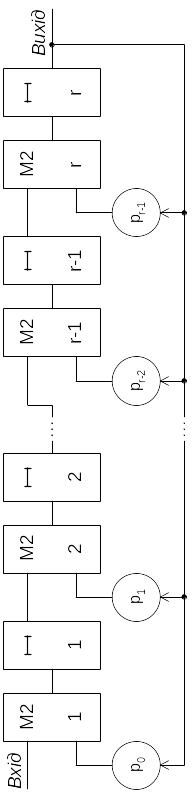
Рис. 3.4. Кодер циклічного коду (9,5)

Описаний вище спосіб побудови декодера, що виправляє помилки, не використовує повною мірою властивості циклічних кодів. Їх урахування дозволяє істотно спростити схему декодера. Принципи такого спрощення розглянемо на прикладі коду (7,4) з утворюючим многочленом , здатного виправляти всі однократні помилки. У табл. 3.7 наведені синдроми для всіх однократних помилок.

Звернемося до табл. 3.5 і випишемо один цикл станів генератора синдрому, побудованого на основі многочлена , починаючи з 10‑го ТІ, при цьому запишемо символи для кожного стану у зворотному порядку, щоб форма запису відповідала формі запису синдромів у табл. 3.7. Отримаємо наступну послідовність станів:

.

Ця послідовність обернена послідовності синдромів, записаних у табл. 3.7. Дана властивість дозволяє для виправлення будь-якої однократної помилки використати дешифратор, налагоджений тільки на один синдром, а для визначення місцезнаходження помилки і її виправлення виконувати синхронно зсуви кодової комбінації в буферному регістрі та зміни станів генератора синдрому доти, доки генератор синдрому не перейде в той стан, на який налагоджений дешифратор, після чого проінвертувати помилковий символ. Зазвичай дешифратор налагоджують на синдром, що відповідає многочлену помилки найбільшого степеня (у даному випадку ). У розглянутому прикладі синдромом є 101.

Таблиця 3.6
Номер ТІ	Вхід	Виходи ЕЗ				Положення перемикача		Вихід	Примітка
		1	2	3	4	S1	S2
	1	0	0	0	0	2	1	1		Інф. симв.		1‑а кодова комбінація
1
	0	1	0	0	1	2	1	0
2
	0	1	1	0	1	2	1	0
3
	1	1	1	1	1	2	1	1
4
	1	0	1	1	1	2	1	1
5
	0	0	0	1	1	1	2	1		Перев. симв.
6
	0	0	0	0	1	1	2	1
7
	0	0	0	0	0	1	2	0
8
	0	0	0	0	0	1	2	0
9
	0	0	0	0	0	2	1	0		Інф. симв.		2‑а кодова комбінація
10
	1	0	0	0	0	2	1	1
11
	1	1	0	0	1	2	1	1
12
	1	0	1	0	0	2	1	1
13
	0	1	0	1	1	2	1	0
14
	0	1	1	0	0	1	2	0		Перев. симв.
15
	0	0	1	1	0	1	2	0
16
	0	0	0	1	1	1	2	1
17
	0	0	0	0	1	1	2	1
18
		0	0	0	0

Таблиця 3.7
Многочлен помилок	Вектор помилок	Синдром

Один з варіантів декодера зображений на рис. 3.5. Декодер складається з буферного регістра, схеми ділення на , дешифратора набору 101, суматора за модулем 2 (номер 3 на схемі), призначеного для інвертування помилкового символу, і перемикача S.

У табл. 3.8 представлені стани елементів схеми декодера в процесі декодування комбінацій 1100001 й 1101101, що будуть отримані з кодової комбінації 1101001 розглянутого коду при спотворенні в ній 4‑го й 5‑го символів відповідно. Прочерки в табл. 3.8 означають, що стани виходів елементів на даних позиціях байдужі.

Схема ділення на виконує дві функції. Під час надходження в кодер і запису кодової комбінації в буферний регістр схема ділення обчислює остачу – синдром (тактові імпульси з 1‑го по 7‑й і з 15‑го по 21‑й), а під час виведення кодової комбінації з буферного регістра схема ділення працює як генератор синдрому до переходу в стан 101; після цього стану комірки схеми ділення за рахунок зворотного зв'язку з дешифратора переходять у нульовий стан. Як випливає з табл. 3.8, між надходженням суміжних кодових комбінацій декодер затрачає тактових імпульсів на виправлення помилки. Якщо кодові комбінації надходять неперервно одна за другою, без часових проміжків, то робота даної схеми можлива лише при збільшенні не менше, ніж у разів частоти надходження тактових імпульсів на час виведення кодової комбінації з буферного регістра й корекції помилки.

Можна побудувати схему декодера, у якій збільшення частоти тактових імпульсів не потрібно. Для цього, наприклад, можна використати в декодері дві схеми ділення. Одна з них виконує тільки обчислення остачі від ділення, після чого ця остача переписується в другу схему ділення, що постійно працює в автономному режимі як генератор синдрому. Введення чергової кодової комбінації в буферний регістр суміщується з виведенням з нього й корекцією попередньої кодової комбінації.

За описаним принципом можна будувати схеми декодування для виправлення помилок більш високої кратності.

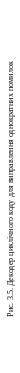
Таблиця 3.8
Номер ТІ	Вхід	Виходи ЕЗ										Вихід ДШ	Положення S	Вихід
		1	2	3	4	5	6	7	8	9	10
	1	-	-	-	-	-	-	-	0	0	0	-	1	-
1
	1	1	-	-	-	-	-	-	1	0	0	-	1	-
2
	0	1	1	-	-	-	-	-	1	1	0	-	1	-
3
	0	0	1	1	-	-	-	-	0	1	1	-	1	-
4
	0	0	0	1	1	-	-	-	1	1	1	-	1	-
5
	0	0	0	0	1	1	-	-	1	0	1	-	1	-
6
	1	0	0	0	0	1	1	-	1	0	0	-	1	-
7
	-	1	0	0	0	0	1	1	1	1	0	0	2	1
8
	-	-	1	0	0	0	0	1	0	1	1	0	2	1
9
	-	-	-	1	0	0	0	0	1	1	1	0	2	0
10
	-	-	-	-	1	0	0	0	1	0	1	1	2	1
11
	-	-	-	-	-	1	0	0	0	0	0	0	2	0
12
	-	-	-	-	-	-	1	0	0	0	0	0	2	0
13
	-	-	-	-	-	-	-	1	0	0	0	0	2	1
14
	1	-	-	-	-	-	-	-	0	0	0	-	1	-
15
	1	1	-	-	-	-	-	-	1	0	0	-	1	-
16
	0	1	1	-	-	-	-	-	1	1	0	-	1	-
17
	1	0	1	1	-	-	-	-	0	1	1	-	1	-
18
	1	1	0	1	1	-	-	-	0	1	1	-	1	-
19
	0	1	1	0	1	1	-	-	0	1	1	-	1	-
20
	1	0	1	1	0	1	1	-	1	1	1	-	1	-
21
	-	1	0	1	1	0	1	1	0	0	1	0	2	1
22
	-	-	1	0	1	1	0	1	1	1	0	0	2	1
23
	-	-	-	1	0	1	1	0	0	1	1	0	2	0
24
	-	-	-	-	1	0	1	1	1	1	1	0	2	1
25
	-	-	-	-	-	1	0	1	1	0	1	1	2	0
26
	-	-	-	-	-	-	1	0	0	0	0	0	2	0
27
	-	-	-	-	-	-	-	1	0	0	0	0	2	1
28
										0	0	0