Короткое замыкание фазы нагрузки

8. Подключить к генератору соединенную звездой симметричную комплексную нагрузку Z_A, Z_B,Z_C без нейтрального провода. Закоротить перемычкой нагрузку Z_A. Провести измерения и записать результаты в таблицу 1.

Обрыв линейного провода

9. Подключить к генератору соединенную звездой симметричную комплексную нагрузку Z _A Z _B Z _C без нейтрального провода. Отключить линейный провод фазы А. Провести измерения и записать результаты в таблицу 11.

Исследование соединения звезда-треугольник

Схема измерений для соединения звезда-треугольник показана на рис. 11 Токи в фазах нагрузки обозначены I _AB I _BC I _CA .Для измерения линейных токов используется измерительное сопротивление R_u =10 Ом.

10. Подключить к трехфазному генератору соединенную треугольником симметричную комплексную нагрузку Z _AB Z_BC Z _CA. Мультиметром измерить линейные напряжения, линейные токи и напряжения на всех элементах нагрузки. Результаты измерений записать в таблицу 2.

Рис. 11

Таблица 2

Соединение звезда-треугольник

Домашнее задание

1. По результатам измерений таблицы 1 для каждого варианта нагрузок построить векторные диаграммы напряжений и токов в трехфазной цепи. Объяснить особенности режимов работы трехпроводной и четырехпроводной цепи при различных нагрузках.

2. Для соединения звезда - звезда рассчитать теоретически при несимметричных нагрузках в четырехпроводной системе ток нейтрали, а в трехпроводной системе напряжение смещения нейтрали. Сравнить расчетные и экспериментальные результаты.

3. Для режима короткого замыкания нагрузки фазы А в трехпроводной системе рассчитать напряжения на элемента фазных нагрузок В и С.

4. Для режима обрыва линейного провода рассчитать напряжения и токи в фазных

нагрузках В и С.

5.По результатам измерений таблицы 2 для соединения звезда - треугольник построить векторные диаграммы напряжений и токов. По диаграммам определить сдвиг фаз между линейными напряжениями и токами в нагрузках. Рассчитать активные и реактивные мощности в нагрузках.

Определить комплексные значения токов в нагрузках I _ab, I_bc, I_са.

Вычислить по формулам линейные токи I_A, I_B, I_C и сравнить с экспериментальными значениями этих токов.

Лабораторная работа №9 Переходные процессы в неразветвленной электрической цепи с источником постоянного напряжения.

Краткое содержание работы.

Исследуется режим заряда конденсатора емкостью С от источника постоянного напряжения через резистор с сопротивлением R, а также режим заряда конденсатора на резистор.

По изображению на экране осциллографа постоянная времени τ цепи заряда и разряда конденсатора, вычисляя сопротивление R резистора.

Исследуется режим заряда конденсатора от источника постоянного напряжения, через резистор и индуктивную катушез резистор и индуктивную катущ000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000ку с индуктивностью L, а также режим разряда конденсатора на резистор и индуктивную катушку.По изображению кривой напряжения на конденсаторе на экране осциллографа экспериментально подбираются параметры R и L, соответствующие периодическому и колебательному разряду конденсатора, а также критическое сопротивление Rкр, при котором процесс в цепи переходит от колебательного к апериодическому. По кривым Uc(t) определяются период собственных колебаний в цепи – Т, логарифмический декремент затухания ln∆ , значения параметров R1 и Rкр.

Основные положения теории.

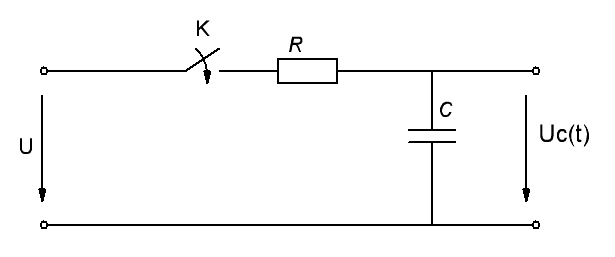
Подключение цепи с последовательным соединением резистивного и емкостного элементов к источнику постоянного напряжения.(рис.1)

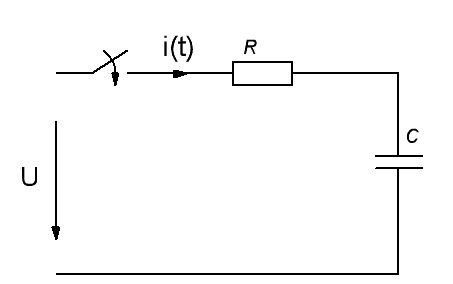
Рис.1

Если t = 0 соответствует моменту подключения источника к цепи и конденсатор емкостью С предварительно не заряжен, то имеем режим заряда конденсатора через резистор. При замкнутом ключе К для такой цепи справедливо уравнение:

или (1)

Решение уравнения имеет вид:

(2)

Постоянная интегрирования А определяется из второго закона коммутации:

Напряжение на конденсаторе изменяется по закону:

(3)

Ток в цепи заряда конденсатора:

(4)

Кривые изменения тока в цепи и напряжения на конденсаторе показаны на рис. 2

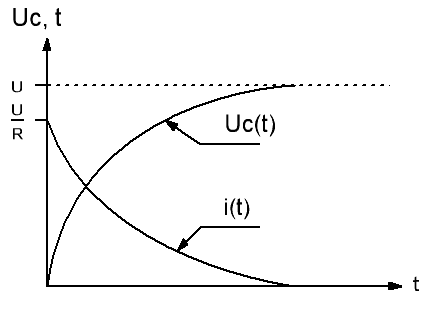
Рис.2

Множитель RC = τ в выражениях (3) и (4) называется постоянной времени цепи. Постоянная времени τ имеет размерность времени и характеризует скорость протекания переходного процесса. При t = τ свободные составляющие уменьшаются по абсолютной величине в e = 2.7 I раз. Графически τ равна величине, подкасательной к экспоненте тока i(t) или напряжения U(t). Переходной процесс можно считать практически завершенным через время t = 3.5 τ , так как к этому времени свободная составляющая напряжения снижается до 3% от своего первоначального значения.

Свободный процесс в цепи с резистивным и емкостным элементами.

Пусть конденсатор с емкостью С, заряженный до напряжения U в момент t = 0 подключается к резистору с сопротивлением R (рис.3)

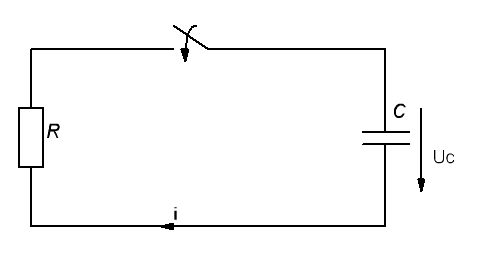
Рис.3

После замыкания ключа для цепи справедливо уравнение

(5)

Решение которого, то есть напряжение на конденсаторе, имеет вид:

(6)

Ток при разряде конденсатора:

(7)

Кривые изменения тока в цепи и напряжения на конденсаторе показаны на рис.4

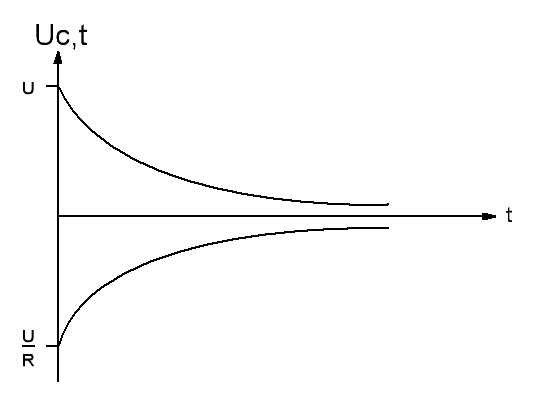
Рис.4

Чем меньше постоянная времени цепи τ = RC , тем быстрее происходит убывание напряжения на конденсаторе и тока в цепи по одному и тому же закону. Поэтому можно также определить по отношения отрезков кривой напряжения на конденсаторе ( или тока в цепи) в соответствующие моменты времени ( рис.5)

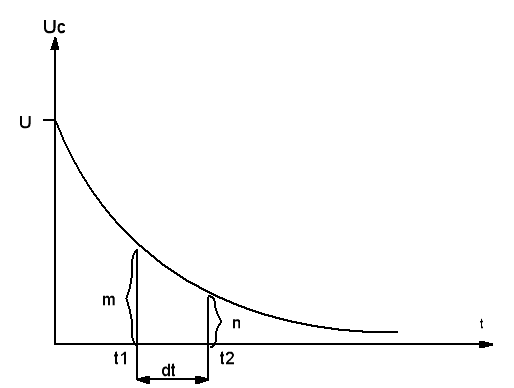
Рис.5

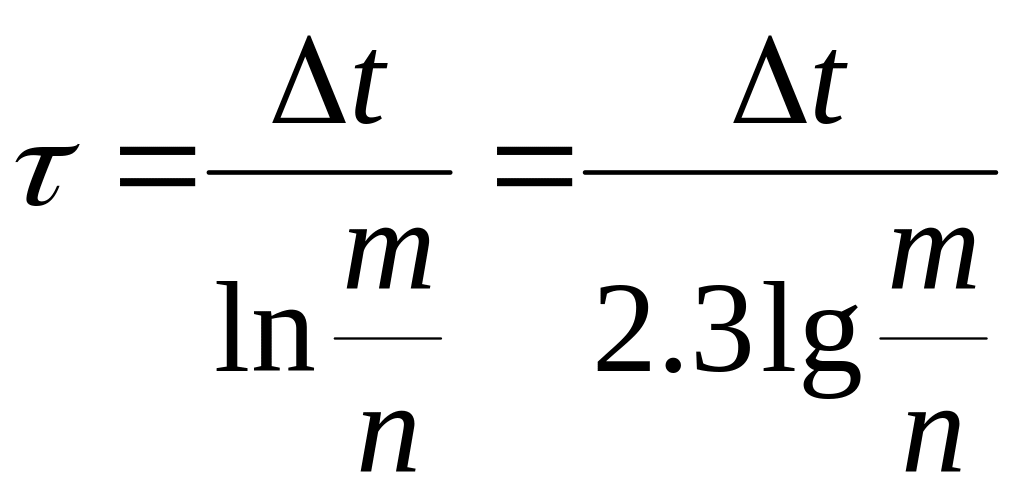(8)

Подключение цепи с последовательным соединением резистивного, индуктивного и емкостного элементов к источнику постоянного напряжения(рис.6).

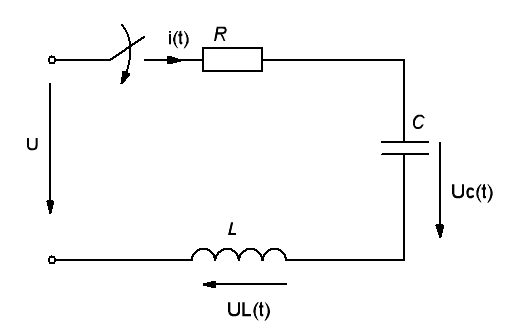
Рис.6

Пусть момент времени t = 0 соответствует моменту включения источника, а напряжение на конденсаторе и ток в цепи до коммутации равны нулю. При этих условиях можно рассматривать режим заряда конденсатор емкостью С через резистор с сопротивлением R индуктивную катушку с индуктивностью L.

После замыкания ключа уравнение равновесия напряжений в цепи будет иметь вид:

(9)

Характеристическое уравнение цепи:

или (10)

Имеет два корня

(11)

Где ,

При решении уравнения (9) возможны три случая ( в зависимости от вида корней характеристического уравнения):

1) (12)

- ( корни отрицательные, вещественные и различные) переходный процесс имеет апериодический характер.

Напряжение на конденсаторе в переходном режиме

(13)

Монотонно возрастает от нуля до U

График изменения Uc(t) показан на рисунке 7

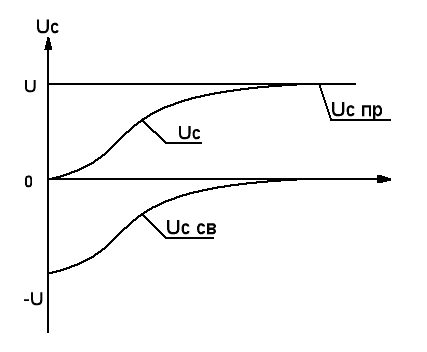
Рис.7

(14)

- ( корни отрицательные, вещественные и равные) предельный случай апериодического процесса.

Напряжение на конденсаторе в переходном режиме:

(15)

Наименьшее резистивное сопротивление, при котором процесс в цепи имеет еще апериодический характер, называется критическим сопротивлением

(16) (17)

- ( корни комплексно-сопряженные) переходной процесс в цепи имеет колебательный характер.

Напряжение на конденсаторе в переходном режиме

(18)

Где - угловая частота колебаний.

Выражение (15) можно привести к виду:

График изменения в колебательном режиме показан на рис.8

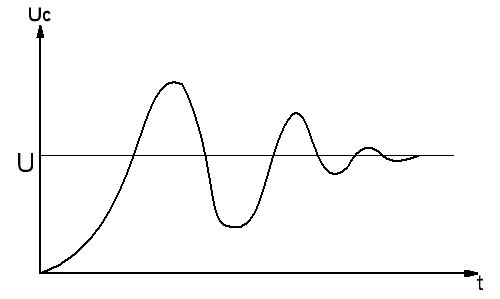
Рис.8

Описание лабораторной установки

На рис 9a изображена рабочая схема для исследования режима заряда конденсатора от источника постоянного напряжения через резистор и разряда его на резистор.

На рис.9а, рис.9б Представлена рабочая схема для исследования режима заряда конденсатора от источника постоянного напряжения через резистор и индуктивную катушку и разряда его на резистор и индуктивную катушку.

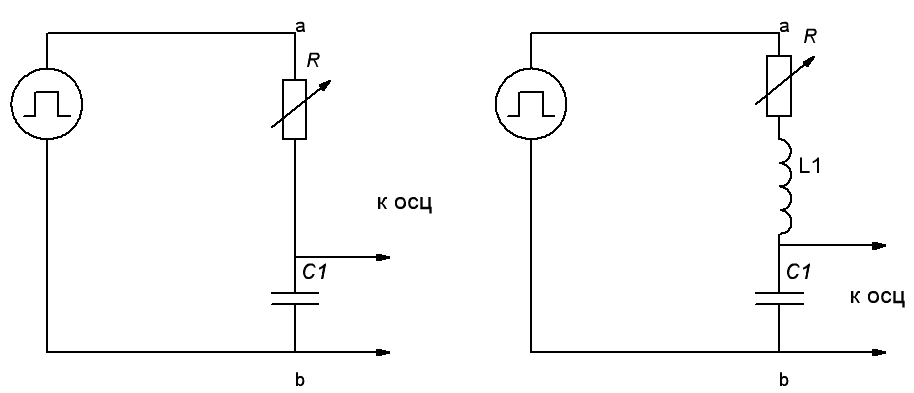
Рис.9а Рис.9б

Однократный заряд и разряд конденсатора не виден на экране осциллографа, так как переходный процесс протекает очень быстро. Поэтому для наблюдения на экране необходимо периодически повторить процесс заряда и разряда конденсатора. Поэтому используется генератор прямоугольных импульсов.

Домашняя подготовка к работе).

4.1 Изучить основные положения теории,

4.2 Ознакомиться с программой эксперимента и методическими указаниями.

4.3 Заготовить протокол отчета:

а)нарисовать рабочую схему цепи для исследования режима заряда конденсатора от источника постоянного напряжения через резистор и разряда конденсатора на резистор ( рис. 8а)

б) записать выражения для тока в цепи i(t), и напряжения на конденсаторе U (t), при его заряде через резистор и нарисовать соответствующие графики;

в) показать способы определения постоянной времени цепи τ. Знать, что называется постоянной времени τ и что она характеризует;

г) нарисовать рабочую схему цепи исследования режима заряда конденсатора от источника постоянного напряжения через резистор и индуктивную катушку и разряда конденсатора на резистор и индуктивную катушку (рис 8б);

д) записать условия апериодического процесса в цепи, предельного случая апериодического процесса и колебательного процесса;

е) записать выражения U (t) для колебательного процесса заряда и разряда конденсатора и нарисовать соответствующие графики;

ж) записать выражения для величин, характеризующих колебательный процесс в цепи;

- период и частота собственных колебаний,

- декремент затухания,

- логарифмический декремент затухания;

з) записать выражения для критического сопротивления цепи через параметры L и C (16)

и) нарисовать кривые изменения напряжения на конденсаторе в случае апериодического процесса заряда и разряда его.

Программа эксперимента

5.1 Собрать цепь для исследования режима заряда конденсатора от источника постоянного напряжения через резистор и разряда конденсатора на резистор.

5.2 Зарисовать кривые U (t), наблюдаемые на экране осциллографа для трех различный сопротивлений R. Значения подбирать из условий:

А) переходной процессы заряда ( разряда) конденсатора не успевает за завершиться за время нахождения ключа;

б) переходной процесс заряда и разряда конденсатора полностью завершается;

в) переходной процесс заряда и разряда конденсатора практически отсутствует (R→0, τ=0).

5.3 По осциллограмме U (t) для условий 5.2 б определить постоянную времени цепи заряда и разряда конденсатора по отношению отрезков кривой напряжения U (t) в соответствующие моменте времени (8);

5.4 По найденной постоянной времени τ рассчитать величину в соответствующего сопротивления резистора R.

5.5 При полученном в п 5.4 значения сопротивления R по формуле 3 рассчитать зависимость U (t) при заряде конденсатора, использую программу П1 и полагая C=68нФ, U=2В.

Полученную кривую сравнить с осциллограммой Uc(t).

…	мкс	0	50	100	150	200	250	300	350	400	450	500
	В

5.6 Собрать цепь для исследования режима заряда конденсатора от источника постоянного напряжения через резистор и индуктивную катушку, а также заряда конденсатора на резистор и индуктивную катушку. ( рис 12в)

5.7 Изменяя величину R установить колебательный процесс, наблюдать изменение напряжения на конденсаторе и зарисовать его.

5.8 По осциллограмме Uc(t) определить период To и частоту собственных колебаний цепи, а также декремент затухания ∆ и логарифмический декремент затухания ln∆

Методические указания

6.1 Длительность развертки осциллографа выбрать так, чтобы на экране был четко виден весь цикл заряда и разряда конденсатора при возможно большем масштабе времени

6.2 Осциллограммы в пункте 5.2 программы эксперимента зарисовать при одинаковом усилении по вертикали.

6.3 Переходной процесс в цепи заряда и разряда конденсатора через резистор полностью завершается через время t =3.5τ, а длительность переходного процесса на экране осциллографа – 500 мкс. Таким образом полностью завершенный переходной процесс возможно наблюдать,

6.4 Период собственных колебаний цепи To. Рекомендуется определять по длительности трех периодов собственных колебаний.

6.5 Декремент затухания определить дважды:

а) как отношение двух соседних положительных амплитуд - ∆1

б) как отношения двух соседних отрицательных амплитуд - , ∆2

Контрольные вопросы к зачету.

8.1 Чему будет равен ток в цепи с последовательным соединением конденсатора емкостью 1мкФ и резистора сопротивлением 1 кОм, подключенной к источнику постоянного напряжения U=10 В, через 1 секунду после подключения?

8.2 Могут ли напряжения на конденсаторе и ток через конденсатор изменяться скачком? Если не могут, то почему?

8.3 Конденсатор емкостью С разряжается на резистор с сопротивлением R=2 кОм и индуктивную катушку с индуктивностью L=36 мкГ. Какова должна быть наименьшая емкость конденсатора, чтобы его разряд на катушку имел апериодический характер?

8.4 Конденсатор емкостью С разряжается на резистор с сопротивлением R=2 кОм и индуктивную катушку с индуктивностью L=36 мкГ. Какова должна быть наименьшая емкость конденсатора, чтобы его разряд на катушку имел колебательный характер?

8.5 По кривой колебательного разряда конденсатора емкостью С= 317 пФ на

RL – цепь определено, что через два периода, равные 2Т= 1мкс, амплитуда напряжения на емкости уменьшилась в е раз. Чему равно R?

8.6 До подключения цепи к источнику постоянного напряжения конденсатор не был заряжен. Определить емкость С конденсатора из условия, что через время t=20 мс после включения ключа К напряжение на конденсаторе при его заряде через резистор с сопротивлением R=3.2 мОм достигает значения U=20 В.