Лабораторная работа №8 Исследование трехфазных электрических цепей

Цель работы: исследование режимов работы трехфазных цепей переменного тока при различных способах соединения симметричных и несимметричных нагрузок. Построение векторных диаграмм токов и напряжений в трехфазных цепях.

Краткие теоретические сведения.

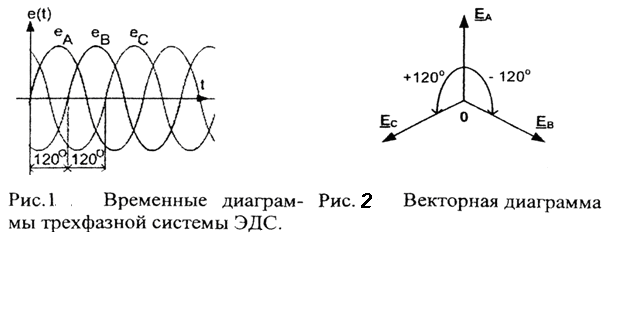
Трехфазные цепи переменного тока являются основным источником электрической энергии в электрических сетях промышленного и коммунального назначения. Трехфазная ЭДС вырабатывается в трехфазных синхронных генераторах и представляется три ЭДС с равной амплитудой и фазовым сдвигом:

На рис. 1 показаны временные диаграммы трехфазных ЭДС. На рис. 2 показана векторная диаграмма комплексных действующих ЭДС в трехфазной цепи.

Применяют несколько способов соединения трехфазного источника ЭДС с нагрузками.

Соединение источника и нагрузки по схеме «звезда – звезда»

Принципиальная схема трехфазной цепи (без нулевого провода ) у которой источник и нагрузка соединены в звезду (рис.3):

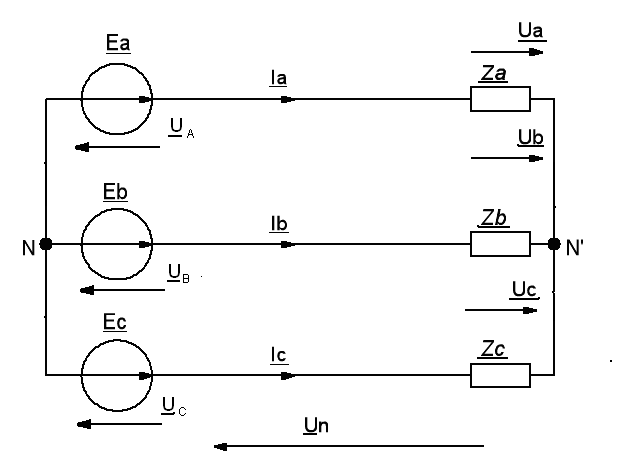
Рис. 3

На схеме U_ФА , U_ФВ , _UФС - комплексы фазных напряжений источников; _UА U_В U_С - комплексы фазных напряжений, - комплекс напряжения смещения нейтрали; Z_A Z_B Z_C комплексы сопротивлений нагрузки.

В симметричном трехфазном источнике три фазных напряжения U_ФА, U_ФВ, U_ФС (напряжения между проводами линии и нейтральной точкой источника N) имеют одинаковые действующие значения и смещены друг относительно друга по фазе . Поэтому их можно представить в виде

U_ФВ = a² U_ФА ; U_ФС = a² U_ФВ = aU_ФА

Где а - фазный множитель

Линейные напряжения (напряжения между линиями)

Модули фазных и линейных напряжений

Связаны при соединении трехфазного источника звездой соотношением:

Топографическая диаграмма напряжения симметричного трехфазного источника:

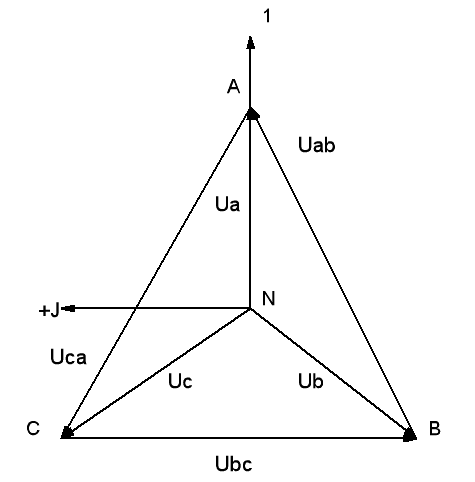Рис. 4

При несимметричной нагрузке токи в ней могут быть определены при помощи законов Кирхгофа

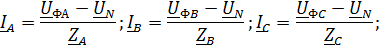Так как сумма этих трех токов должна быть равна нулю, то при получим

Величина (напряжение между точками N и N') называется смещением нейтрали.

Топографическая диаграмма напряжений смещения симметричной трехфазной системы с несимметричной нагрузкой:

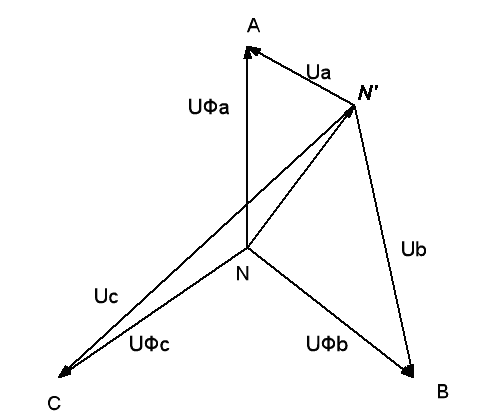
Рис. 5

При напряжение смещения нейтрали равно нулю .

Принципиальная схема трехфазной цепи с нулевым проводом:

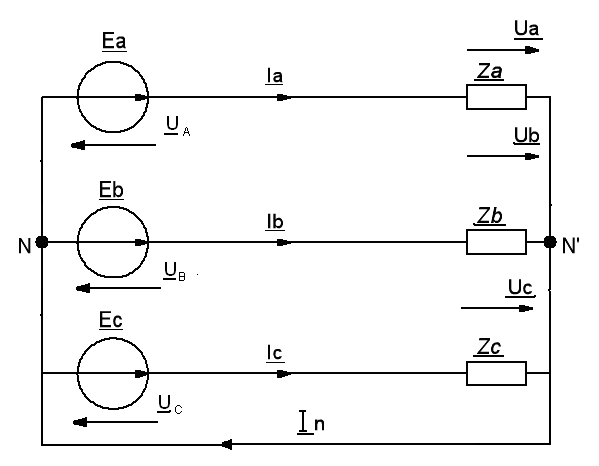
Рис. 6

Для схемы с нулевым проводом как при симметричной нагрузке так и при несимметричной нагрузке напряжение смещения нейтрали а фазные напряжения нагрузки равны фазным напряжениям источника, т.е. U_ФА = U_A; U_ФВ = U_B; U_ФС = U_C

Соединение источника и нагрузки по схеме «звезда – треугольник»

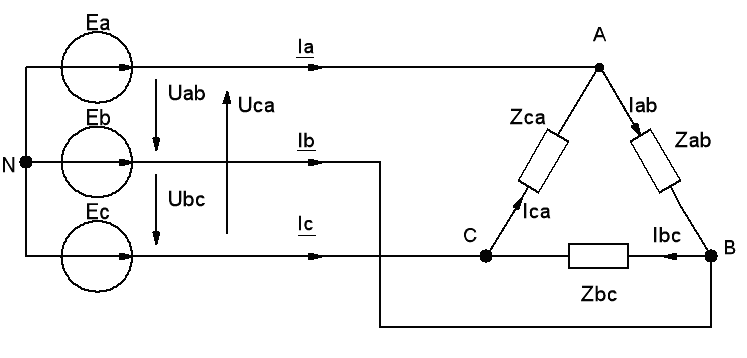
Рис. 7

В этой цепи сопротивления нагрузки находятся под линейным напряжением. Поэтому при любой нагрузке (симметричной и несимметричной) токи в ней могут быть определены из закона Ома.

Линейные токи (токи в проводах линии определяются из первого закона Кирхгофа)

Модули фазных и линейных токов

При соединении симметричной нагрузки треугольником связаны отношением

Мощность трехфазной цепи

Активная мощность трехфазной цепи равна сумме мощностей отдельных фаз

Аналогично реактивная мощность трехфазной цепи равна алгебраической сумме реактивных мощностей отдельных фаз

Поэтому полная мощность или кажущаяся мощность трехфазной цепи может быть определена как

И коэффициент мощности

Независимые от схемы соединения нагрузки (звезда или треугольник), активная мощность симметричной трехфазной цепи, выраженная через линейные токи и линейные напряжения, определяется формулой

Аналогично реактивная мощность симметричной трехфазной цепи

Активная мощность в трехфазной трехпроводной цепи измеряется двумя ваттметрами. При этом возможны три схемы включения ваттметров. Вот одна из них:

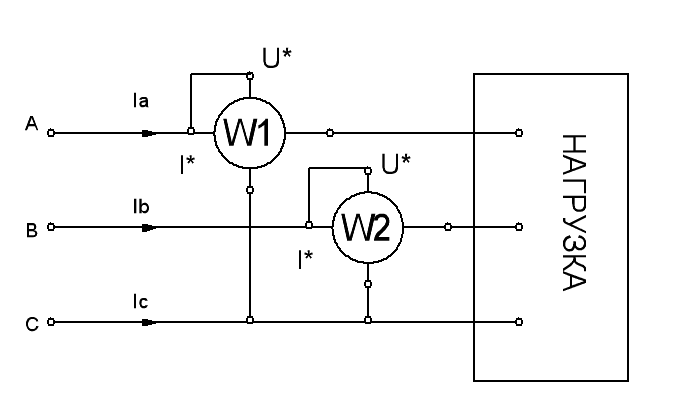
Рис. 8

Активная мощность цепи равна алгебраической сумме показаний отдельных ваттметров т.е.

Симметричные составляющие несимметричных трехфазных напряжений и токов.

Любую систему из трех несимметричных напряжений (или токов ) можно представить как сумму:

1. Систему трех симметричных напряжений с таким же порядком чередования фаз, как и в рассматриваемой несимметричной системе («основная» система или система «прямой последовательности»):

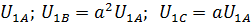
2. Системы трех симметричных напряжений с противоположным порядком чередования фаз («дополнительная система» или система «обратной последовательности»):

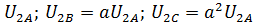
3. Системы трех одинаковых, совпадающих по фазе напряжений(“одинаковофазная система» или система «нулевой последовательности»)

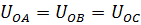
Симметричные составляющие напряжений

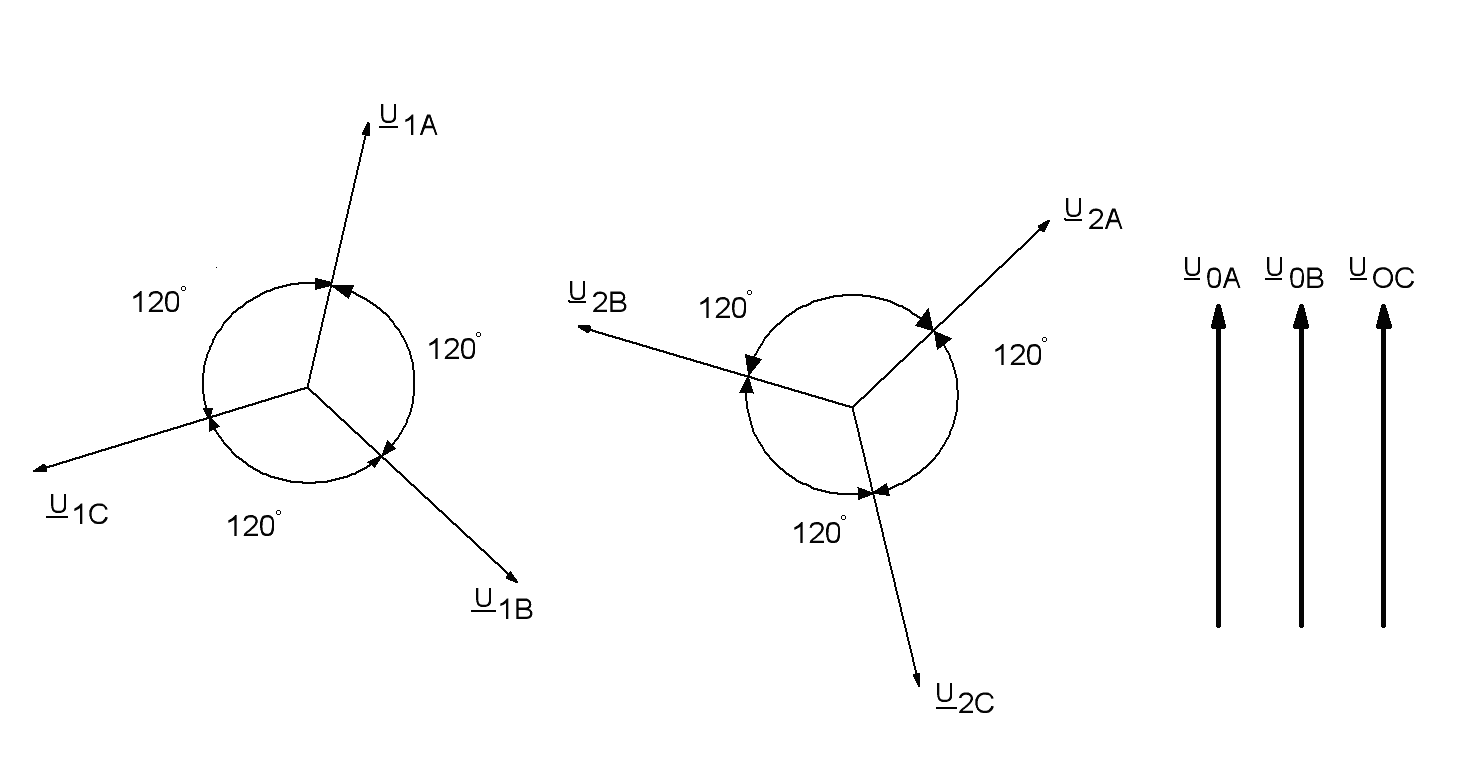
Рис. 9

Таким образом принимают

Учитывая что

получим

Решим эти выражения относительно трех составляющих

При помощи этих уравнений симметричные составляющие легко вычислить или определить графическим построением . после этого токи можно вычислить отдельно для каждой из трех симметричных составляющих теми же методами, что и в случае симметричной систем напряжений. Действительные токи получаются путем сложения трех симметричных составляющих.