Лабораторные работы по оптике

Глава 3. Взаимодействие света с веществом квантовая природа света

3.1. Изучение закона бугера-ламберта

ЦЕЛЬ РАБОТЫ

Изучение явления поглощения (абсорбции) света веществом и экспериментальное подтверждение выполнения закона Бугера-Ламберта.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Электромагнитная волна при прохождении через среду ослабляется вследствие поглощения и рассеяния.

Поглощение света  это явление уменьшения энергии световой волны при ее распространении в веществе, происходящее вследствие преобразования энергии волны во внутреннюю энергию вещества. Поглощение света может вызывать нагревание вещества, возбуждение и ионизацию атомов или молекул, фотохимические реакции и другие процессы в веществе.

Рассеяние света  явление преобразования света веществом, сопровождающееся изменением направления распространения света и проявляющееся как несобственное свечение вещества, обусловленное вынужденными колебаниями электронов в атомах рассеивающей среды под действием падающего света. Оно происходит в оптически неоднородной среде, показатель преломления которой изменяется скачками от точки к точке среды вследствие флуктуаций плотности среды (молекулярное рассеяние), либо за счет присутствия в среде инородных малых частиц (мутная среда - дым, туман, эмульсии и др.). Рассеяние света в мутных средах на частицах, размеры которых малы по сравнению с длиной волны, называется явлением Тиндаля. Теория молекулярного рассеяния разреженными газами была развита польским физиком М. Смолуховским; а жидкостями  А. Эйнштейном.

Закон ослабле­ния света был экспериментально установлен французским ученым П. Бугером и впоследствии теоретически выведен немецким ученым И.Ламбертом. Пусть пучок параллельных лучей, начальная интенсивность которых при х =0 равна I₀ распространяются в поглощающей среде (рис. 1).

П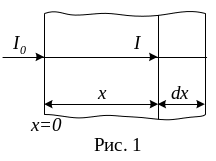 ройдя в среде путь х, свет за счет поглощения и рассеяния ослабляется и его интенсивность I становится меньше первоначальной I₀. Выделим участок среды толщиной dх. Интенсивность света, прошедшего путь х + dх, равная I  dI, будет меньше, чем I, то есть dI  0 (ослабление). Величина  dI представляет собой лучистый поток, поглощенный и рассеянный на участке dх и она, очевидно, пропорциональна толщине этого участка dх и интенсивности падающего (на этот участок) света I, т.е.

. (1)

Коэффициент пропорциональности  называется коэффициентом ослабления света.

Разделив переменные и интегрируя выражение (1) в пределах от I₀ до I, получим

, , ;

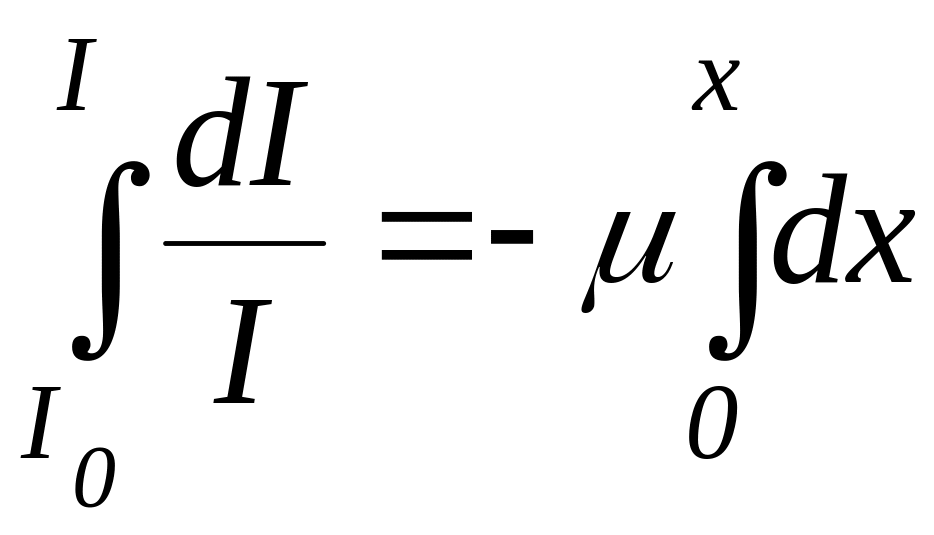. (2)

П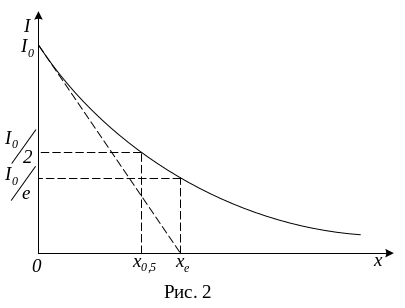 олученное выражение носит название закона Бугера-Ламберта. На рис. 2 показан график (экспонента) этой зависимости.

Коэффициент ослабления  складывается из коэффи­циента поглощения и коэффициента рассеяния:

. (3)

Первый из них ( ) характеризует долю поглощенной энергии ( ) на единице пути (dх = 1), перешедшей в другие формы энергии в основном в тепловую. Второй ( ) аналогичным образом характеризует долю энергии первичного пучка, унесенную рассеянным светом во все стороны.

Коэффициент ослабления  зависит только от длины волны света, химической природы и состояния вещества и не зависит от интенсивности света. С.И. Вавилов установил, что закон Бугера-Ламберта выполняется в довольно широких пределах изменения интенсивности света. Зависимость коэффициента µ от длины волны, характеризующая спектр поглощения света в этой среде, связана с явлением резонанса при вынужденных колебаниях электронов в атомах и атомов в молекулах диэлектрика. Он имеет размерность обрат­ной длины (м^-1) и называется линейным коэффициентом ослабления светового потока. Его физический смысл легко устано­вить, преобразовав уравнение (1) следующим образом:

. (4)

Если толщина слоя , отношение . То из (4) имеем:

. (5)

Таким образом, коэффициент ослабления численно равен обратной величине толщины слоя вещества, по прохождении кото­рого интенсивность света уменьшается в "е" раз (е = 2,7182.. - основание натуральных логарифмов). На рис.2 показано также, что характеризует расстояние, на котором свет поглотился бы полностью, если бы абсолютное поглощение (dI) не убывало по мере сниже­ния интенсивности проходящего потока.

На рис. 2 (в логарифмических координатах) отмечена еще так называемая толщина слоя половинного ослабления х_0,5, определяемая из условия: , ;

. (6)

Часто пользуются массовым коэффициентом ослабления _ лучей, так как коэффициент ослабления обычно пропорционален плотности .

; . (7)

В этом случае закон Бугера-Ламберта принимает вид:

. (8)

Произведение х при этом характеризует массу поглощающего вещества, приходящуюся на единицу площади прошедшего пучка ( ).

При поглощении света веществами, растворенными в практически не поглощающем растворителе (например, в чистой воде), коэффициент ослабления часто пропорционален концентрации растворенного вещества С:

. (9)

Эта зависимость была получена на опыте немецким ученым А. Бером и называется правилом Бера.

Для таких растворов закон поглощения (закон Бугера-Ламберта-Бера) принимает вид:

, (10)

где  новый коэффициент ослабления (поглощения), не зависящий от концентрации и характерный для молекулы поглощающего вещества. Следует отметить, что в реальных газах и растворах закон Бугера-Ламберта-Бера выполняется далеко не всегда.

Измеряя поглощение света слоем такого раствора (толщиной х) и зная коэффициент ослабления , можно отсюда найти концентрацию исследуемого раствора:

. (11)

При достаточно больших значениях интенсивности света закон Бугера-Ламберта нарушается: показатель поглощения диэлектрической среды начинает зависеть от интенсивности света, уменьшаясь с ее ростом, что противоречит классической физике. Ответ дает квантовая теория: при поглощении света часть молекул среды переходит в возбужденное состояние. Такие молекулы не могут участвовать в дальнейшем поглощении света до тех пор, пока они не вернутся, растратив всю свою энергию, в невозбужденное (стационарное) состояние. Закон Бугера-Ламберта выполняется лишь в том случае, если доля возбужденных молекул незначительна.

Можно осуществить такое неравновесное состояние среды, при котором доля возбужденных молекул будет столь велика, что показатель поглощения * становится отрицательным. Это явление, соответствующее отрицательности *, используется в квантовых генераторах радиоволн и света (лазерах).Тогда такая среда называется активной и происходит усиление света по закону Бугера-Ламберта-Фабриканта

. (12)

Закон Бугера-Ламберта в принципе применим для всего диапазона электромагнитных из­лучений видимого света, инфракрасных и ультрафиолетовых лучей, радиоволн, рентгеновских и гамма - лучей. Однако при его практическом применении следует учесть, что при некото­рых условиях он может иметь лишь приближенный характер. Коэффициент ослабления зависит от длины волны света и закон Бугера-Ламберта справедлив для монохроматического света, если частота света далека от резонанса с частотами колебаний электрических зарядов в атомах вещества.

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Экспериментальная установка, представленная на рис.3а, состоит из лампы накаливания мощностью 5 Вт, питаемой стабилизированным напряжением 0 - 12 В от источника питания ВИП-О10. Свет проходит через конденсорную линзу и попадает на дымчатые светофильтры (10 шт.). Bсe 10 светофильтров совершенно одинаковы, имеют толщину 7 мм каждый, и закреплены так, чтобы их легко можно было вынимать и помещать на пути лучей, падающих на фотоэлемент "ФЭ". Ток, вырабатываемый фотоэлементом, измеряется цифровым микроамперметром с ценой деления 10^-8 А. Это значит, что, например, показание прибора I₀ = 5000 нужно рассматривать как i = 50 мкА. Так как сила тока через фотоэлемент пропорциональна интенсивности света и конечным интересующим нас результатом эксперимента является натуральный логарифм относительной интенсивности, поэтому, с целью удобства расчетов, будем снимать четырехзначные значения со шкалы прибора и принимать их за усл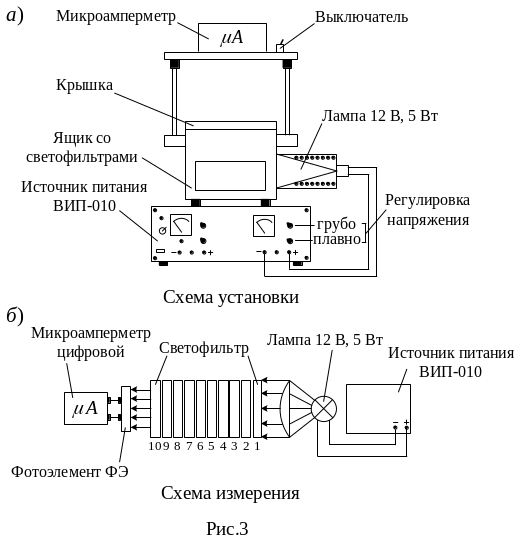 овные значения интенсивности света (I₀ = 5000, 4000, 3000 и т.д.)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Откройте крышку ящика светофильтров и рукой поверните на 90 к себе все 10 светофильтров, убрав их с пути световых лучей, падающих на фотоэлемент. Внимание! Прикасаться можно только к оправам светофильтров, чтобы не запачкать их оптические поверхности. Плотно закройте на крючок крышку ящика (рис.3а).

2. Подключите шнуры питания установки и источника питания ВИП-010 к сети 220 В. Шнур питания лампочки (12 В; 5 Вт) должен быть подключен к клеммам "+" и "-" одного из выходов источника ВИП-010; полярность подключения для лампы роли не играет. Регулятором напряжения "грубо" и "плавно" поверните влево до упора (против часовой стрелки). Переключатель рода работы ВИП-010 поставьте в положение "одиночн." (кнопка отжата).

3. Включите тумблеры «сеть» источника ВИП-010 и прибора. При этом на источнике ВИП-010 должен загореться индикатор сети, а шкала микроамперметра должна показать четыре нуля. Регулятором "грубо" источника ВИП-010 в этой работе не пользоваться! Он должен быть установлен на цифру "10" в процессе всей работы. Регулятор «плавно» состоит из двух соосных потенциометров - для макро- и микрорегулирования. Потенциометр макрорегулировки дает возможность регулировать напряжение, подаваемое на лампу, от нуля до 12 В (при цифре "10" регулятора "грубо"), а микрорегулятор (та же ручка) - регулирует в пределах 0,03 - 0,11 В около установленного макрорегулятором значения. Покрутите регулятор "плавно" и ощутите работу двух потенциометров на одной оси.

4. Установите с помощью регулятора "плавно" показание I₀ = 5000 на шкале микроамперметра при плотно закрытой крышке ящика со светофильтрами.

5. Откройте крышку ящика и рукой введите в зону светового пучка светофильтр №1 (рис.3б). Закройте плотно крышку ящика и запишите показания прибора в таблицу.

6. Вводите поочередно 2, 3, 4, ... 10 светофильтры и, плотно закрыв крышку, запишите показания прибора в таблицу.

7. Выведите все светофильтры из зоны действия световых лучей.

8. Установите с помощью регулятора "плавно" показание I₀ = 4000 на микроамперметре и проделайте п.п. 5, 6, 7. Показания прибора занесите в таблицу. Проделайте те же пункты 5, 6, 7 при показаниях I₀ = 3000 и I₀ = 2000 и заполните соответствующие строки таблицы.

Таблица

Количество светофильтров "n" (шт.)	0	1	2	3	4	5	6	7	8	9	10
Толщина слоя вещества, см	0	7	14	21	28	35	42	49	56	63	70
i0 = 50 mА	I0 = 5000
Отношение	1
i0 = 40 mА	I0 = 4000
Отношение	1
i0 = 30 mА	I0 = 3000
Отношение	1
i0 = 20 mА	I0 = 2000
Отношение	1
Среднее значение	1
	0
По закону Бугера-Ламберта		0

9. Вращением регулятора "плавно" влево до упора установите нулевое показание прибора и выключите тумблеры "сеть" на установке и на источнике питания ВИП-010.

10. Для интенсивностей 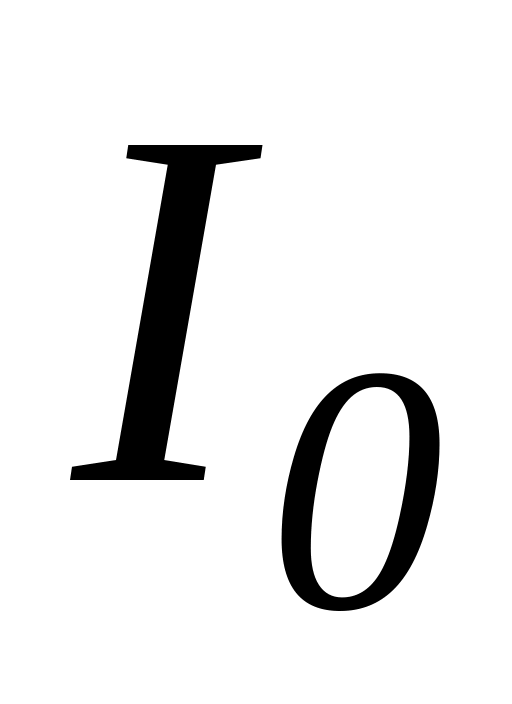, соответствующих значениям 5000, 4000, 3000, 2000, рассчитайте отношения 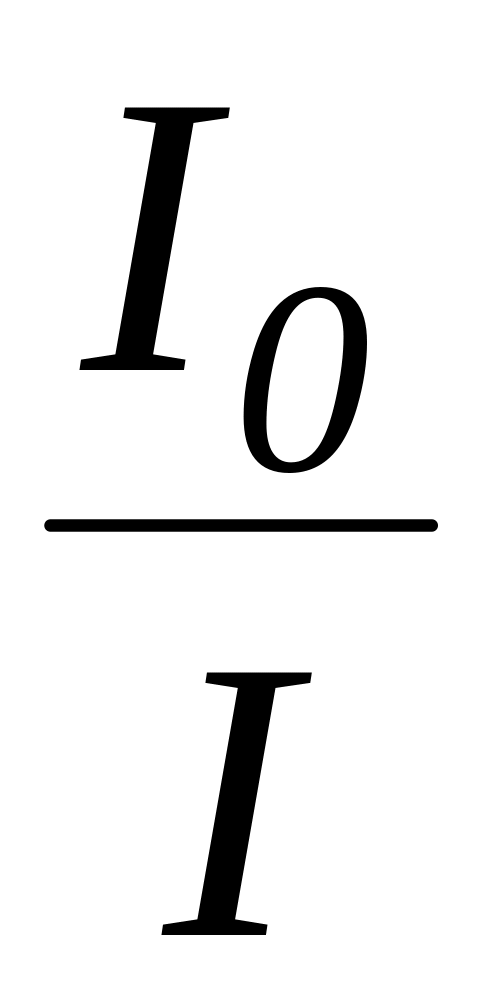при вводе одного, двух, ... десяти светофильтров и заполните таблицу.

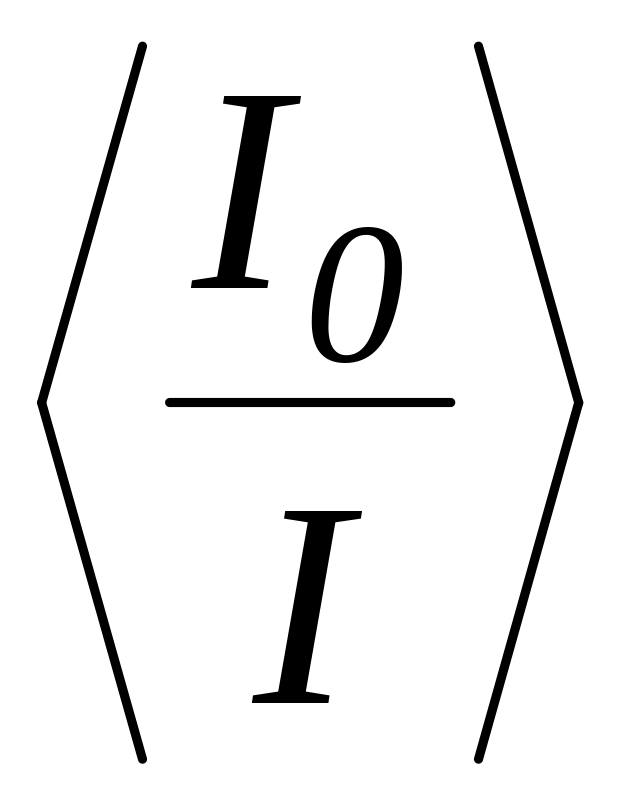11. Найдите средние значения для одного, двух, трех и более (до десяти) светофильтров и заполните строчку средних значений . В следующей строке таблицы запишите натуральные логарифмы этих значений.

12. Конечной целью работы является построение графика закона Бугера-Ламберта и сравнение экспериментальных данных с теоретическими. Такое сравнение удобно проводить, представив график закона в виде прямой линии. Из формулы (4) получим выражение

, (13)

к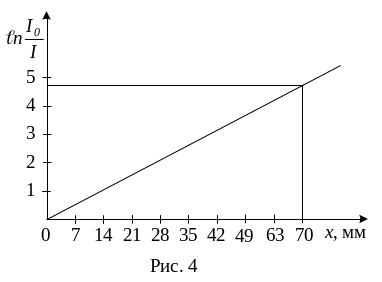 оторое является уравнением прямой линии (в полулогарифмических координатах). Постройте на графике эту прямую, пользуясь исключительно миллиметровой бумагой стандартного формата А4 (размер обычного машинописного листа). По оси абсцисс отложите х (мм). Удобнее, начиная с перекрестка жирных линий миллиметровки, отложить по оси х цифры (через каждые 15 мм) 0, 7, 14, 21, 28, …, 70. Это ничего, что они не кратны числу 15 - нам промежуточные значения не понадобятся. По оси ординат отложите через каждые 5 см цифры 1, 2, 3, 4 - это ось значений (рис. 4).

Для построения теоретической прямой закона Бугера-Ламберта (13) нам достаточно начало координат соединить с одной точкой, например, при х = 70 мм. Коэффициент поглощения применяемых в данной работе светофильтров равен  = 0,0668 мм^-1, следовательно, .

Нанесите на график (рис.4) эту точку с координатами х = 70 мм, и проведите теоретическую прямую закона Бугера-Ламберта, соединив ее с началом координат.

13. Нанесите на график экспериментальные значения 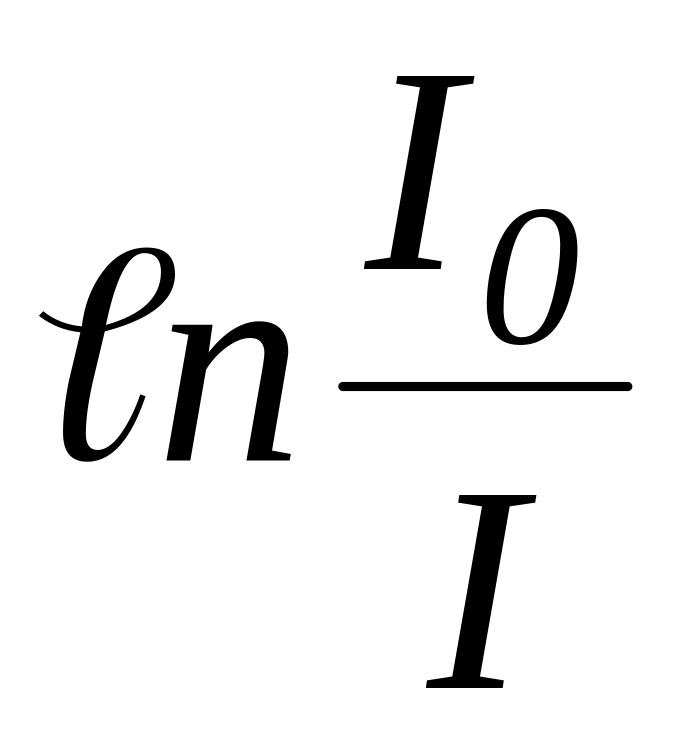из таблицы в виде точек и оцените совпадения теоретических и экспериментальных данных.

14. Для более глубокого анализа полученных результатов их можно обработать известным способом наименьших квадратов. При этом нужно рассчитать и заполнить строку теоретических значений таблицы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Укажите цель данной лабораторной работы.

2. Что происходит с энергией электромагнитной волны при прохождении через различные среды?

3. Объясните механизм поглощения света.

4. Объясните явление рассеяния света.

5. Какие процессы возникают при поглощения света веществом?

6. В каких средах происходит рассеяние света?

7. Сформулируйте явление Тиндаля.

8. Сформулируйте закон Бугера-Ламберта.

9. Выведите формулу (закон) Бугера-Ламберта.

10. Назовите составляющие, которые характеризуют коэффициент ослабления  в законе Бугера-Ламберта.

11. От каких параметров зависит коэффициент ослабления ?

12. Каков физический смысл коэффициента ослабления?

13. Укажите размерность коэффициента ослабления.

14. Выведите условие, определяющее толщину слоя половинного поглощения.

15. Дайте определение массового коэффициента ослабления _.

16. Напишите закон Бугера-Ламберта через массовый коэффициент ослабления _.

17. Сформулируйте правило Бера.

18. Как определить концентрацию раствора, используя закон Бера в законе Бугера-Ламберта?

19. Как изменяется показатель поглощения среды при значительном увеличении интенсивности света?

20. Может ли показатель поглощения принимать отрицательное значение?

21. Опишите работу данной лабораторной установки.

22. Опишите порядок выполнения измерений.

23. Каково количество светофильтров, используемых в установке?

24. Что будет происходить с показаниями цифрового микрометра, если крышку ящика светофильтров закрыть неплотно?

25. Объясните назначение конденсорной линзы в установке.

26. Как изменятся результаты эксперимента, если угол падения лучей на поверхность светофильтра будет отличен от нуля?

27. С какой целью в данной лабораторной работе рассчитывается относительная интенсивность света?

28. Объясните, каким образом экспоненциальная зависимость закона Бугера-Ламберта представлена графически в виде прямой линии.

29. Изменится ли ход экспериментальной кривой в случае, если при выполнении эксперимента изъять некоторые светофильтры?

30. Объясните, почему в данной лабораторной работе используется полулогарифмический масштаб при построении графиков теоретической и экспериментальной кривых.