Катушки индуктивности на переменное напряжение

2. Схему рис.14.1 подключить к источнику регулируемого переменного напряжения (ЛАТРу); не забыть предварительно повернуть рукоятку ЛАТРа против часовой стрелки до упора. С помощью подключенного к зажимам источника вольтметра выставить напряжение на входе схемы в пределах 70...80 В. Переключатель "Период коммутаций" поставить в положение "8Т". С помощью регуляторов "Время/дел." установить требуемый размер изобра­же­­ния, после чего засинхронизировать его (см. приложение 12.2 к лабора­торной работе №12).

3. С помощью регулятора "Начальная фаза" установить заданное (задается преподавателем) значение начальной фазы напряжения. Зарисовать осциллограмму на кальку, указать масштабы по осям. Записать значение напряжения источника.

4. Снять зависимость амплитуды первого броска тока от начальной фазы переменного напряжения (с шагом 10 градусов). Построить кривую указанной зависимости и проанализировать полученные результаты. Рассчитать отношение максимального броска тока к его амплитуде в установившемся режиме (рис. 14.3).

5. Изменяя начальную фазу коммутации регулятором "Начальная фаза", добиться отсутствия в цепи переходного процесса на переменном напряжении. Записать положение регулятора фазы.

6. Снять зависимость амплитуды первого броска тока от величины переменного напряжения при начальной фазе, равной "0" (в пределах от 25 до 80 В). Построить кривую указанной зависимости и проанализировать полученные результаты.

7. Рассчитать заданным преподавателем методом переходный процесс при подключении нелинейной катушки индуктивности к источнику переменного напряжения для величины напряжения и значения его начальной фазы, принятых в п.7 (см. метод. указания). Совместить на одном графике экспериментальную и расчетную кривые, дать их сравнительный анализ.

8. Определить, при каком значении начальной фазы переменного напряжения переходный процесс в цепи будет отсутствовать (см. метод. указания). Сравнить это значение со значением начальной фазы, полученным в п.9.

Примечание. Пункты 9, 10, 12 являются творческими заданиями и выполняются по указанию преподавателя.

Методические указания

К пункту 5.

При пренебрежении потоками рассеяния (используемая в опыте катушка индуктивности выполнена на сердечнике без воздушного зазора) уравнение, описывающее переходный процесс в цепи на рис. 14.1, имеет вид

, (14.1)

где .

Уравнение (14.1) в силу нелинейности характеристики катушки является нелинейным. В этой связи для его решения используют приближенные методы, наибольшее распространение из которых получили метод условной линеаризации, метод кусочно-линейной аппроксимации, метод аналитической аппроксимации и ряд других [1…5,9,10].

Метод условной линеаризации целесообразно применять в случаях, когда падение напряжения на резисторе мало по сравнению с напряжением на катушке. При его использовании нелинейная вебер-амперная характеристика катушки индуктивности заменяется прямой линией, проходящей через начало координат и точку установившегося режима, определяемую током

. (14.2)

Таким образом, решение уравнения (14.1) осуществляется для линейной вебер-амперной зависимости , где . При этом само соотношение (14.1) трансформируется в уравнение

или

, (14.3)

где – эквивалентная постоянная времени.

При решении (14.3) определяется функция , по которой с использованием нелинейной зависимости рассматривается (строится) кривая .

Качественный вид зависимости в электрической цепи с линейной и нелинейной катушками представлен на рис. 14.2.

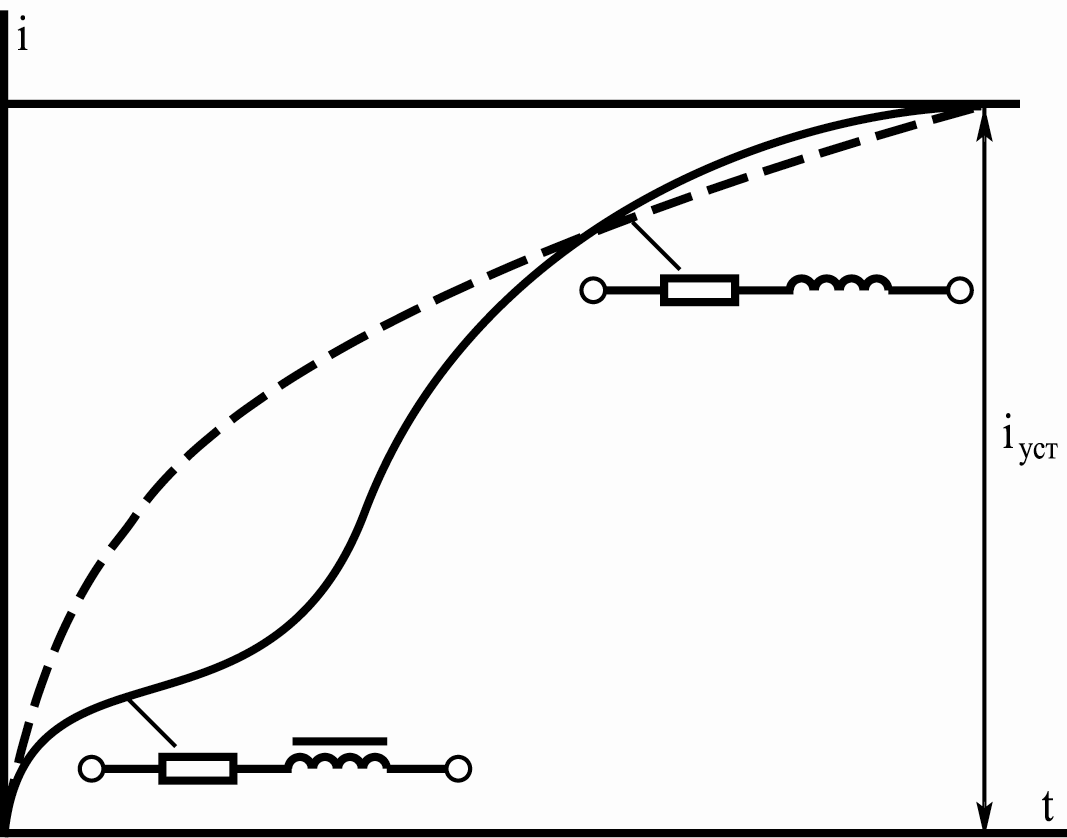
Рис.14.2. Переходные процессы при включении на постоянное напряжение

линейной и нелинейной катушек индуктивности

Метод кусочно-линейной аппроксимации основан на замене характеристики нелинейного элемента ломаной линией. В пределах каждого из прямолинейных участков ломаной переходный процесс описывается линейным дифференциальным уравнением. Таким образом, осуществляется переход от исходного нелинейного уравнения (14.1) к нескольким линейным уравнениям вида

, (14.4)

отличающимся друг от друга только значениями индуктивности для соответствующего к-го отрезка ломаной. При этом величина определяется тангенсом угла, образованного к-м отрезком с осью абсцисс (токов).

Каждое из линейных уравнений (14.4) справедливо для того временного интервала, в течение которого рабочая точка перемещается по соответствующему линеаризованному участку. Временные границы каждого участка (при анализе переходного процесса данным методом их расчет является необходимым этапом) определяются исходя из достижения током своих граничных значений для рассматриваемого прямолинейного отрезка. В соответствии с законом коммутации значения тока в ветви с катушкой индуктивности в эти моменты времени являются начальными значениями для соседних прямолинейных участков, на основании чего определяются постоянные интегрирования.

При расчете переходного процесса в цепи на рис. 14.1 данным методом нелинейную вебер-амперную характеристику следует заменить ломаной с числом прямолинейных участков не менее 3. Первый из них должен проходить через начало системы координат, а последний – через точку зависимости , соответствующую установившемуся режиму (см. (14.2)).

Метод аналитической аппроксимации основан на аппроксимации характеристики нелинейного элемента аналитической функцией, которая должна достаточно точно отображать используемую нелинейную характеристику на участке перемещения рабочей точки и в то же время обеспечивать возможность достаточно простого интегрирования дифференциального уравнения.

Численные значения коэффициентов в выражении аналитической аппроксимации следует определять из условия их соответствия заданной характеристике в точке установившегося режима (см. (14.2)).

Принятое выражение аналитической аппроксимации подставляется в уравнение (14.1) и осуществляется его интегрирование (в том числе с использованием табличных интегралов).

К пунктам 7,8.

Рис.14.3. Типовая кривая тока в цепи с нелинейной катушкой индуктивности при включении на переменное напряжение