Действующее значение тока в каждой из ветвей определяется как

, (11.2)

где – действующее значение к-й гармоники тока.

Аналогично определяется действующее значение напряжения:

, (11.3)

где – действующее значение к-й гармоники напряжения.

Мощность Р определяется выражением

, (11.4)

где – углы сдвига между напряжением и током соответствующих гармоник.

В качестве примера рассмотрим расчет действующих значений входного тока и напряжения на конденсаторе, а также активной мощности в цепи на рис. 11.5, питаемой от источника несинусоидального напряжения;

.

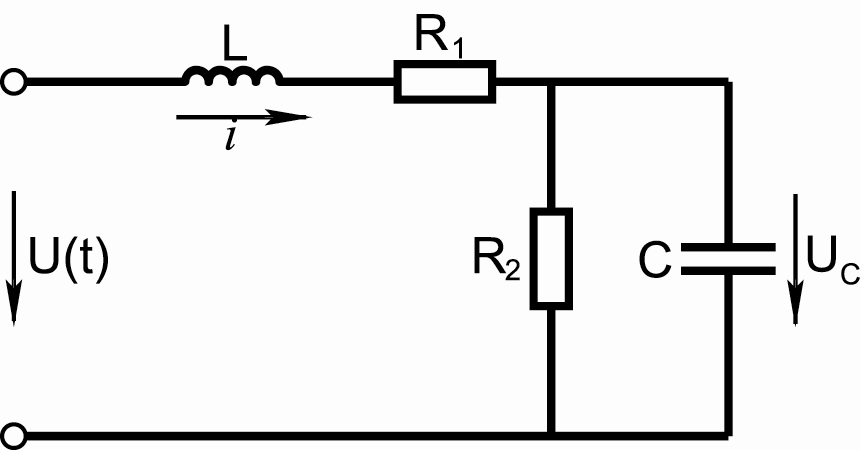Рис. 11.5. К примеру расчета цепи несинусоидального тока

1. В соответствии с методом наложения и с учетом выражений (11.1) реактивных сопротивлений катушки индуктивности и конденсатора для к-й гармоники тока исходную цепь на рис. 11.5 заменим расчетными на рис. 11.6: схемой а – для нулевой гармоники и схемой б – для к-х гармоник.

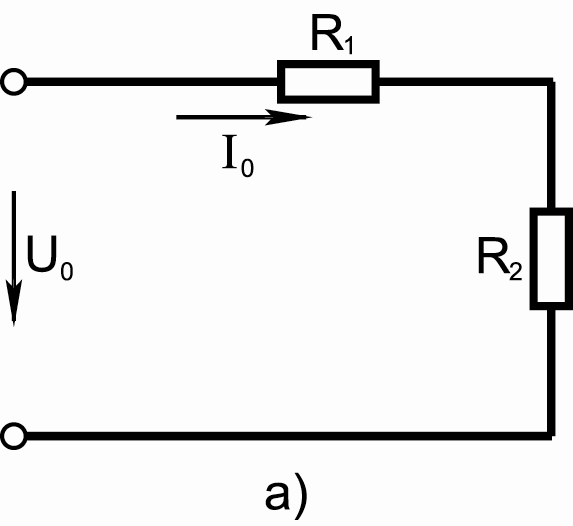
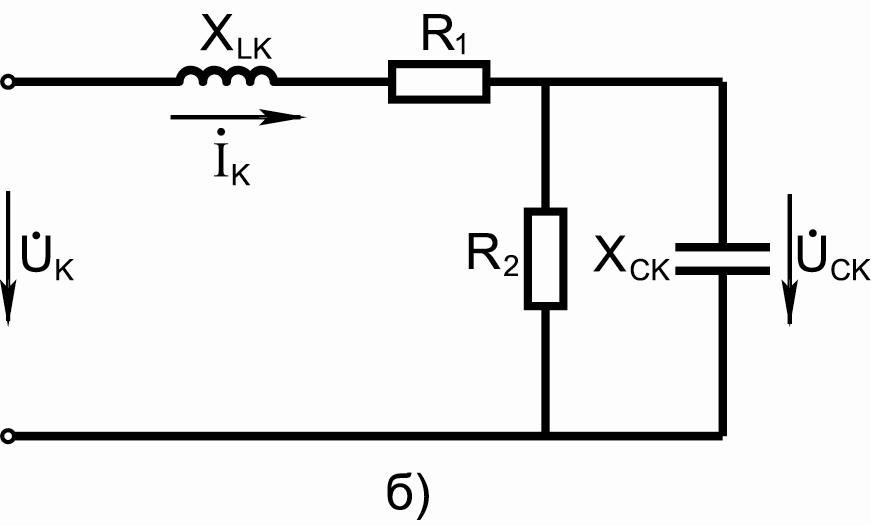
Рис. 11.6. Расчетные схемы замещения для нулевой (а) и к-й (б) гармоник

2. По цепи на рис. 11.6,а определяются постоянные составляющие I и U_C:

; (11.5)

. (11.6)

3. Расчет цепи на рис. 11.6,б для каждой к-й гармоники входного напряжения дает соответствующие гармоники I и U_C:

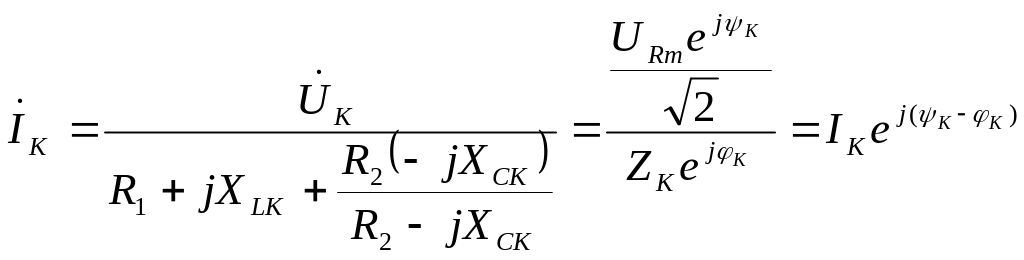; (11.7)

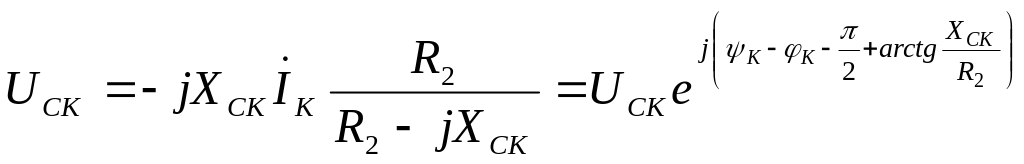, (11.8)

где – действующее значение к-й гармоники входного тока; – действующее значение к-й гармоники напряжения на конденсаторе.

4. Полученные согласно (11.5) – (11.8) модули гармоник тока и напряжения на конденсаторе подставляются соответственно в соотношения (11.2) и (11.3), на основании которых находятся искомые действующие значения I и U_C.

5. Необходимые для расчета активной мощности P источника по (11.4) фазовые сдвиги между к-ми гармониками входного напряжения и тока берутся из (11.7).

К творческому заданию.

Особенность резонанса в линейных цепях при несинусоидальных токах заключается в том, что он может иметь место на первой или на высших гармониках. Это свойство часто используется в различных видах полосовых и режекторных фильтров. Так, например, для последовательной R–L–C – цепи комплексное сопротивление к-й гармоники может быть представлено выражением

, (11.9)

где – комплекс сопротивления цепи для k-й гармоники;

k -1,2,3,... – порядковый номер гармоники;

– угловая частота основной (первой) гармоники;

R,L,C – параметры цепи (считаются независимыми от частоты).

Выражение (11.1) показывает, что резонанс напряжение в цепи может быть только на какой-то одной гармонике, тогда

.

Это приводит к резкому увеличению процентного содержания этой гармоники в общем гармоническом составе несинусоидального тока.

Контрольные вопросы

1. Назовите причины возникновения несинусоидальных токов и напряжений в электрических цепях.

2. Как связано действующее значение несинусоидального тока (напряжения) с амплитудами отдельных гармоник?

3. Чем отличаются идеальные характеристики нелинейных элементов от их реальных характеристик?

4. Как определить активную, реактивную и полную мощности в цепи при несинусоидальном источнике питания?

5. Что такое коэффициент мощности в цепях с несинусоидальным током?

6. Поясните, почему в цепях с несинусоидальным током при работе на активную нагрузку может отличаться от 1.

7. Запишите выражение для коэффициентов формы, искажений, гармоник и амплитуды. Поясните входящие в них величины.

8. Как связаны коэффициенты искажения несинусоидальной функции и ее производной?

9. Постройте резонансную кривую для цепи при последовательном и параллельном соединениях элементов (параметры цепи задает преподаватель).

10. Назовите методы анализа цепей несинусоидального тока.

11. Каково применение несинусоидальных токов и напряжений на практике?

17