Раздел 3. Нелинейные системы автоматического управления

3.1 Примеры учёта нелинейностей в реальных системах автоматического управления. Характеристики нелинейных звеньев

Существует множество систем, процессы в которых принципиально не могут быть описаны линейными диф­ференциальными уравнениями, и при их исследовании необходимо пользоваться нелинейными дифференциальными уравнениями.

Переход к нелинейным дифференциальным уравнениям определяет­ся как учётом нелинейностей реальных характеристик элементов си­стемы, так и дополнительным введением в систему элементов с сущест­венно нелинейными характеристиками.

Обычно в первом случае нелинейности учитывают для рассмотре­ния изменения качества процесса управления за счёт влияния нелиней­ностей, присущих реальной системе, и исправления нежелательного эффекта, возникающего под влиянием этих нелинейностей.

Во втором случае речь идет о повышении качества процессов или о получении принципиально новых алгоритмов в управлении за счёт введения дополнительных нелинейных элементов. При этом удаётся повысить быстродействие и точность системы, уменьшить перерегули­рование или компенсировать нежелательное действие имеющихся нелинейностей.

Если в линейных системах работоспособными оказываются только устойчивые системы и появление нарастающих колебаний рассматривают как недопустимое явление, то в нелинейных системах вопрос об устойчивости ставят иначе.

Существует большое число нелинейных автоколебательных систем уп­равления, в которых колебания являются свойством нормального режима работы системы. В этом случае под устойчивой работой систе­мы понимают устойчивость автоколебаний в неустойчивой, с точки зрения линейной теории, системе. Само по себе определение устойчи­вости в этом случае изменяется. В линейных системах признаком устой­чивости является возврат системы в исходное состояние при сниже­нии внешнего воздействия до нуля.

Такую устойчивость называют асимптотической, или устойчи­востью в точке. Этим понятием можно пользоваться и для характе­ристики нелинейных систем.

Однако в нелинейных системах большее значение имеет устойчи­вость в некоторой области, характеризующаяся возвратом системы в заданную область при уменьшении внешнего воздействия до нуля. При оценке устойчивости обоих видов применяют понятия устойчиво­сти в малом, в большом и в целом, введенные в связи с рассмотрением процессов в нелинейных системах.

При изучении нелинейных систем неприменим принцип наложе­ния: при сложных воздействиях процесс в системе не может быть пред­ставлен как сумма процессов, получающихся от каждой из составля­ющих воздействия в отдельности. Это обстоятельство чрезвычайно ос­ложняет количественный анализ нелинейных систем автоматического управления.

Рассмотрим примеры систем автоматического управления, в которых надо учитывать нелинейность характеристик.

Система стабилизации курса. Для стабилизации курса корабля, торпеды или летательного аппарата применяются системы автомати­ческого управления рулями, обеспечивающие поддержание неизмен­ным заданного курса. Простейшая система стабилизации курса по­казана на рисунке 3.1.1, а.

Объект схематически изображен в виде корабля 1, ось которого со­ставляет угол с заданным курсом , фиксируемым гироскопическим компасом 2. Отклонение от курса воздействует при помощи усилителя гироскопического компаса на рулевую машинку 3, через соответствующую передачу, поворачивающую руль 4 кораб­ля на угол .

На рисунке 3.1.1, б схематически показан привод пневматической руле­вой машинки. Заслонка, управляющая подачей воздуха в рабочий цилиндр двигателя, поворачивается на угол , создавая этим перепад давления воздуха в рабочем цилиндре и перемещение y поршня. Пе­ремещение рабочего поршня ограничено упорами и может происхо­дить при .

Рисунок 3.1.1 – Управление курсом корабля

Зависимость между скоростью движения поршня и по­ложением управляющей заслонки выражается графиком (рисунок 3.1.1, в). При любом значении y, лежащем в пределах от до . эта зависимость сохраняется и имеет вид симметричной кривой с областями нечувствительности и насыщения. Однако как только рабочий поршень достигает упора, он останавливается; если дальнейшее изменение соответствует прижатию поршня к упору, то скорость поршня остает­ся равной нулю при любом значении .

Таким образом, скорость движения поршня является функцией двух переменных и выражается следующими уравнениями:

(3.1.1)

Переход с кривой на прямую происходит скачком при (штриховая линия на рисунке 3.1.1, в).

В системе передачи от рулевой машинки к перу руля могут быть за­зоры, создающие неоднозначную зависимость.

Таким образом, даже при упрощенном рассмотрении система ста­билизации курса содержит две нелинейности, обусловленные упорами и зазорами системы передачи.

Структурная схема рассматриваемой системы показана на рисунке 3.1.1, г. Здесь принято, что объект описывается инерционно-интегрирующим звеном 1, а усилитель гироскопа и корректирующая обратная связь по положению руля — пропорциональными звеньями 2, 5 с коэффициен­тами передачи и . Систему управления рулем описывают нелиней­ные звенья 3 и 4.

Случайные возмущающие воздействия, приведенные к углу пово­рота руля, обозначены составляющей f.

При изучении линейных систем рассматривались методы повыше­ния качества переходных процессов за счёт введения линейных коррек­тирующих устройств. Применение нелинейных элементов в схемах уп­равления значительно расширяет возможности повышения качества пе­реходных процессов в системе.

Нелинейная коррекция непрерывных систем. Рассмотрим отработку скачка простейшей следящей системой при двух различных значениях коэффи­циента усиления (рисунок 3.1.2, а).

При большом коэффициенте усиления (кривая ) процесс носит резко колебательный характер, величина перерегулирования велика и время , в течение которого наступает момент равенства и мало. При малом коэффициенте усиления (кривая ) процесс протекает апериодически, перерегулирование отсутствует, и время компенсации рассогласования велико. Естественно, возникает стремление создать такую систему, которая, имея высокий коэффициент усиления при больших рассогласованиях , уменьшала бы его по мере умень­шения рассогласования. В этом случае переходный процесс должен иметь вид кривой . Уменьшение коэффициента усиления по мере уменьшения рассогласования достигается включением нелинейного усилителя с характеристикой, представленной на рисунке 3.1.2, б.

Рисунок 3.1.2 – Нелинейная коррекция непрерывных систем

В системах автоматического управления встречаются нелинейности самого различ­ного вида. Будем характеризовать каждую нелинейность соответству­ющей функцией . При этом будем считать, что имеет место одно­мерная нелинейность, т.е. переменная z представляет собой функцию только одной переменной x. Возможны случаи и многомерных нелинейностей, когда переменная z — функция нескольких переменных.

Нелинейные звенья можно классифицировать по различным пока­зате­лям: симметрии, гладкости, однозначности характеристик. Рас­смотрим каждый из этих показателей.

Симметрия. Для нелинейных характеристик можно указать два типа симметрии:

1) если функция удовлетворяет условию

(3.1.2)

то такую характеристику называют симметричной относительно оси ординат, или чётно-симметричной.

2) если функция удовлетворяет условию

(3.1.3)

то характеристику назы­вают симметричной отно­сительно начала коорди­нат, или нечётно-симметричной.

Характеристики, не удовлетворяющие ни одному из приведенных усло­вий, называют несимметричными.

В ряде случаев путём перемещения координат несимметричные характеристики могут быть приведены к симметричным. Перемещение начала координат соответствует введению дополнительных слагаемых на входе и выходе звена. Например, для несимметричной характери­стики (рисунок 3.1.3, а, б) можно ввести подстановку так, чтобы полученная характеристика оказалась симметрич­ной относительно оси ординат. Такое преобразование координат соот­ветствует введению сигнала на входе звена и переходу от несиммет­ричной характеристики к чётно-симметричной (рисунок 3.1.3, в, г).

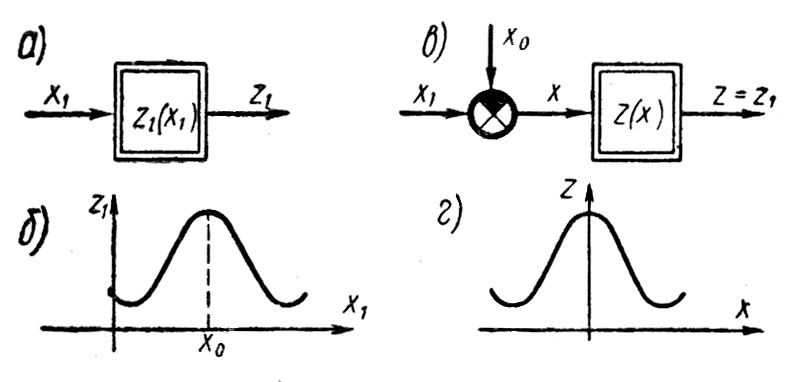
Рисунок 3.1.3 – Преобразование несимметричной статической характеристики в чётно-симметричную

Аналогично для характеристики (рисунок 3.1.4, а, б) можно путём подстановки и получить нечётно-симметричную характеристику . Структурная схема и характеристика , соответствующая данному преобразованию координат, показаны на рисунке 3.1.4, б и г.

Рисунок 3.1.4 – Преобразование несимметричной статической характеристики в нечётно-симметричную

Гладкость. Если в любой точке характеристики существует производная , то характеристика относится к гладким. Если на характеристике имеются изломы, в которых производная имеет разрыв, то характеристика относится к ломаным. Большую группу ломаных характеристик представляют кусочно-линейные характеристи­ки, состоящие из отрезков прямых.

В ряде случаев с целью облегчения расчёта гладкие характеристики бывает удобно приближенно заменять кусочно-линейными ломаными.

Однозначность. Если каждому значению x соответствует одно оп­реде­лён­ное значение z, то характеристику называют однозначной. Если каждому значению x соответствует несколько значений z в за­висимости от режима, предшествовавшего рассматриваемому моменту, то характеристику называют многозначной. При этом число возмож­ных значений z может лежать в пределах от 2 до .