Решение

При продаже всего выпуска по единой цене максимальную прибыль монополии представляет площадь прямоугольника FABE (см. рисунок), равная [21(63 - 21)] = 882.

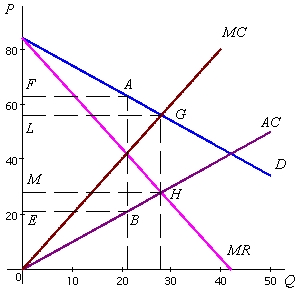
В случае осуществления дискриминации первой степени прибыль монополии соответствует площади фигуры KHGM, равной [28(56 - 28) + 0,5·28(84 - 56)] = 1176.

90. Монополия может продавать продукцию на двух сегментах рынка с различной эластичностью спроса: Q₁^D = 160 - P₁; Q₂^D = 160 - 2P₂. Ее функция общих затрат имеет вид TC = 5 + 5Q + 0,25Q².

1. При каких ценах на каждом из сегментов монополия получит максимум прибыли?  2. Сколько ед. продукции будет продаваться на каждом сегменте рынка при запрете ценовой дискриминации?

Решение

1. Условие максимизации прибыли при осуществлении ценовой дискриминации третьей степени следующее:

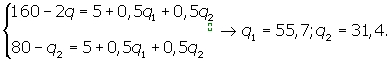
Оптимальные цены на сегментах рынка P₁ = 160 - 55,7 = 104,3; P₂ = 80 - 0,5·31,4 = 64,3. Прибыль монополии в этом случае будет π = 104,3·55,7 + 64,3·31,4 - 5 - 5·87,1 - 0,25·87,1² = 5491.

2. Для определения условий достижения максимума прибыли при запрете ценовой дискриминации выведем функцию суммарного спроса

Соответственно

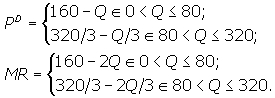
В этом случае линия MC = 5 + 0,5Q ломаную MR пересекает 2 раза

160 - 2Q = 5 + 0,5Q → Q* = 62; P* = 98; π = 98·62 - 5 - 5·62 - 0,25·62² = 4800;

320/3 - 2Q/3 = 5 + 0,5Q → Q* = 87,1; P* = 77,7; π = 77,7·87,1 - 5 - 5·87,1 - 0,25·87,1² = 4430,6.

Следовательно, в случае запрещения ценовой дискриминации на втором сегменте рынка продукция продаваться не будет.

96. Какую цену выгодно установить монополисту, если постоянные издержки составляют 250 тысяч рублей в год, переменные затраты на единицу товара - 5 рублей, а величина спроса при цене, равной 6 рублей достигает 300 тысяч штук в год и падает на 10 тысяч штук при увеличении цены на каждые 50 копеек? Учтите, что по данным исследования рынка, кривая спроса представляет собой отрезок прямой.

Решение:

Совокупные издержки монополиста состоят из постоянных и переменных издержек:

ТС = TFC + TVC

ТС = 250 000 + 5*Q

MC = dTC / dQ = 5

Составим уравнение прямой описывающей спрос:

P = a-bQ

Для этого составим систему уравнений:

6 = а - b * 300 000

21 = а - b * 0

а= 21

b= 0.00005

P = 21 - 0.00005*Q

TR = Р × Q = aQ - bQ²

тогда предельная выручка

MR =21 – 2*0,00005*Q

MR = 21- 0.0001Q

Условие максимизации прибыли для монополиста:

MC = MR

5 = 21 – 0.0001Q

Q = 160 000 шт.

Таким образом монополист установит объем выпуска Q= 160 000 шт. что соответствует цене P=13 рублей за ед.

116. В отрасли работают 10 фирм с одинаковыми функциями затрат TC_i = 4 + 2q_i + 0,5q²_i. Отраслевой спрос задан функцией: Q^D = 52 - 2P. Собственник одной из фирм предложил своим конкурентам передать ему свои предприятия, обещая за это выплачивать им регулярный доход, в 2 раза превышающий получаемую ими прибыль.

1. Насколько возрастет прибыль инициатора монополизации отрасли, если его предложение будет принято?

2. Насколько сократятся излишки потребителей?

Решение

1. Определим функцию предложения отдельной фирмы

Совместное предложение 10 фирм будет

В отрасли установится равновесие при

- 20 + Р = 52 - 2Р → P = 6; Q = 40; q_i = 4;

π = 6·4 - 4 - 2·4 - 0,5·16 = 4.

Когда все фирмы будут принадлежать одному продавцу, цена определиться из равенства MR = MC:

26 - Q = 2 + 0,1Q → Q = 21,82.

Тогда цена поднимется до (26 - 0,5·21,82) = 15,1. Прибыль монополиста составит

π = 15,1·21,82 - 40 - 2·21,82 - 0,05·21,822 = 222.

После выплат каждому из бывших конкурентов по 8 ден. ед. у монополиста останется (222 - 72) = 150, т.е. его прибыль возрастет в 150/4 = 37,5 раза.

2. Излишки потребителей в результате монополизации отрасли сократились с 400 до 119 ден. ед., т.е. на 281 ден. ед.

122. При линейной функции спроса монополия получает максимум прибыли, реализуя 10 ед. продукции по цене 24 ден. ед. Функция общих затрат монополии TC = 100 + 4Q + 0,25Q².

Определите:

• Как изменится цена блага, если с каждой проданной его единицы будет взиматься налог в размере 7 ден. ед.?

• Как изменится прибыль монополии?

• Какова сумма получаемого налога?

• Как изменятся излишки потребителей?