Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный областной университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

[ЭМЛ] Лекция 16.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

2.8 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

3. Приведение к конъюнктивной нормальной форме кнф

Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.

Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций.

Пример КНФ:

Пусть ДНФ F имеет вид ,

где - элементарные конъюнкции.

Процедура приведения ДНФ к КНФ:

1. Применить к F правило двойного отрицания

и привести

к ДНФ

где -элементарные конъюнкции. Тогда

2. С помощью правил де Моргана освободиться от второго отрицания и преобразовать отрицания элементарных конъюнкций в элементарные дизъюнкции D_1,D_2, ..., D_p.

Тогда

 …

Совершенной КНФ (СКНФ) называется КНФ, каждая элементарная дизъюнкция которой содержит все переменные.

4. Двойственность

Функция f *(х₁, ... , х_n) называется двойственной к функции f (х₁, ... , х_n), если

Отношение двойственности между функциями симметрично, т.е. если f * двойственна к f , то двойственна к f *:

Функция, двойственная к самой себе, называется самодвойственной.

Принцип двойственности:

если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула F* будет представлять функцию f *, двойственную f.

Принцип двойственности в булевой алгебре:

если в формуле F, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу F*, представляющую функцию f *, двойственную f.

Справедливо утверждение: если функции равны,

т.е. f₁ = f ₂, то и двойственные им функции равны,

т.е. f₁ * = f₂*.

Пример 1.

Доказать справедливость обобщенного склеивания (4.26) методом эквивалентных преобразований (используя основные эквивалентные соотношения (4.14) - (4.23)).

Решение Пример 1.

Выполним эквивалентные преобразования, указывая под знаком равенства номер используемого соотношения:

(4.20 a) (4.23) (4.16) (4.24 а)

Подтвердим справедливость использованного выше соотношения (4.24,а):

(4 20, а) (4 16) (4 20, в) (4 20, а)

Пример 2.

Получить СДНФ функции, используя эквивалентные соотношения:

F (x, y, z, u) = x y  x z  z u Решение Пример 2.

Для получения СДНФ воспользуемся расщеплением (склеиванием в обратную сторону) (4.23),

имея в виду также, что х = х 1 (4.20, а)

и (4.23).

Далее раскроем скобки, используя (4.16), и освободимся от одинаковых членов дизъюнкции на основании х  х = х (4.18, б):

F (x, y, z, u) = x y  x z  z u =

(4 25)

(4 26)



(4.18 б)

Пример 3.

Упростить булевы формулы:

а)

Решение Пример 3 а .

(4.24)

(4.27) (4.16)

(4. 23) (4. 20, а)

Пример 3 б

б)

Решение Пример 3 б

(4. 16)

(4. 22)

(4. 20, б.г)

(4. 18, a) (4. 24)

Пример 4.

Представить булеву формулу

в базисе {&, } и {, }. Сделать выводы.

Решение Пример 4.

Представим формулу базиса { &, , } в базисах

{ &, } и {, }, последовательно используя правила де Моргана (2.21,б) и (2.21, а) соответственно, а также правило двойного отрицания (2.19):

а)

б)

Булев базис { &, ,  } в некотором смысле “избыточен” - при удалении из него операции & или  функциональная полнота полученных систем {&,} и {v,} сохраняется. Однако в представлении { &, , } логические функции выражаются более простыми формулами, как это видно из примера.

За неизбыточность базисов операций приходится платить избыточностью формул: каждая замена одной операции на другую вносит в формулу лишние отрицания.

Пример 5.

Пусть логическая функция f (x, y, z) представлена формулой .

Требуется:

1) упростить формулу;

2) получить СДНФ, используя:

а) табличное представление функции f (x, y ,z),

б) расщепление (обратное склеивание).

Решение Пример 5.

1) Упростим формулу:

(4.27) (4.16) (4.23) (4.20)

Таким образом, f (x, y, z) = x  z.

Получим СДНФ функции:

а) расщеплением (обратным склеиванием):

б) табличным представлением функции

f (x, y, z) = x  z (табл. 4.12);

x, y, z	x  z
0 0 0	0
0 0 1	1
0 1 0	1
0 1 1	1
1 0 0	1
1 0 1	1
1 1 0	1
1 1 1	1

f = 1 на наборах {(0 0 1), (0 1 1), (1 0 0), (1 0 1), (1 1 0), (1 1 1)}, поэтому СДНФ функции f

Сравнивая результаты а) и б), убеждаемся в их идентичности. Таким образом, СДНФ функции

Пример 6.

Упростить СДНФ функции

Решение Пример 6.

Для эффективного упрощения СДНФ используем метод Блейка-Порецкого.

Метод заключается в попарном склеивании всех элементарных конъюнкций СДНФ между собой;

в получении элементарных конъюнкциях с меньшим числом переменных,

применение - поглощения конъюнкциями меньшего числа переменных конъюнкций большего числа переменных.

Рассмотрим метод Блейка-Порецкого “в действии”, для чего пронумеруем элементарные конъюнкции СДНФ:

1 2 3 4 5 6 7

Выполним все возможные попарные склеивания (4.25) элементарных конъюнкций в СДНФ (под результатом склеивания проставим номера склеиваемых конъюнкций):

1,6 1,7 2,3 2,4 2,5 3,7 4,6 4,7 5,6

Выполним все возможные попарные склеивания полученных элементарных конъюнкций трех переменных:

1,6 1,7 2,3 2,4 2,4 2,5

4,7 4,6 4,7 3,7 5,6 4,6

Очевидно, что дальнейшее склеивание в данном примере невозможно. Объединим символом  все полученные дизъюнкции элементарных конъюнкций.

Таким образом, в результате попарного склеивания получили:

Выполним теперь в этом выражении поглощение (4.24), в результате чего получим:

Пример 7.

Привести к ДНФ формулу:

Решение Пример 7.

Пример 8.

Привести формулу к КНФ:

Решение Пример 8.

Пример 9.

Рассуждение логически правильно, если формула, его представляющая, тождественно истинна, т.е. при любых значениях истинности своих простых высказываний принимает значение “истина”.

Подтвердить справедливость умозаключения из примера 2, § 4.2, используя метод эквивалентных преобразований:

((А  (В & (С  D))) &A) (CD).

Решение Пример 9.

Приведем логическую формулу к булевой форме с

помощью эквивалентного соотношения (4.6), получим ДНФ и упростим формулу, используя основные эквивалентные соотношения (4.14) - (4.23):

Таким образом, данное рассуждение логически правильно.

Пример 10.

Проверить правильность рассуждений, приведенных в примере 3 § 4.2:

((A (СВ))&(В(A&D))&(D(BC))&(AC))A.

Решение Пример 10.

Приведем посылку внешней импликации к булевой форме, используя соотношения (4.6) и (4.8),и упростим, используя основные эквивалентные соотношения:

Таким образом, после упрощения посылки формула рассуждения имеет вид:

что подтверждает правильность приведенного в примере 3 § 4.2 умозаключения относительно телевизионного сериала.

Пример 11.

Пусть.

Требуется:

а) получить СКНФ функции f;

б) построить таблицу истинности f;

в) сформулировать правило получения СКНФ функции, исходя из ее табличного представления.

Решение Пример 11

а)

б) Таблица истинности функции f (x, y, z) была получена в примере 5 (см. табл. 4.12).

в) Сравнивая СКНФ функции

f(x ,y ,z) = (х  у Ú z)(х Ú y Ú z)

и ее табличное представление, можно сделать вывод о том, что между нулевым множеством функции, определяемым ее таблицей, и СКНФ функции имеет место взаимно однозначное соответствие, очевидным образом определяющее требуемое правило получения СКНФ функции по ее таблице истинности:

СКНФ строится из элементарных дизъюнкций, соответствующих обратным наборам, на которых функция равна нулю.

Пример 12.

Для функции f(х) из упражнения 3 § 4.4,

Упражнение 3.

Найти СДНФ логических функций трех переменных

f₁– f₄, заданных в табл. 4.11.

x у z	f₁	f₂	f₃	f₄
0 0 0	0	0	1	0
0 0 1	0	0	0	1
0 1 0	0	1	0	0
0 1 1	1	1	1	1
1 0 0	1	0	1	1
1 0 1	0	1	0	0
1 1 0	1	1	1	1
1 1 1	1	1	0	0

заданной таблично (табл. 4.11), получить СКНФ.

Решение Пример 12.

Воспользуемся правилом, сформулированным в предыдущем примере. Нулевое множество функции f (x, y, z) в соответствии с табл. 4.11

включает наборы {(0 0 0), (0 0 1), (0 1 0), (11)}.

В таком случае в соответствии с правилом построения СКНФ, сформулированным в примере 11, получаем:

Пример 13. Получить СКНФ функции f (x, y, z, u) из примера 2.

Пример 2.

Получить СДНФ функции, используя эквивалентные соотношения:

F (x, y, z, u) = x y Ú x z Ú z u

В примере 2 для заданной функции

была получена СДНФ:

f (x, y, z) = =

Решение Пример 13.

Воспользуемся этими данными для получения СКНФ, для чего определим единичное множество функции

f (x, y, z, u) т.е. множество наборов,

на которых f = 1: {(1111), (110 1), (1 1 1 0), (1 1 0 0), (1 0 1 1), (1 0 1 0), (0 1 1 1), (0 0 1 1)}.

Всего наборов функции четырех переменных 2⁴ = 16. Определим теперь нулевое множество

для f (x, y, z, u) т.е. множество наборов,

на которых

f = 0: {(0 0 0 0), (0 0 0 1), (0 0 1 0), (0 1 0 0), (0 1 0 1), (0 1 1 0), (1 0 0 0), (1 0 0 1)}.

Отсюда по правилу построения СКНФ из нулевого множества функции:

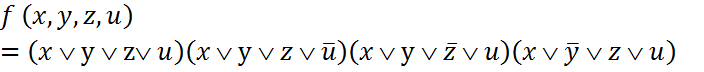
Пример 14.

Доказать справедливость принципа двойственности в булевой алгебре, исходя из общего принципа двойственности.

Решение Пример 14.

Булева алгебра (Р₂ ; &, , )

содержит три операции:  = { &, , ] }.

Для каждой операции булевой алгебры найдем двойственные им операции.

а) Пусть

б) Пусть

Тогда

в) Пусть

Тогда

Таким образом,

конъюнкция двойственна дизъюнкции,
дизъюнкция - конъюнкции,
отрицание самодвойственно.

Наконец, константы 0 и 1 принадлежат множеству логических функций Р₂ , поэтому 0 и 1 могут содержаться в булевой формуле и являются двойственными друг к другу: если ,