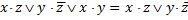16 Лекция
§ 4.5. Эквивалентные преобразования
Исследование логических формул и получение новых формул, эквивалентных данным необходимо при помощи корректных преобразований по двум правилам:
Правило №1 Правило подстановки формулы F вместо переменной х. |
Правило №2 Правило замены подформул.
|
При подстановке формулы F вместо переменной х все вхождения переменной х в исходное соотношение должны быть одновременно заменены формулой F. Правило применяется к эквивалентным соотношениям для получения новых эквивалентных соотношений. Например, стандартным методом была доказана эквивалентность соотношений:
Если вместо всех вхождений переменной х1 в данное соотношение подставить формулу
получим новое соотношение
также эквивалентное. |
Если какая-либо формула F, описывающая функцию f, содержит F1 в качестве подформулы, то замена F1 на эквивалентную F2 (F1 = F2 ) не изменит функции f; полученная при такой замене новая формула F эквивалентна исходной F. Правило замены подформул позволяет, используя известные эквивалентные соотношения, получать формулы, эквивалентные данной, в частности упрощать формулы, облегчая последующий анализ логической функции, и др. Эквивалентные преобразования - преобразования, использующие эквивалентные соотношения и правило замены. |
Эквивалентные преобразования (наряду со стандартным методом) - мощное средство доказательства эквивалентности формул.
Основные эквивалентные соотношения (законы) в булевой алгебре.
Ассоциативность конъюнкции и дизъюнкции: |
||
а |
x1 (х2 х3) = (x1 х2) х3 = x1 х2 х3 |
(4.14) |
б |
x1 (х2 х3) = (x1 х2) х3 = x1 х2 х3 |
|
Коммутативность конъюнкции и дизъюнкции: |
||
а |
x1 х2 = х2 x1 |
(4.15) |
б |
x1 х2= х2 x1 |
|
Дистрибутивность конъюнкции относительно дизъюнкции: |
||
|
x1 (х2 х3) = x1 х2 x1 х3 |
(4.16) |
Дистрибутивность дизъюнкции относительно конъюнкции: |
||
|
x1(х2 х3) =(x1 х2) (x1 х3) |
(4.17) |
Идемпотентность: |
||
а |
x x = x |
(4.18) |
б |
x Ú x = x |
|
Закон двойного отрицания: |
||
|
|
(4.19) |
Свойства констант 0 и 1: |
||
а |
x × 1= x |
(4.20) |
б |
x × 0 = 0 |
|
в |
x 1 = 1 |
|
г |
x 0 = x |
|
д |
|
|
е |
|
|
Правила де Моргана: |
||
а |
|
(4.21) |
б |
|
|
Закон противоречия: |
||
|
|
(4.22) |
Закон исключенного третьего: |
||
|
|
(4.23) |
Основные эквивалентные соотношения (4.14) - (4.23) отличаются тем, что:
а) они не выводимы друг из друга;
убедиться в их справедливости можно,
используя стандартный метод доказательства эквивалентности формул;
б) этих соотношений достаточно для выполнения любых эквивалентных преобразований:
для любых эквивалентных формул F1 и F2 существует эквивалентное преобразование F1, в F2 с помощью соотношений (4.14) - (4.23).
Другие соотношения, часто применяемые в преобразованиях булевых формул, выводимы с помощью основных законов.
Примеры и способы решения задач эквивалентных преобразований в булевой алгебре
Эквивалентные преобразования |
|||
1. Упрощение формул для упрощения формул часто используются эквивалентные соотношения, выводимые из основных с помощью эквивалентных преобразований: |
|||
эквивалентное соотношение поглощение |
а |
x x y= x |
(4.24) |
б |
x (x y ) = x |
||
эквивалентное соотношение склеивание |
|
|
(4.25) |
эквивалентное соотношение обобщенное склеивание |
|
|
(4.26) |
|
|
(4.27) |
|
Эквивалентные преобразования |