Государственное бюджетное образовательное учреждение

среднего профессионального образования Московской области

«Ступинский авиационно-металлургический техникум им. А.Т.Туманова»

Методическое описание

к практическому занятию № 8

по дисциплине «Статистика»

тема: «Построение и определение уровней рядов динамики».

(6 часов)

Рассмотрено цикловой комиссией

«ОП и СД специальности 230103 и 230401»

Протокол заседания № от « » 2012 г.

Председатель цикловой комиссии Т.А.Еникеева

Преподаватель М.Г.Горюнова

2012

Практическое занятие № 8 Тема: «Построение и определение уровней рядов динамики».

1. Цель занятия: научиться определять виды рядов динамики и

рассчитывать показатели анализа рядов

динамики.

II. Постановка задачи.

1. Определить скорость и интенсивность развития рядов динамики.

2. Определить основную тенденцию ряда динамики,

связи между явлениями.

3. Провести анализ рядов динамики.

III. Содержание отчёта.

• конспект методических указаний.

• решение задач по определению показателей рядов динамики.

• анализ полученных данных.

IV. Порядок выполнения задания.

1. Прочитать и законспектировать методические указания.

2. Решение задач по определению показателей рядов динамики.

3. Формулировка выводов и анализ рядов динамики.

Методические рекомендации.

Различные явления, изучаемые статистикой, претерпевают непрерывные изменения во времени – изменяется их объем, состав, структура. Исходной базой для выявления и измерения этих процессов служат ряды динамики. Рядом динамики называется ряд изменяющихся во времени значений какого-либо показателя.

Составными элементами ряда динамики являются значения показателя, называемые уровнями ряда динамики, и показатели времени, к которым относятся уровни. Ряды динамики могут быть моментные и интервальные. В первом случае они характеризуют явление по состоянию на определенные моменты времени (например, данные о численности скота по состоянию на 1 января за ряд лет), а во втором – размеры явления за определенные интервалы времени (например, валовой сбор зерна за ряд лет). Уровни ряда динамики могут быть выражены в форме абсолютных, относительных или средних величин.

Построение и анализ рядов динамики производится для изучения изменений явлений во времени, выявления закономерностей и характерных особенностей их развития. Это достигается расчетом специфических показателей динамики и обработкой статистическими методами , позволяющими проявить закономерности изменения явления во времени. К таким показателям относятся абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста и средние показатели ряда динамики (средний уровень, средний абсолютный прирост, средний темп роста, средний темп прироста).

Абсолютный прирост – это разница между каждым последующим уровнем и уровнем, непосредственно предшествующим ему, или каждым данным уровнем и одним и тем же уровнем, принятым за базу сравнения. В первом случае абсолютные приросты называются цепными, во втором – базисными. Если абсолютный прирост обозначить А, уровень – у, тогда

цепные А₁=у₁-у₀; А₂=у₂-у₁; А₃=у₃-у₂ и т.д.;

базисные А₁=у₁-у₀; А₂=у₂-у₀; А₃=у₃-у₀.

Сумма цепных абсолютных приростов равна разности между конечными и начальными уровнями .

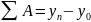Средний абсолютный прирост ряда динамики равен:

, или , где

n – число уровней.

Темп прироста (коэффициент или процент) – это отношение последующего уровня к предыдущему:

; ; … ; .

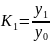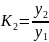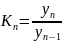Как и показатели абсолютного прироста, темпы роста могут быть цепными и базисными. Особенностью цепного ряда коэффициентов роста является то, что произведение его членов равно отношению крайних уровней:

.

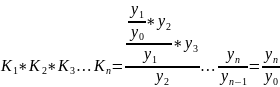Средний темп роста вычисляется по формуле средней геометрической:

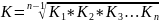, или ,

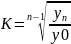где п — число уровней ряда динамики.

Темп прироста — отношение абсолютного прироста к предыду­щему уровню. Может быть выражен в виде коэффициентов или в процентах:

коэффициент прироста , или Т₁=К₁-1;

процент прироста 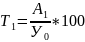, или Т₁=(К₁-1)*100

Абсолютное значение одного процента прироста есть частное от деления абсолютного прироста на темп прироста:

; ; …;

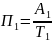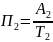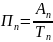
Этот показатель представляет собой сотую часть предыдущего уровня:

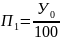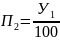; ; и т.д.

Средний уровень ряда динамики с равноотстоящими (по вре­мени) уровнями рассчитывается по формулам:

для интервального ряда динамики по средней арифметической простой

;

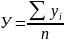
для моментного ряда динамики по средней хронологической

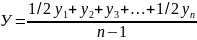
Для моментного ряда динамики с неравноотстоящими уровнями: (например, уровни даны на 1 января, на 1 апреля, на 1 июня) средний уровень ряда динамики рассчитывается по средней арифметической взвешенной:

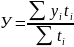где t_i — время, в течение кото­рого сохраняется без изменения каждый уровень ряда.

Являясь исходной базой для характеристики развития явлений во времени, ряды динамики используются для выявления основной тенденции развития, для измерения сезонных колебаний и харак­теристики некоторых других особенностей развития различных явле­ний (социально-экономических, технических, биологических и т. п.). Решение этих задач в ряде случаев требует применения специаль­ных приемов обработки и анализа рядов динамики.

В связи с тем, что основная тенденция развития некоторых явлений в силу каких-либо объективных причин (например, влияние метеоусловий на уровень урожайности) затушевывается, важное значение в анализе динамических рядов имеют статистические мето­ды проявления общей тенденции развития явлений, к которым от­носятся:

1. Укрупнение периодов. Суть этого метода заключается в том, что уровни исходного динамического ряда объединяются по более крупным периодам. Например, сравнивают уровни урожайности не за отдельные годы, а в среднем по пятилетиям. Особое внимание при этом следует обращать на обоснование периодов укрупнения. Например, поскольку плодоношение садов в ряде случаев подверже­но периодическим колебаниям, нельзя брать период с нечетным числом лет. При подобных циклических колебаниях в большинстве случаев интервал берут равным продолжительности цикла. В общем укрупненный интервал должен обеспечивать взаимное погашение случайных отклонений уровней.

2. Сглаживание ряда динамики методом скользящей средней. Суть метода заключается в том, что при расчете каждого последующего сглаженного уровня принятый для укрупнения период сдвигается на одну дату. Например, при сглаживании по трехлетиям

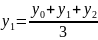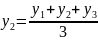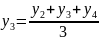, , и т.д.

3. Выравнивание по среднему абсолютному приросту динами­ческого ряда. Применяется в случае равномерного развития явле­ния, т. е. когда цепные абсолютные приросты динамического ряда близки по своим

значениям. Выравненные уровни (У_t) определяют­ся по формуле

где t — порядковый номер даты (t =1,2,..., n).

4. Выравнивание ряда динамики по среднему коэффициенту роста. Применяется в случае равноускоренного изменения ряда динамики, т. е. когда цепные темпы роста близки между собой.

Выравненные уровни определяются по формуле

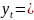
5. В ыравнивание ряда динамики способом наименьших квад­ратов. Сущность этого способа заключается в том, что подбирается уравнение, которое наиболее полно отражает характер изменения динамического ряда за изучаемый период. Таким уравнением, в частности, может быть уравнение прямой линии y_t=a+b*t, где

y _t — выравненное по уравнению значение динамического ряда; t— продолжительность времени; а и b — параметры уравнения, которые необходимо определить.

З атем выдвигается требование, чтобы сумма квадратов откло­нений выравненного по уравнению динамического ряда от факти­ческого имела минимальное значение: ∑(у-y_t)²=min.

Прием определения параметров уравнения, когда должно быть выполнено условие минимального расхождения между фактическими и расчетными параметрами, получил название способа наименьших квадратов. Требованию ∑(у-y_t)²=min удовлетворяет система нор­мальных уравнений:

∑y=na+b∑t;

∑yt=a∑t+b∑t².

Чтобы определить параметры уравнения а и b, надо решить данную систему нормальных уравнений.

Аналитическое выравнивание может быть проведено с исполь­зованием различных функций (линейной, показательной, логариф­мической, параболы и т. д.). Выбор функции определяется харак­тером изменения ряда динамики.

Для сравнительной характеристики развития явлений во вре­мени часто проводят сопоставления нескольких рядов динамики, причем предварительно приводят их к одному основанию, т. е. выражают уровни сравниваемых рядов в процентах или коэффи­циентах к одной и той же базе сравнения. При этом важное зна­чение имеет выбор базы сравнения, от которой во многом зависят численные значения темпов роста.

Смыкание рядов динамики применяется в случаях, когда дан­ные ряда динамики относятся к различному кругу объектов или рассчитаны по разной методике. Например, при изучении длительной динамики поголовья скота в колхозах нужно учесть, что происходи­ла реорганизация колхозов в совхозы; при изучении динамики ва­ловой продукции сельского хозяйства следует принять во внимание то, что периодически меняются сопоставимые цены на эту продук­цию. Суть метода состоит в том, что за один из периодов, в кото­ром изменился круг объектов или методика расчета показателей, определяют размер показателей как по кругу до изменения состава объектов, так и после, как по старой методике, так и по новой и затем, приняв полученные данные за базу сравнения, рассчитывают базисные темпы роста отдельно для каждого круга учитываемых объектов. В результате этого образуется непрерывный ряд отно­сительных величин, характеризующий изменение размера того или иного показателя за весь изучаемый период.

Важную роль в изучении рядов динамики играет сопоставление нескольких параллельных рядов. Например, уровня кормления коров и надоев молока, уровня внесения удобрений и урожайности, уровня интенсивности и экономической эффективности сельскохозяйственного производства и т. п.

В развитии многих явлений имеют место внутригодичные ­периодические колебания, получившие название сезонности. Например удои молока снижаются в зимний период и увеличиваются в летний, наоборот, затраты грубых кормов возрастают зимой и уменьшаются в летний период и т. п. Для измерения сезонных колебаний исполь­зуются обычно приемы сопоставления уровня каждого месяца со среднегодовым.

При построении и анализе рядов динамики необходимо обеспечить сопоставимость показателей по содержанию, единицам изме­рения, территории, кругу объектов, критическому моменту регист­рации, методике расчета, определению единиц совокупности и т.п.