Правило Лопиталя
Вычислить пределы с помощью правила Лопиталя:
281.
|
282.
|
283.
|
284.
|
285.
|
286.
|
287.
|
288.
|
289.
|
290.
|
291.
|
292.
|
293.
|
294.
|
295.
|
296.
|
297.
|
298.
|
299.
|
300.
|
301.
|
302.
|
303.
|
304.
|
305.
|
306.
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Ответы. 281.
.
282. 0. 283. 1. 284.
.
285.
.
286.
.
287.
.
288.
.
289.
.
290.
.
291.
.
292.
.
293.
.
294.
.
295.
.
296.
.
297.
.
298.
.
299.
.
300.
.
301.
.
302.
.
303.
.
304.
.
305.
.
306.
.
Исследование функций и построение их графиков
Найти интервалы возрастания и убывания функции:
307.
|
308.
|
309.
|
310.
|
.
.
.
.
Найти точки экстремума функции:
311.
.
312.
.
313.
.
314.
,
.
Найти интервалы выпуклости и вогнутости функции:
315.
.
316.
.
317.
.
318.
.
Найти точки перегиба функции:
319.
|
320.
|
321.
|
322.
|
.
.
.
.
Найти асимптоты линий:
323.
.
324.
.
325.
.
326.
.
Провести полное исследование функций и построить их графики:
327.
.
328.
.
329.
.
330.
.
331.
.
332.
.
333.
.
334.
.
335.
.
336.
.
Построить схематично
график непрерывной функции на интервале
,
если
337.
|
338.
,
|
339.
|
340. , , . |
,
,
.
,
.
,
,
.
341.-343.
Функция
непрерывна, дан график
.
Сколько точек экстремума у этой функции?
341.
|
342.
|
343.
|
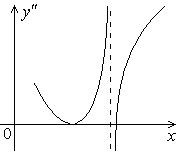
344.-346.
Функция
непрерывна, дан график
.
Сколько точек перегиба у этой функции?
344.
|
345.
|
346.
|
Ответы. 307. Функция убывает
при
.
308. Функция возрастает при
.
309. Функция возрастает при
,
функция убывает при
.
310. Функция возрастает при
,
функция убывает при
.
311.
,
.
312.
.
313.
.
314.
,
.
315. Функция вогнута при
,
функция выпукла при
.
316. Функция
выпукла при
.
317. Функция выпукла при
,
функция
вогнута при
.
318. Функция вогнута при
.
319.
.
320. Точек перегиба нет. 321.
Точек перегиба нет. 322.
,
.
323.
.
324. x=2,
y=3.
325.
,
.
326.
,
.
327. ОДЗ:
;
график симметричен относительно оси
;
;
вертикальные асимптоты
;
горизонтальная асимптота
.
328. График симметричен относительно
начала
координат;
,
;
точки перегиба
;
- горизонтальная
асимптота. 329. ОДЗ:
;
;
точка перегиба
;
- вертикальная
асимптота. 330. ОДЗ:
;
график симметричен относительно оси
;
;
точек перегиба нет; - вертикальная асимптота. 331. График симметричен относительно
оси
;
;
точки перегиба
;
асимптот нет. 332. ОДЗ:
;
экстремумов
нет; точек перегиба нет; вертикальная
асимптота
;
горизонтальные асимптоты
,
.
333. График симметричен относительно
начала координат;
;
;
точка перегиба
;
- наклонные асимптоты. 334.
,
;
- горизонтальная асимптота; точки
перегиба
.
335. ОДЗ:
;
;
точек перегиба нет; вертикальная
асимптота
,
горизонтальная асимптота
.
336.
,
;
точка перегиба
,
горизонтальная асимптота
.
341. 3. 342. 4. 343. 2. 344.
Нет. 345. 2. 346. 2.