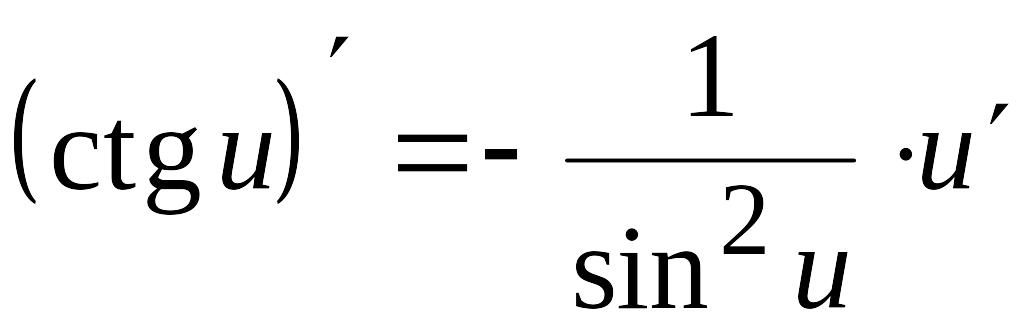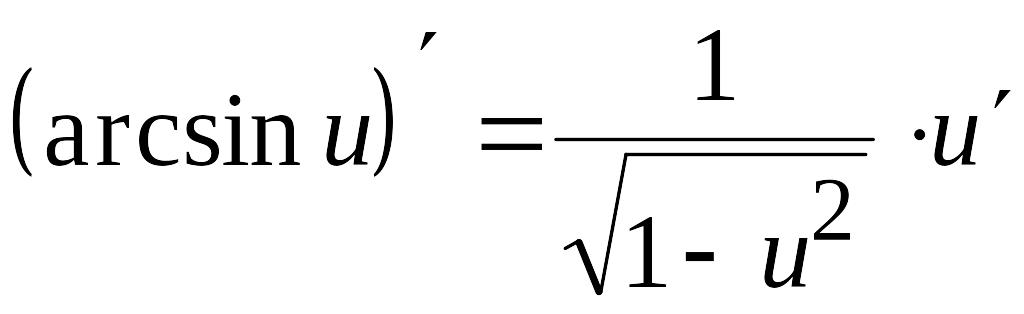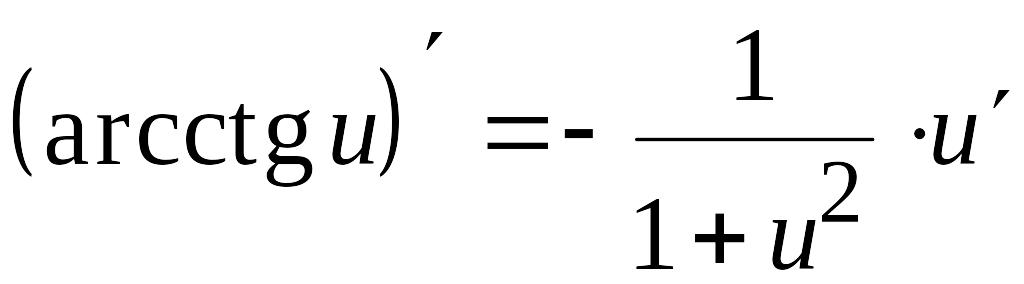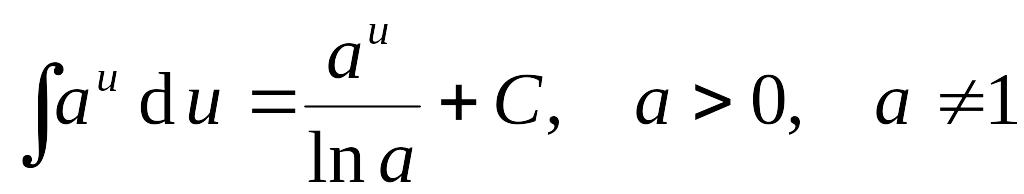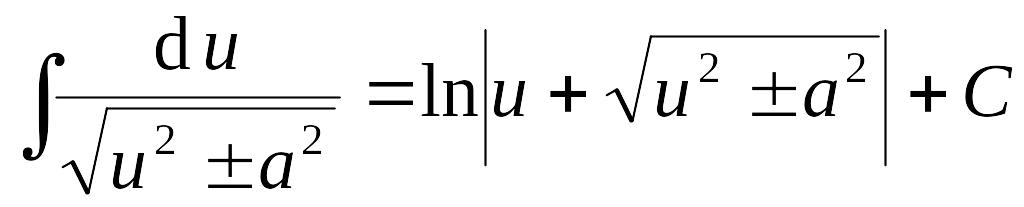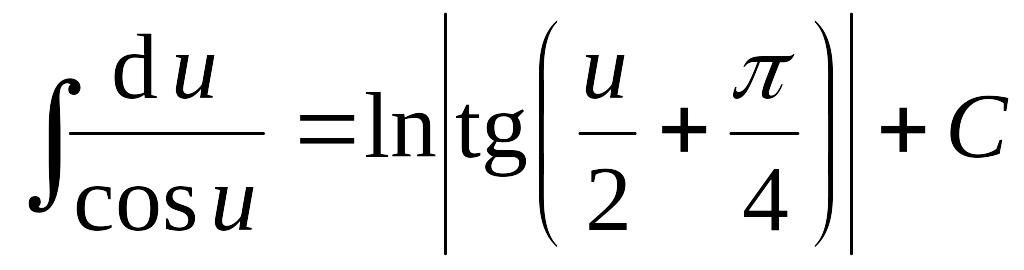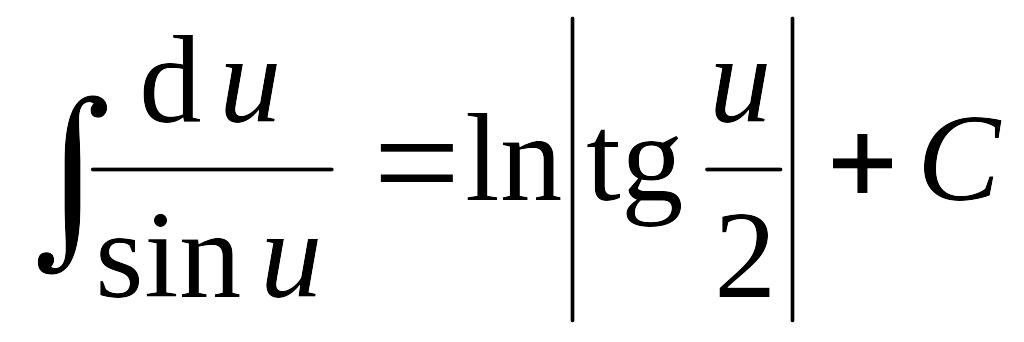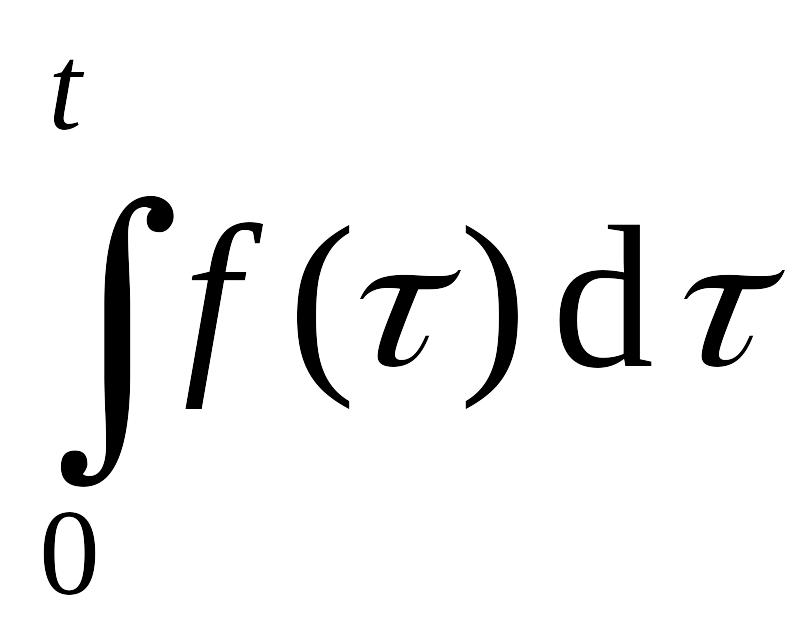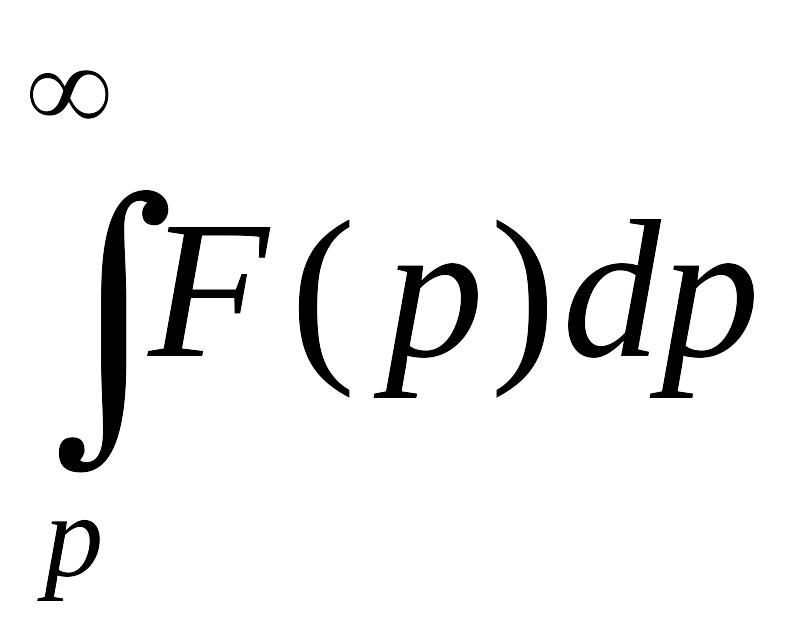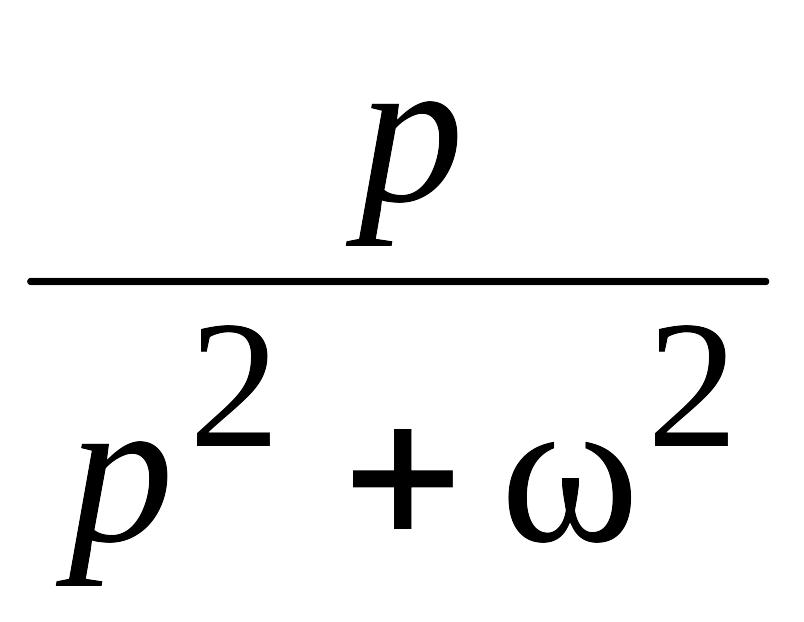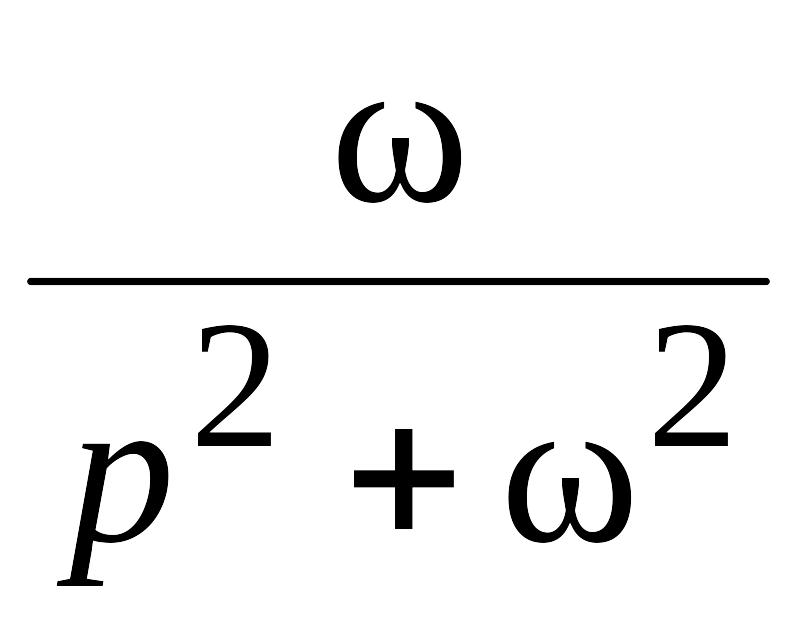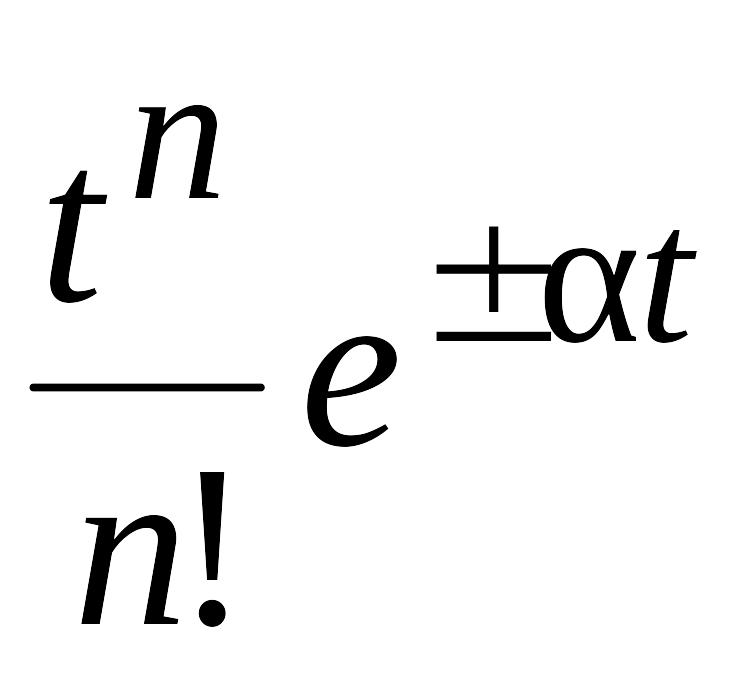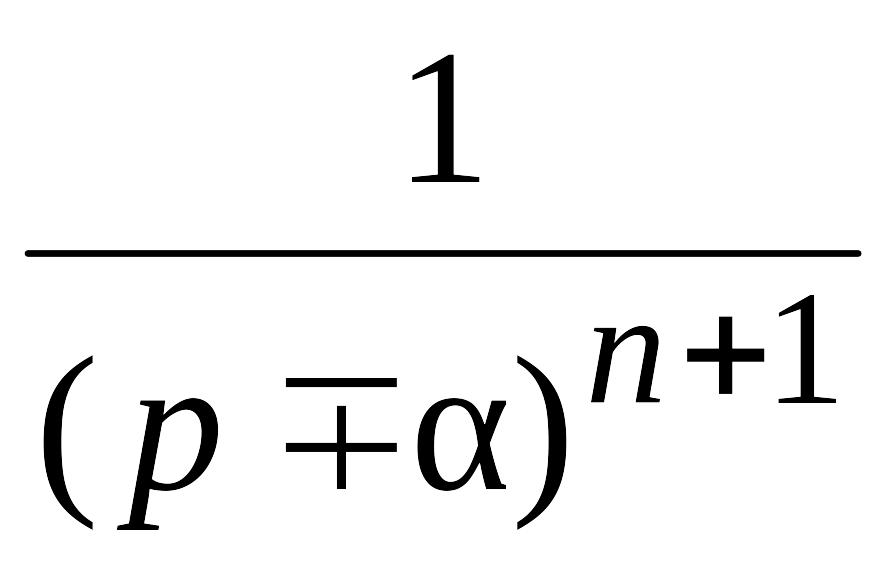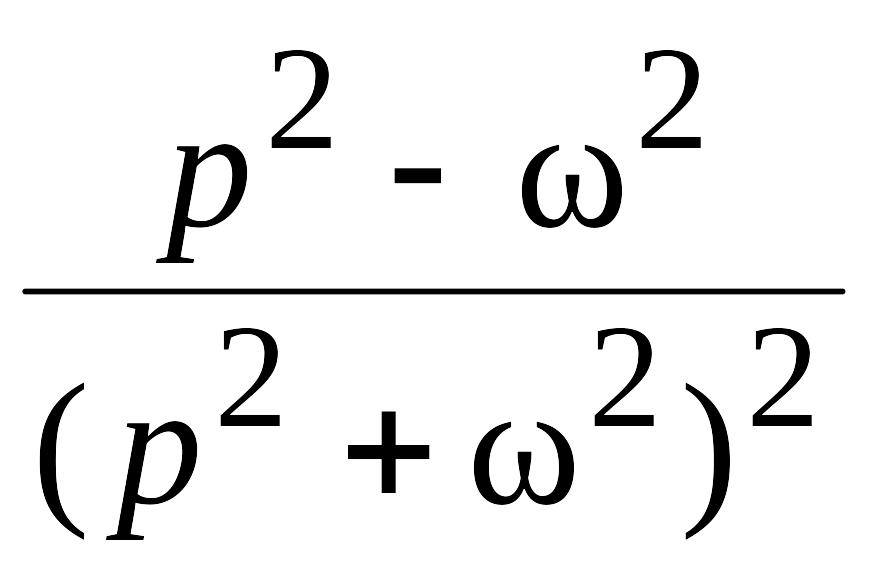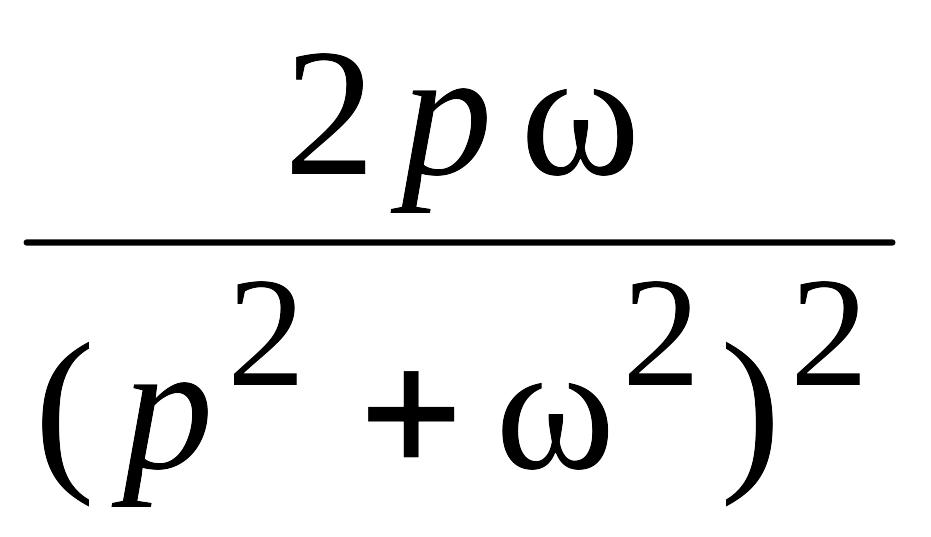Дифференцирование функций

Правила дифференцирования

1) вынесение постоянного множителя за знак производной:

2) производная суммы (разности) двух функций: u'v'

3) производная произведения двух функций: u'v+uv'

4) производная частного двух функций:

Таблица производных

1. C' = 0 2. (ua)' = aua1u', a 3. 4. 5. (au)' = au ln au', a > 0, a 1 6. 7. (loga u)' = a>0, a 1 8. (ln u)' =

9. 10. 11. 12. 13. 14. 15. 16.

Исследование функций и построение их графиков

Схема полного исследования функции:

1. Область определения.

2. Нули и интервалы знакопостоянства.

3. Точки разрыва и интервалы непрерывности.

4. Четность, нечетность.

5. Периодичность.

6. Исследование с помощью первой производной: интервалы монотонности, точки экстремума.

7. Исследование с помощью второй производной: интервалы выпуклости и вогнутости, точки перегиба.

8. Асимптоты.

9. Построение графика.

Неопределенный интеграл

Правила интегрирования

1) Интеграл суммы двух функций равен сумме интегралов от каждой функции:

2) Постоянный множитель можно выносить и вносить за знак неопределенного интеграла:

3) интегрирование по частям:

Таблица интегралов

1. 2. 3. 4. 5. 6. 7. 8. 9.

10. 11. 12. 13. 14. 15. 16. 17.

Операционное исчисление

Основные свойства преобразования Лапласа

, , ,

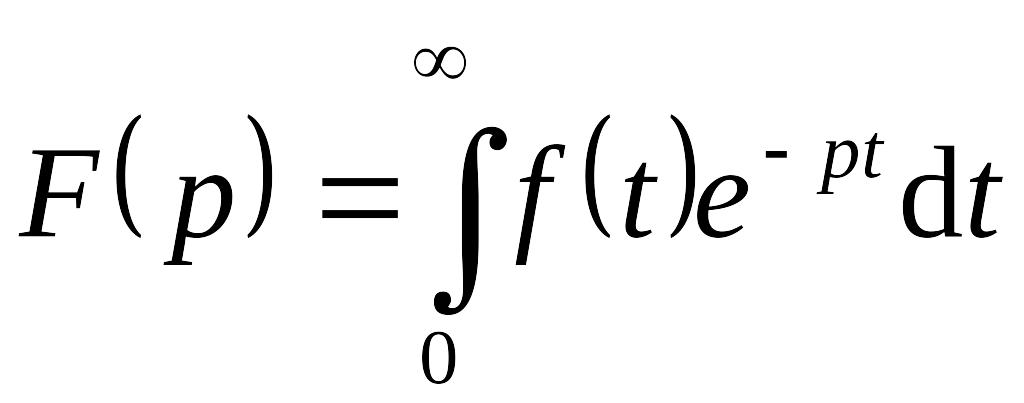Название свойства или теоремы	Оригинал f(t)	Изображение F(p)
1. Линейность
2. Теорема подобия
3. Теорема запаздывания (сдвига)
4. Теорема затухания (смещения)
5. Дифференцирование оригинала
6. Интегрирование оригинала
7. Дифференцирование изображения
8. Интегрирование изображения
9. Теорема свертывания

Изображения основных функций

№ п/п	Оригинал f(t)	Изображение F(p)		№ п/п	Оригинал f(t)	Изображение F(p)
1	1			7
2				8
3				9	t
4				10
5	t			11
6				12

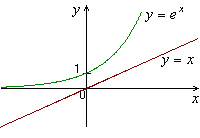
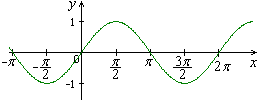
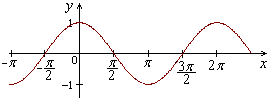
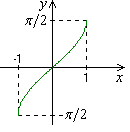
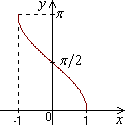
Приложение 1. Некоторые элементарные функции.

Частный случай:	Частный случай:

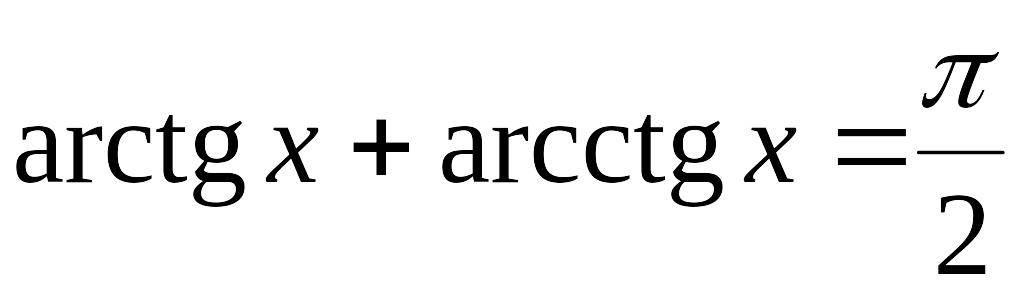
Приложение 2. Значения тригонометрических функций.

	0
	1				0				-1		0		1
	0				1				0		-1		0
	0		1		-		-1		0	1	-	-1	0
	-		1		0		-1		-	1	0	-1	-

Приложение 3. Некоторые тригонометрические формулы.

.

Приложение 4. Разложение на множители.

1) , где - корни квадратного уравнения

2)

3)

4) вынесение общего множителя

Приложение 5. Некоторые свойства логарифмов.

1) 2)

3) 4)

5)

Приложение 6. Действия со степенями.

1) 2)

3)

4) 5)

6) 7)