
- •Т.Э.Захарова математический анализ Учебное пособие
- •Комплексные числа
- •Функции одной переменной
- •Предел функции. Раскрытие неопределенностей. Замечательные пределы
- •Сравнение бесконечно малых и бесконечно больших величин
- •Непрерывные функции. Точки разрыва
- •Дифференцирование функций
- •Правило Лопиталя
- •Исследование функций и построение их графиков
- •Функции двух переменных
- •Неопределенный интеграл. Простейшие методы интегрирования
- •Неопределенный интеграл. Интегрирование по частям
- •Неопределенный интеграл. Интегрирование дробно-рациональных функций
- •Неопределенный интеграл. Интегрирование тригонометрических функций
- •Неопределенный интеграл. Интегрирование иррациональных функций
- •Определенный интеграл
- •Приложения определенного интеграла
- •Несобственные интегралы
- •Двойной интеграл
- •Тройной интеграл
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения второго порядка
- •Операционное исчисление
- •Комплексные числа.
- •Дифференцирование функций
- •Исследование функций и построение их графиков
- •Неопределенный интеграл
- •Операционное исчисление
- •Список литературы
- •Математический анализ Учебное пособие
- •630102, Новосибирск, ул.Кирова, 86
Операционное исчисление
766.-785. Найти изображения функции:
766.
|
767.
|
768.
|
769.
|
770.
|
771.
|
772.
|
773.
|
774.
|
775.
|
776.
|
777.
|
778.
|
779.
|
780.
|
781.
|
782.
|
783.
|
784.
|
785.
|
786.-797. Найти оригинал по изображению:
786.
|
787.
|
788.
|
789.
|
790.
|
791.
|
792.
|
793.
|
794.
|
795.
|
796.
|
797.
|
798.-803. Решить дифференциальные уравнения:
798.
|
799.
|
800.
|
801.
|
802.
|
|
803.
|
|
804.-807. Решить системы дифференциальных уравнений:
804.
![]() .
.
805.
![]() .
.
806.
![]() .
.
807.
![]() .
.
808.-810. Вычислить несобственный интеграл:
808.
![]() .
809.
.
809.
![]() .
810.
.
810.
![]() .
.
Ответы. 766.
![]() .
767.
.
767.
![]() .
768.
.
768.
![]() .
769.
.
769.
![]() .
770.
.
770.
![]() .
.
771.
![]() .
772.
.
772.
![]() .
773.
.
773.
![]() .
774.
.
774.
![]() .
775.
.
775.
![]() .
.
776.
![]() .
777.
.
777.
![]() .
778.
.
778.
![]() .
779.
.
779.
![]() .
780.
.
780.
![]() .
.
781.
![]() .
782.
.
782.
![]() .
783.
.
783.
![]() .
784.
.
784.
![]() .
785.
.
785.
![]() .
.
786.
![]() .
787.
.
787.
![]() .
788.
.
788.
![]() .
789.
.
789.
![]() .
.
790.
![]() .
791.
.
791.
![]() .
792.
.
792.
![]() .
793.
.
793.
![]() .
794.
.
794.
![]() .
.
795.
![]() .
796.
.
796.
![]() .
797.
.
797.
![]() .
.
798.
![]() .
799.
.
799.
![]() .
800.
.
800.
![]() .
801.
.
801.
![]()
![]() .
802.
.
802.
![]() .
803.
.
803.
![]() .
.
804.
![]() .
805.
.
805.
![]() .
806.
.
806.
![]()
![]()
![]() .
807.
.
807.
![]() .
808.
.
808.
![]() .
809.
.
809.
![]() .
810. 0.
.
810. 0.
СПРАВОЧНЫЙ МАТЕРИАЛ
Комплексные числа.
Комплексным
числом
![]() называется число вида
называется число вида
![]() ,
где
,
где
![]() и
и
![]() - действительные числа. Число
называется действительной
частью
комплексного числа
- действительные числа. Число
называется действительной
частью
комплексного числа
![]() (
(![]() ),
- мнимой
частью
комплексного числа
(
),
- мнимой
частью
комплексного числа
(![]() ),
),
![]() - мнимая
единица,
обладающая свойством
- мнимая
единица,
обладающая свойством
![]() .
.
Комплексные
числа
и
![]() являются взаимно сопряженными.
являются взаимно сопряженными.
Рис.1 |
Комплексное
число
Каждой точке
комплексной плоскости соответствует
радиус-вектор этой точки; его длина
называется модулем
комплексного
числа
,
обозначается
|
Угол между
радиус-вектором и положительным
направлением действительной оси
называется аргументом
комплексного
числа
и обозначается
![]() .
Главным
значением аргумента
является
значение
из интервала
.
Главным
значением аргумента
является
значение
из интервала
![]() ,
которое обозначается
,
которое обозначается
![]() (
(![]() ).
Таким образом,
).
Таким образом,
![]() ,
,
![]() .
.
Угол
|
|
Формы записи комплексных чисел:
1. ![]() - алгебраическая
форма;
- алгебраическая
форма;
2. ![]() - тригонометрическая
форма;
- тригонометрическая
форма;
3. ![]() - показательная
форма.
- показательная
форма.
Тригонометрическая
и показательная формы комплексного
числа связаны формулой
Эйлера:
![]() .
.
Действия над комплексными числами:
1. Числа заданы в
алгебраической форме (![]() и
и
![]() ):
):
Сумма
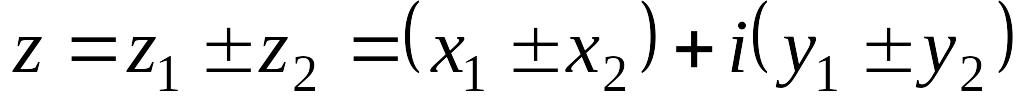 ;
;Произведение
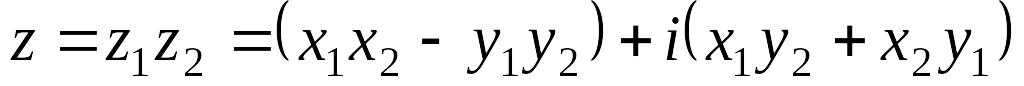 ;
;Частное
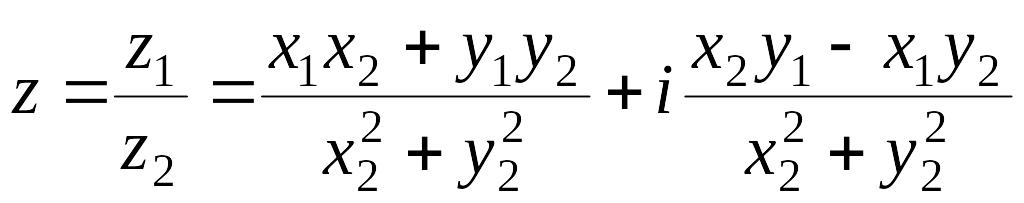 ,
где
,
где
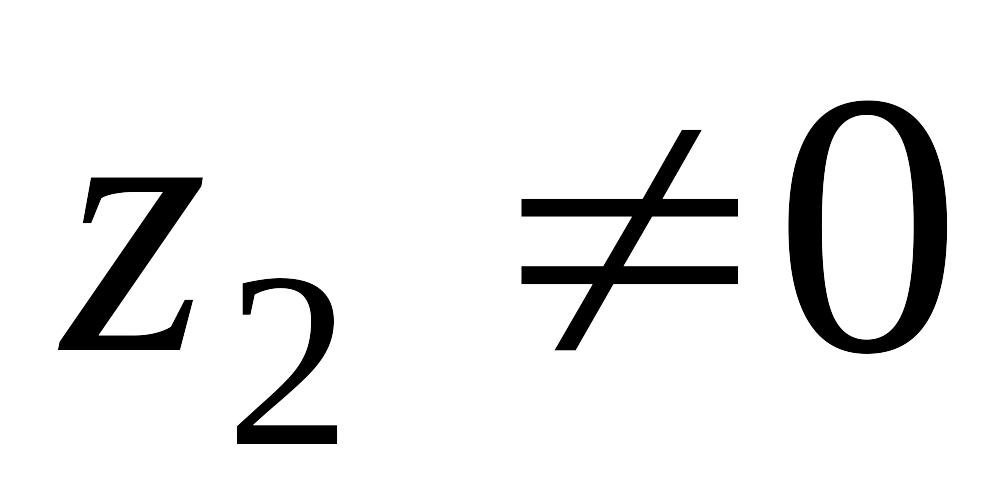 .
.
2. Числа
заданы в тригонометрической форме (![]() и
и
![]() ):
):
Сумма
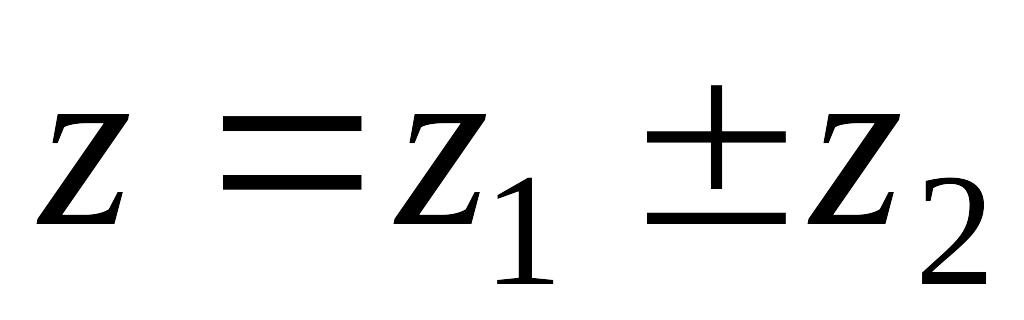 (как в алгебраической форме);
(как в алгебраической форме);Произведение
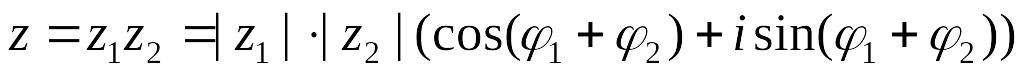 ;
;Частное
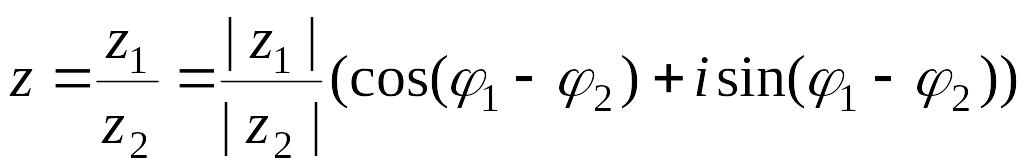 .
.
3. Числа
заданы в показательной форме (![]() ,
,
![]() ):
):
Сумма (как в алгебраической форме);
Произведение
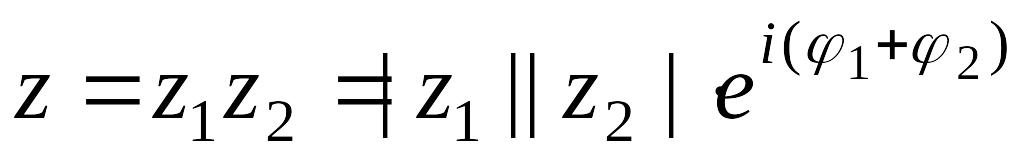 ;
;Частное
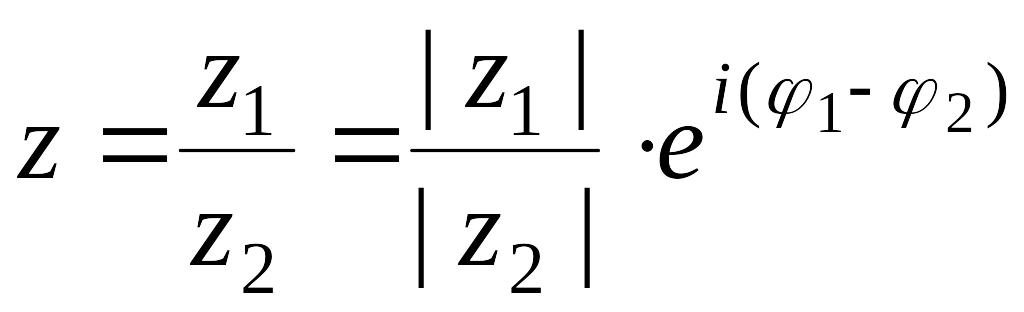 .
.
Возведение комплексных чисел в целую положительную степень определяется формулами:
если
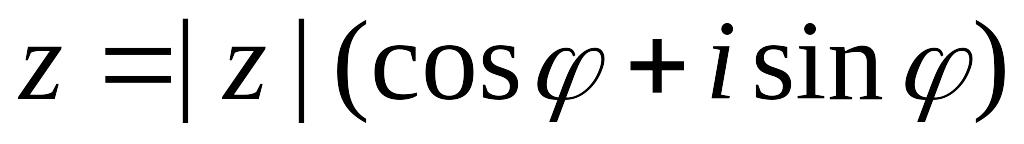 ,
то
,
то
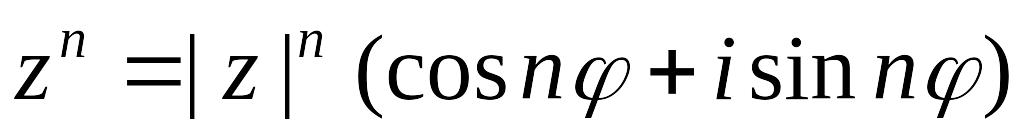 ;
;если , то
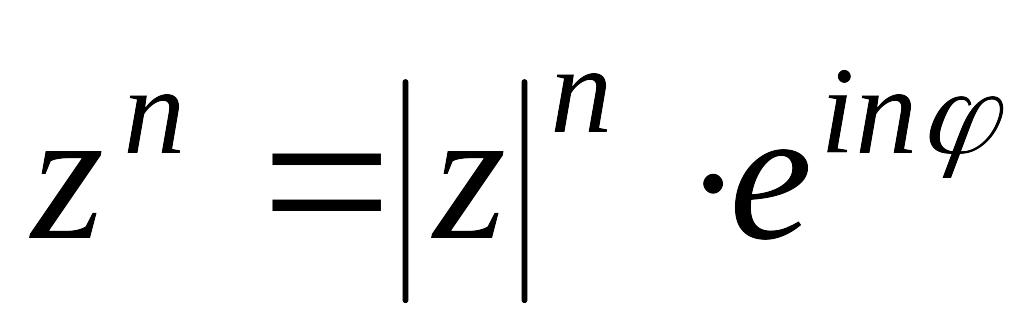 .
.
\Корень
![]() -ой
степени
из
имеет
различных значений, которые находятся
по формулам:
-ой
степени
из
имеет
различных значений, которые находятся
по формулам:
если
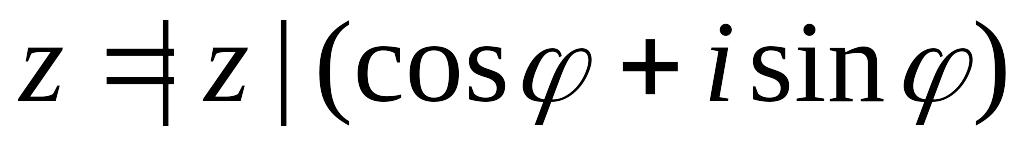 ,
то
,
то
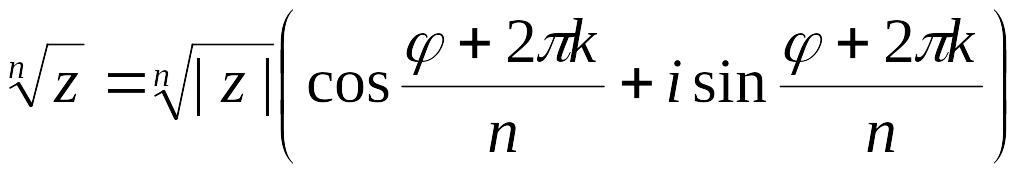 ,
где
,
где
![]() =0,1,…
=0,1,…
![]() ;
;
если , то
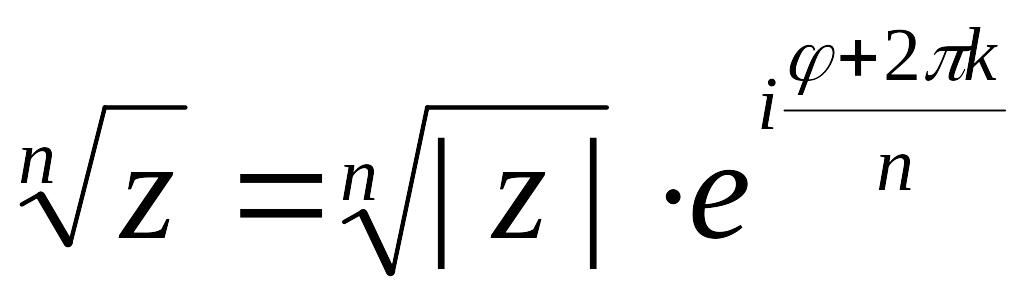 ,
где
=0,1,…
.
,
где
=0,1,…
.
Таблица основных эквивалентностей
1.
|
7.
|
2.
|
8.
|
3.
|
9.
|
4.
|
10.
|
5.
|
11.
|
6.
|
12.
|

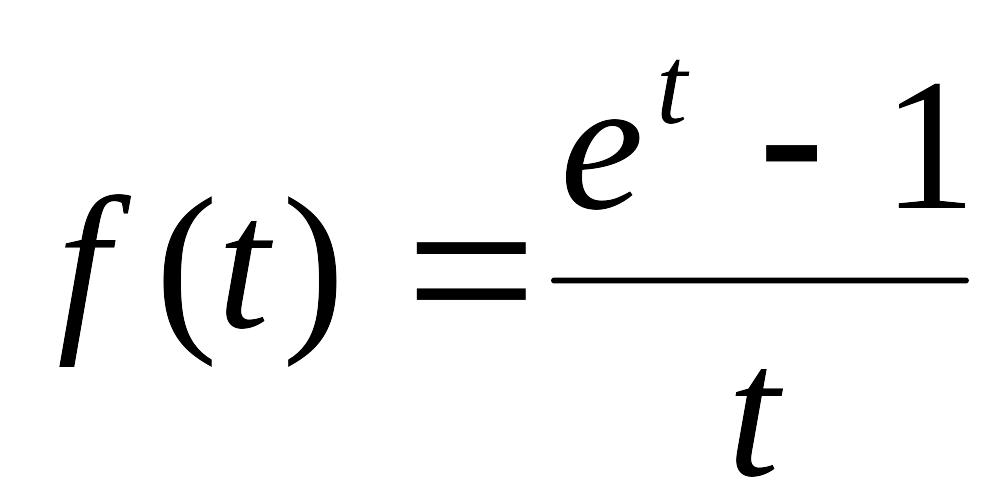 .
.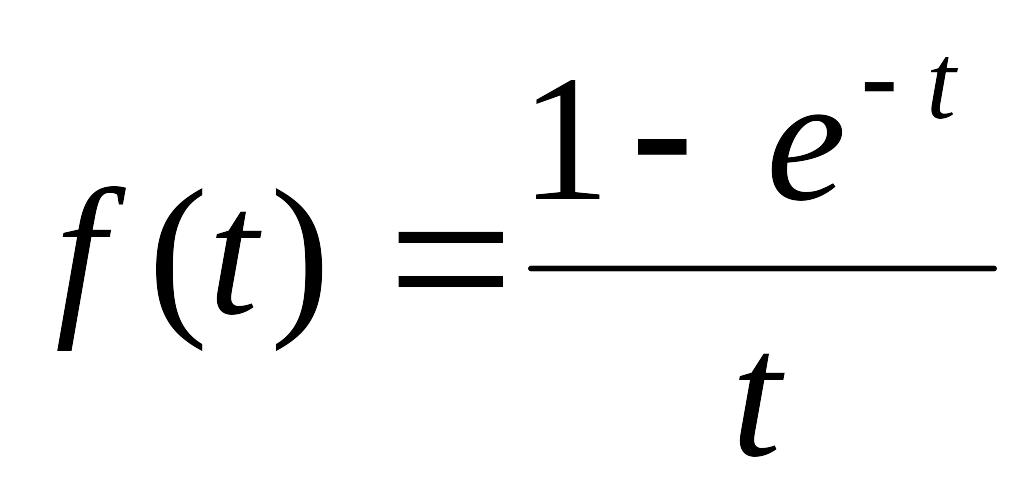 .
.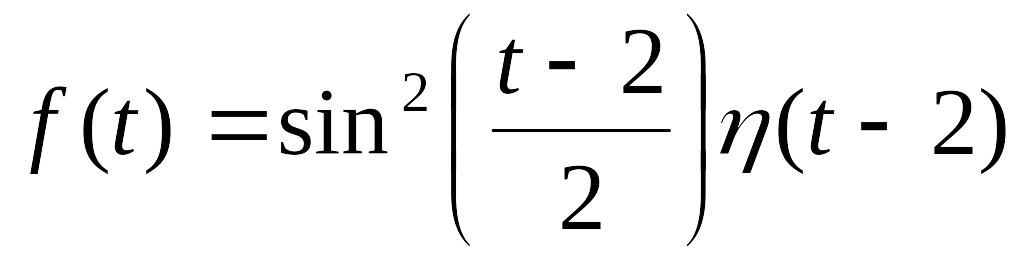 .
.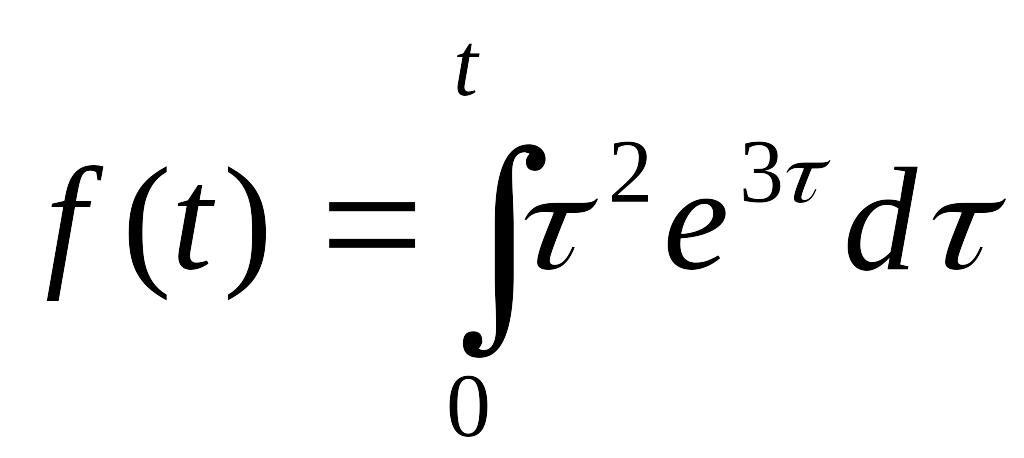 .
.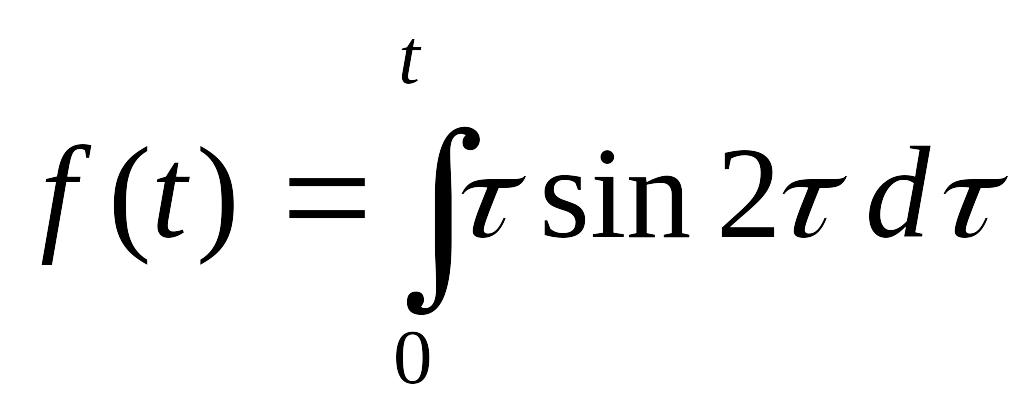 .
.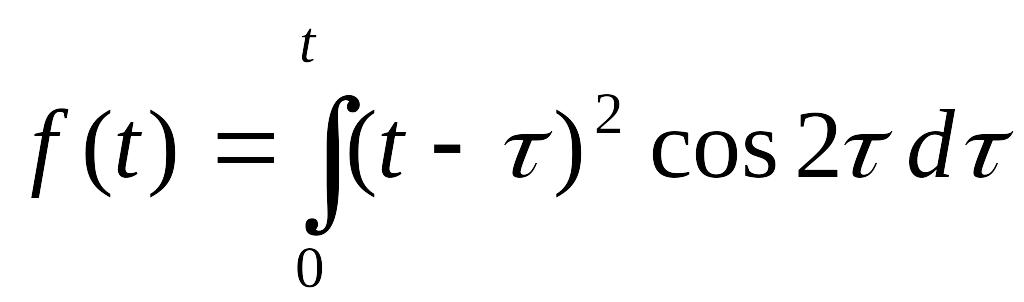 .
.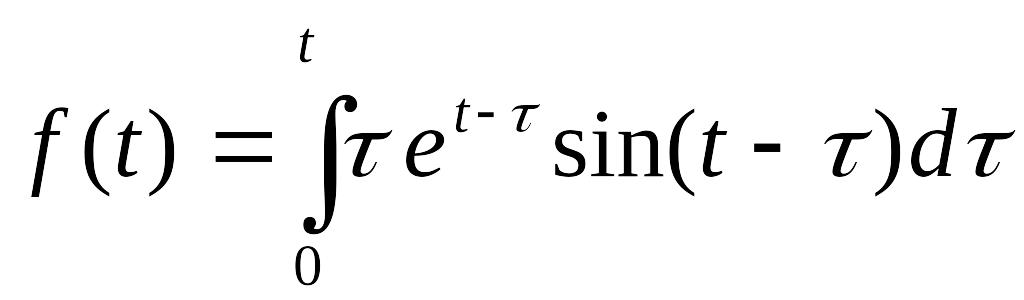 .
. .
.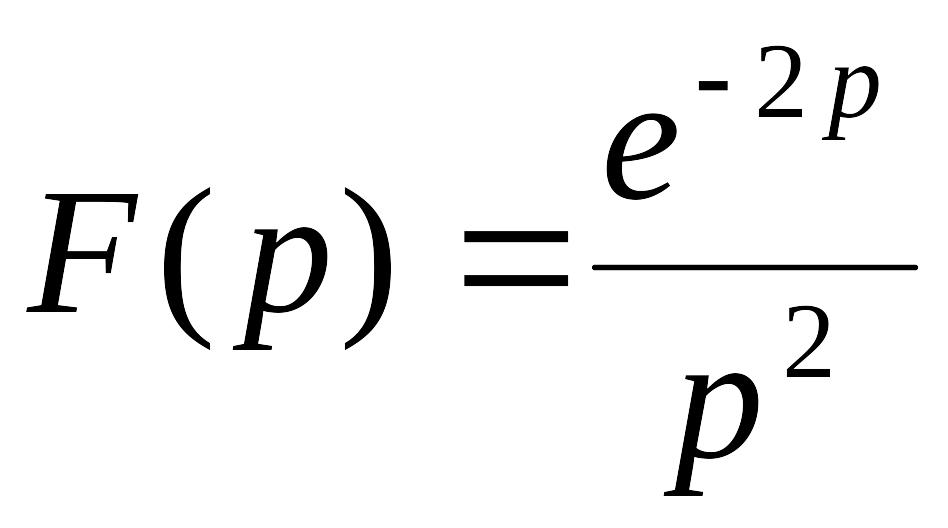 .
.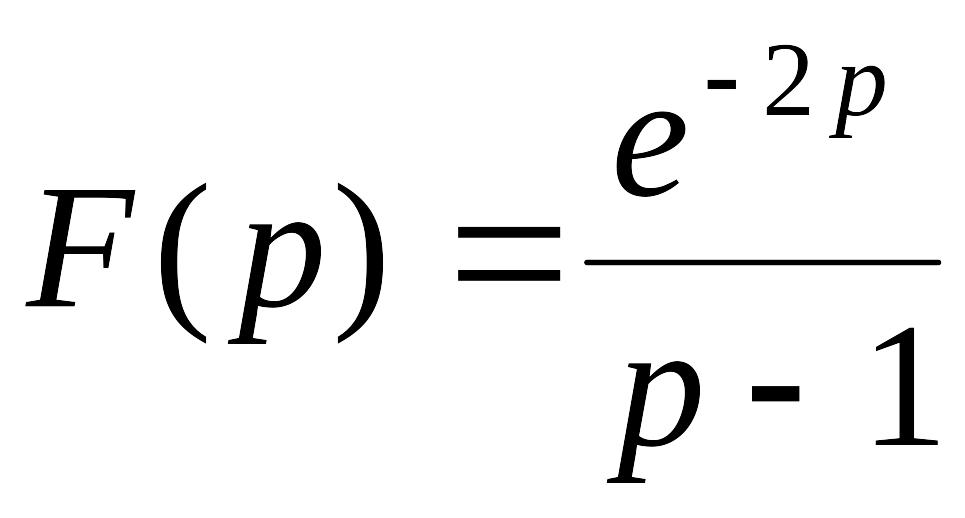 .
.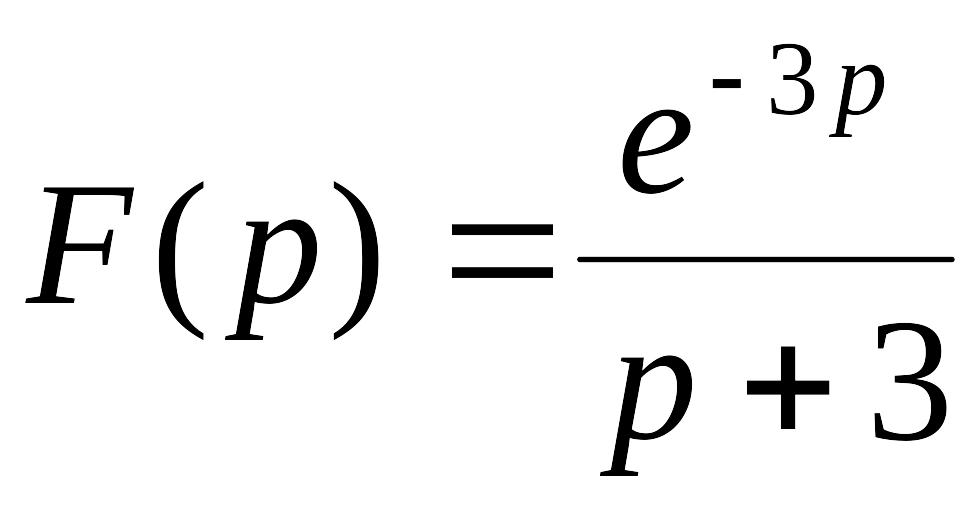 .
.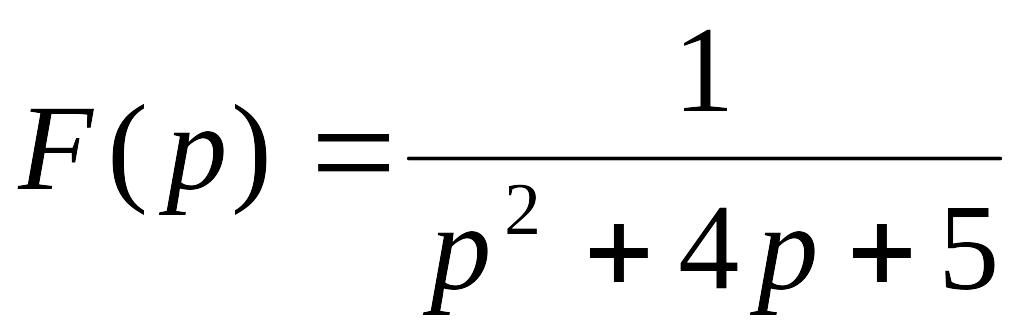 .
.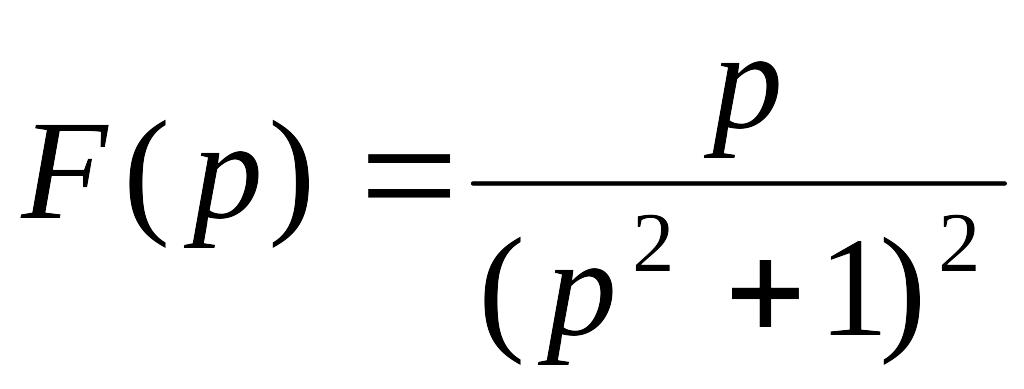 .
.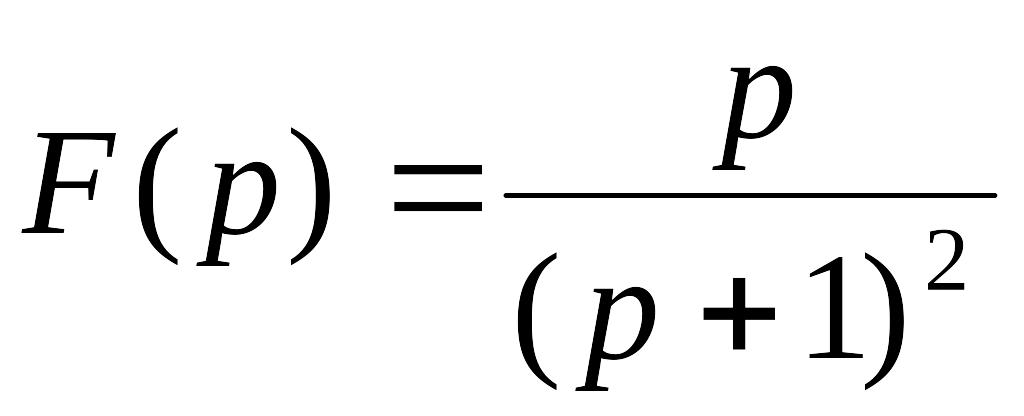 .
.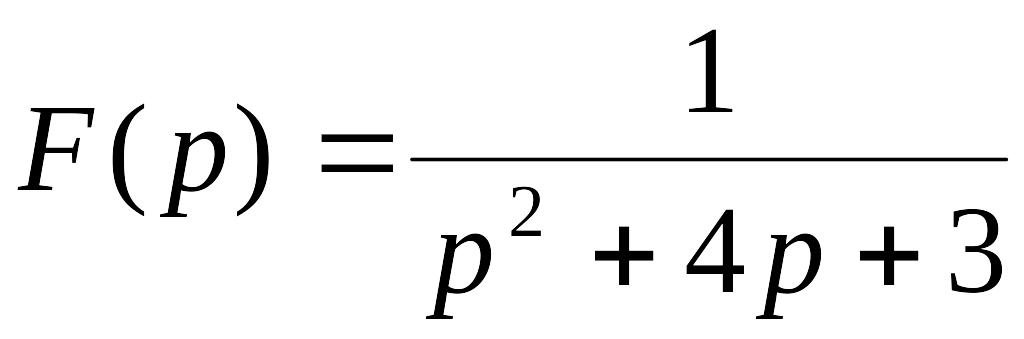 .
.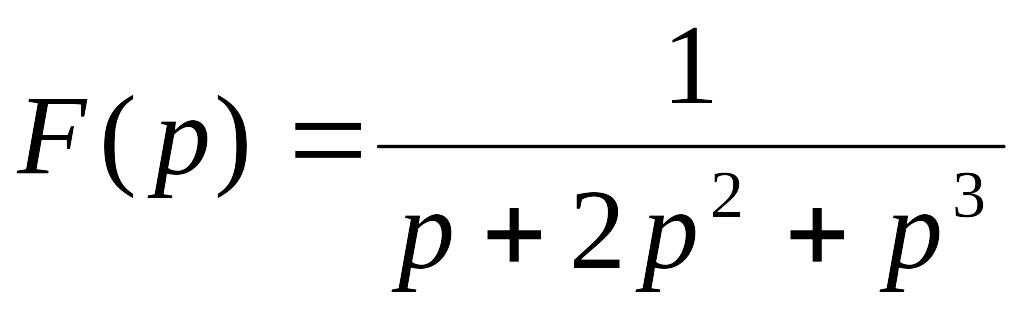 .
.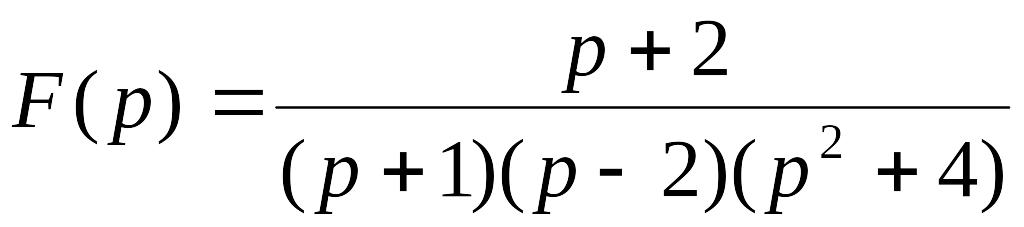 .
.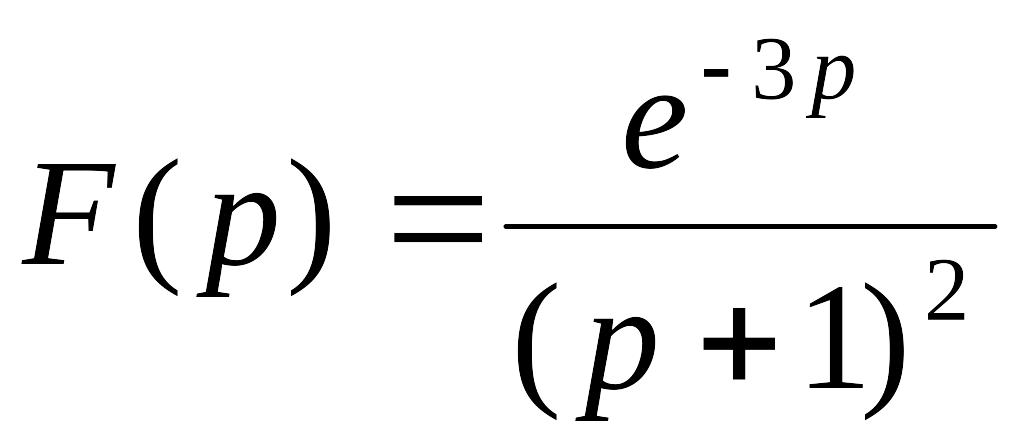 .
.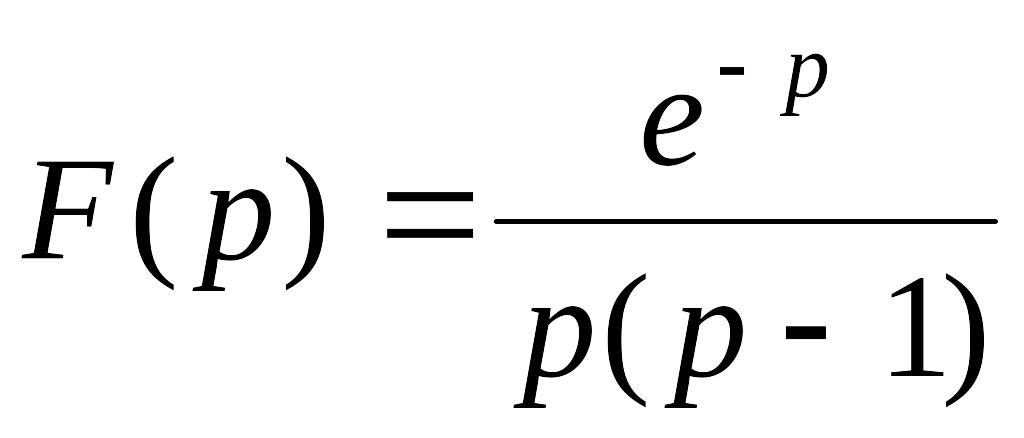 .
.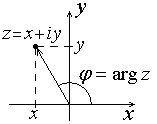

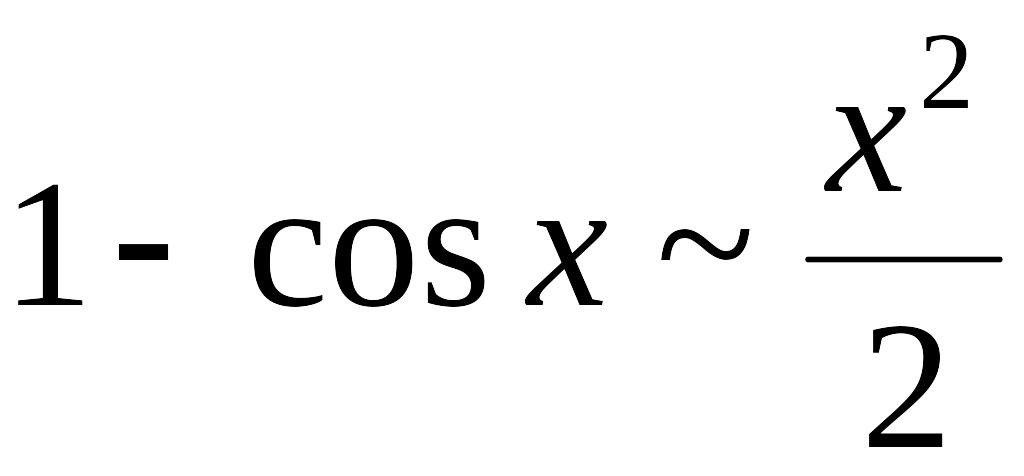 при
при