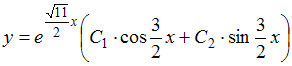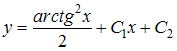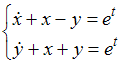- •Тема: Типы дифференциальных уравнений
- •Тема: Поле направлений и изоклины
- •Тема: Дифференциальные уравнения с разделяющимися переменными
- •Тема: Типы дифференциальных уравнений
- •Тема: Поле направлений и изоклины
- •Тема: Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Тема: Типы дифференциальных уравнений
Уравнение
![]() является …
является …
|
|
|
уравнением с разделяющимися переменными |
|
|
|
линейным дифференциальным уравнением 1-го порядка |
|
|
|
однородным относительно x и y дифференциальным уравнением первого порядка |
|
|
|
уравнением Бернулли |
Решение:
Данное
уравнение можно представить в виде
![]() Откуда
Откуда
 Следовательно,
это уравнение является уравнением с
разделяющимися переменными.
Следовательно,
это уравнение является уравнением с
разделяющимися переменными.
![]()
Тема: Поле направлений и изоклины
Дано
дифференциальное уравнение
![]() Тогда
его изоклины представляют собой …
Тогда
его изоклины представляют собой …
|
|
|
семейство окружностей |
|
|
|
пучок прямых, проходящих через одну точку |
|
|
|
семейство гипербол |
|
|
|
семейство параллельных прямых |
Решение:
Данное
уравнение можно представить в виде
 Уравнения
изоклин имеют вид
Уравнения
изоклин имеют вид
 или
или
![]() При
При
![]() эти
уравнения задают семейство окружностей
с центром
в начале координат.
эти
уравнения задают семейство окружностей
с центром
в начале координат.
Тема: Дифференциальные уравнения с разделяющимися переменными
Если угловой коэффициент касательной к кривой в любой ее точке равен удвоенной абсциссе точки касания, то уравнение этой кривой будет иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Угловой
коэффициент касательной в произвольной
точке равен производной в этой точке,
то есть
![]() Тогда
для нахождения уравнения искомой кривой
получим уравнение
Тогда
для нахождения уравнения искомой кривой
получим уравнение
![]() Решив
его, получим
Решив
его, получим
![]()
Тема: Однородные дифференциальные уравнения первого порядка
Общий
интеграл дифференциального уравнения
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Линейные неоднородные дифференциальные уравнения первого порядка
Общее
решение дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Введем
замену
![]()
![]() Тогда
уравнение
примет
вид:
Тогда
уравнение
примет
вид:
![]() или
или
![]() Пусть
Пусть
![]() Тогда
Тогда
![]() Подставим
найденное значение u
в уравнение
Подставим
найденное значение u
в уравнение
![]() .
Получим:
.
Получим:
![]() то
есть
то
есть
![]() и
и
![]() Окончательное
решение имеет вид
Окончательное
решение имеет вид
![]()
Тема: Задача Коши для дифференциального уравнения первого порядка
Решение
задачи Коши
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
![]() перепишем
в виде
перепишем
в виде
![]() Введем
замену
Введем
замену
![]() Получим:
Получим:
![]() или
или
 Пусть
Пусть
![]() Тогда
Тогда
![]() Подставим
найденное значение u
в уравнение
Подставим
найденное значение u
в уравнение
 Получим:
Получим:
![]() То
есть
То
есть
![]() и
и
![]() Тогда
общее решение примет вид
Тогда
общее решение примет вид
![]() Подставим
в найденное общее решение начальное
условие
Подставим
в найденное общее решение начальное
условие
![]() тогда
тогда
![]() и
и
![]() Следовательно,
частное решение имеет вид
Следовательно,
частное решение имеет вид
![]()
Тема: Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общее
решение линейного однородного
дифференциального уравнения второго
порядка
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Составим
характеристическое уравнение
![]() и
решим его:
и
решим его:
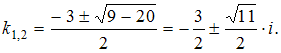 Тогда
общее решение исходного уравнения
примет вид
Тогда
общее решение исходного уравнения
примет вид

Тема: Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий
вид частного решения
![]() линейного
неоднородного дифференциального
уравнения второго порядка
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Общее
решение этого уравнения можно записать
в виде
![]() где
функция
где
функция
![]() –
общее решение однородного уравнения
–
общее решение однородного уравнения
![]() а
функция
а
функция
![]() –
некоторое частное решение исходного
неоднородного уравнения.
Для
однородного уравнения составим
характеристическое уравнение
–
некоторое частное решение исходного
неоднородного уравнения.
Для
однородного уравнения составим
характеристическое уравнение
![]() и
найдем его корни:
и
найдем его корни:
![]() Тогда
общее решение однородного уравнения
будет иметь вид
Тогда
общее решение однородного уравнения
будет иметь вид
![]() Поскольку
правая часть исходного уравнения
Поскольку
правая часть исходного уравнения
![]() то
имеем уравнение со специальной правой
частью. Так как
то
имеем уравнение со специальной правой
частью. Так как
![]() не
является корнем характеристического
уравнения, а
не
является корнем характеристического
уравнения, а
![]() –
является, то частное решение
неоднородного
уравнения будем искать в виде
–
является, то частное решение
неоднородного
уравнения будем искать в виде
![]()
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее
решение дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Проинтегрируем
последовательно обе части уравнения
два раза:
![]()
![]() То
есть общее решение примет вид
То
есть общее решение примет вид
![]()
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Функции
![]() и
и
![]() являются
решением системы дифференциальных
уравнений …
являются
решением системы дифференциальных
уравнений …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Найдем
![]() и
и
![]() :
:
![]()
![]() Подставив
Подставив
![]() в
систему
в
систему
 видим,
что второе уравнение не обращается в
тождество. Подставив
в
систему
видим,
что второе уравнение не обращается в
тождество. Подставив
в
систему
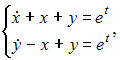 видим,
что первое уравнение не обращается в
тождество. Подставляя
в
систему
видим,
что первое уравнение не обращается в
тождество. Подставляя
в
систему
 получаем,
что оба уравнения не обращаются в
тождество. При подстановке
в
систему
получаем,
что оба уравнения не обращаются в
тождество. При подстановке
в
систему
 оба
уравнения обращаются в тождество.
Следовательно, функции
и
оба
уравнения обращаются в тождество.
Следовательно, функции
и
![]() являются
решением системы дифференциальных
уравнений
являются
решением системы дифференциальных
уравнений