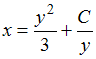Тема: Типы дифференциальных уравнений

Уравнение  является …

			однородным относительно x и y дифференциальным уравнением первого порядка
			линейным дифференциальным уравнением первого порядка
			дифференциальным уравнением с разделяющимися переменными
			уравнением Бернулли

Решение: Уравнение  можно представить в виде   где функция 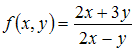 является однородной относительно x и y функцией нулевого порядка. Действительно,   Поэтому данное уравнение является однородным относительно x и y дифференциальным уравнением первого порядка.

Тема: Поле направлений и изоклины

Уравнения семейства изоклин дифференциального уравнения  имеют вид …

Решение: Семейство изоклин дифференциального уравнения  описывается уравнением  где   В рассматриваемом случае получим  Отсюда  или  где  то есть То есть семейство изоклин описывается уравнением

Тема: Дифференциальные уравнения с разделяющимися переменными

Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …

Решение: Угловой коэффициент касательной в произвольной точке равен производной в этой точке, то есть  а угловой коэффициент радиус-вектора точки касания определяется отношением  Тогда для нахождения уравнения искомой кривой получим уравнение с разделяющимися переменными  Разделив переменные, получим 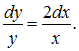 Проинтегрируем обе части этого уравнения: 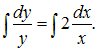  Тогда  где  Откуда  

Тема: Однородные дифференциальные уравнения первого порядка

Дифференциальное уравнение  заменой  приводится к уравнению с разделенными переменными, которое имеет вид …

Решение: Если  то  и Тогда уравнение  запишется в виде Преобразовав уравнение и разделив переменные, получим:

Тема: Линейные неоднородные дифференциальные уравнения первого порядка

Общее решение дифференциального уравнения   имеет вид …

Решение: Примем за неизвестную функцию  Тогда уравнение  можно записать в виде  или  Введем замену    Тогда уравнение 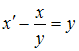 примет вид  или 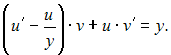Пусть 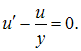 Тогда  Подставим найденное значение u в уравнение  Получим: , то есть  Окончательное решение имеет вид

_______________________________________________________________