Вариант 3

1. Найти сумму, разность, произведение, частное комплексных чисел и , и значение выражения . Результаты вычислений изобразить на комплексной плоскости. , .

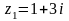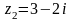2. Найти модуль и аргумент комплексного числа .

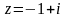3. Найти и изобразить на плоскости множество значений комплексных чисел, удовлетворяющих неравенству 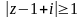, Re z<1, .

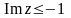4. Представить комплексное число в тригонометрической и показательной форме: .

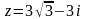5. Найти значение выражения ( )

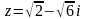   а) k=2

   б) k= 3/5

6. Дано . Тогда

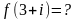
7. Дана функция , где . Тогда

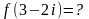
8. Найти действительную и мнимую часть .

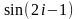9. Пусть 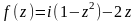, , 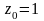тогда ?

10. Заданы уравнения линий, ограничивающих область D. Найти ее образ при дробно-линейном отображении . D: , , .

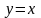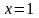11. Найти аналитическую функцию по следующим данным: , .

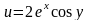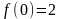12. Вычислить интеграл 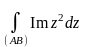, АВ - отрезок прямой , .

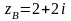13. Разложить функцию в ряд Лорана: , .

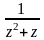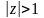14. Найти вычеты функций:

а)

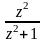
б)

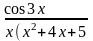
15. Вычислить интеграл с помощью вычетов, найденных в предыдущей задаче:

а)

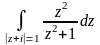
б)

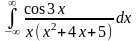
Вариант 4

1. Найти сумму, разность, произведение, частное комплексных чисел и , и значение выражения . Результаты вычислений изобразить на комплексной плоскости. , .

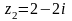2. Найти модуль и аргумент комплексного числа .

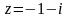3. Найти и изобразить на плоскости множество значений комплексных чисел, удовлетворяющих неравенству , .

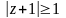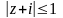4. Представить комплексное число в тригонометрической и показательной форме: .

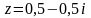5. Найти значение выражения ( )

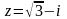   а) k= 3

   б) k= 4/7

6. Дано . Тогда

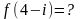
7. Дана функция , где . Тогда

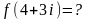
8. Найти действительную и мнимую часть .

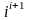9. Пусть 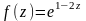, , 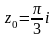тогда ?

10. Заданы уравнения линий, ограничивающих область D. Найти ее образ при дробно-линейном отображении . D: , , .

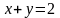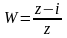
11. Найти аналитическую функцию по следующим данным: , , .

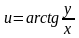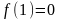12. Вычислить интеграл 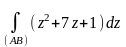, АВ - отрезок прямой , .

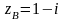13. Разложить функцию в ряд Лорана: , .

14. Найти вычеты функций:

а)

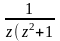
б)

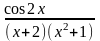
15. Вычислить интеграл с помощью вычетов, найденных в предыдущей задаче:

а)

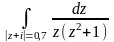
б)

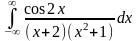
Вариант 5

1. Найти сумму, разность, произведение, частное комплексных чисел и , и значение выражения . Результаты вычислений изобразить на комплексной плоскости. , .

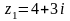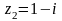2. Найти модуль и аргумент комплексного числа .

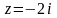3. Найти и изобразить на плоскости множество значений комплексных чисел, удовлетворяющих неравенству , .

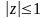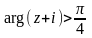4. Представить комплексное число в тригонометрической и показательной форме: .

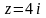5. Найти значение выражения ( )

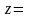   а) k= 5

   б) k= 1/3

6. Дано . Тогда

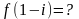
7. Дана функция , где . Тогда

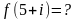
8. Найти действительную и мнимую часть .

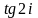9. Пусть 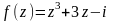, , 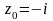тогда ?

10. Заданы уравнения линий, ограничивающих область D. Найти ее образ при дробно-линейном отображении . D: , , , .

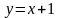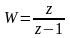
11. Найти аналитическую функцию по следующим данным: .

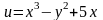12. Вычислить интеграл 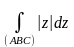, АВС – ломаная , , .

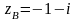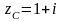13. Разложить функцию в ряд Лорана: , .

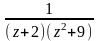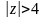14. Найти вычеты функций:

а)

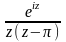
б)

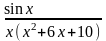
15. Вычислить интеграл с помощью вычетов, найденных в предыдущей задаче:

а)

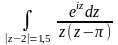
б)