Производная функции комплексного переменного

Если в точке существует предел , то он называется производной функции в точке и обозначается или .

Если в точке функция имеет производную , то говорят, что функция дифференцируема в точке .

Функция , дифференцируемая в каждой точке некоторой области и имеющая в этой области непрерывную производную , называется аналитической в области .

Если функция дифференцируема в точке , то в этой точке существуют частные производные , , , , причем эти производные связаны условиями:

; , (28)

которые называются условиями Коши-Римана.

Условия Коши-Римана являются необходимыми условиями дифференцируемости функции в точке .

Верно и обратное утверждение: если частные производные , , , непрерывны в точке и условия Коши-Римана (28) выполнены, то функция дифференцируема, а следовательно и аналитична, в точке .

Производная функции при выполнении условий (28) может быть записана соответственно:

Производные элементарных функций вычисляются по тем же формулам, что и для действительного аргумента:

Задача 9. Пусть , . Найти .

Решение. Найдем производную, используя формулу для , учитывая, что данная функция является сложной:

.

Тогда

.

Задача 10. Найти аналитическую функцию по следующим данным:

, .

Решение. Т.к. является более сложной функцией, чем , воспользуемся сначала вторым условием Коши-Римана: .

Т.е.

, где - произвольная функция от переменной .

Теперь воспользуемся первым условием Коши-Римана: .

.

.

Приравнивая полученные выражения и , получим

.

Тогда .

Воспользуемся условием: при ( ), получим:

. Тогда .

Конформное отображение

Отображение области , заданное аналитической функцией , называется конформным.

Отображение, осуществляемое линейной функцией _, отображает треугольник в подобный треугольник . Координаты точек и находятся в результате подстановки значений координат точек и в функцию .

П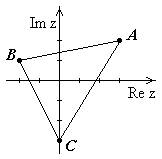 ример. Найти образ треугольника с вершинами в точках и при отображении , если , , .

Решение.

Найдем ,

,

Рис.13

.

И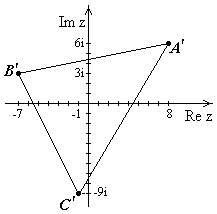 зобразим на координатной плоскости - образ .

Дробно-линейная функция отображает окружность в окружность (прямая линия считается окружностью бесконечного радиуса).

Рис.14

Замечание: Две произвольные линии, пересекающиеся в точке , отображаются в две соответствующие линии, пересекающиеся в точке так, что угол между касательными к исходным и отображенным линиям один и тот же.

Задача 11. Заданы уравнения линий, отображающих область . Найти ее образ при дробно-линейном отображении .

Р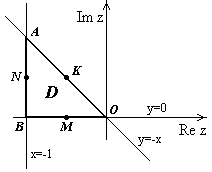 ешение: Построим область : . Из рисунка видно, что - треугольник . Найдем

образы точек при заданном отображении: .

Рис.15

, ,

Рис.15

,

,

.

Т.к. отображение дробно-линейное, то окружность отображается в окружность.

Возьмем дополнительные точки области - середины отрезков , , : , , .

, , .

.

Отрезок отображается в дугу .

, .

О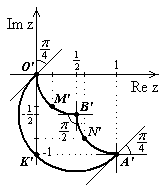 трезок отображается в дугу .

Рис.16

.

Проверим свойства сохранения углов:

, (углы между касательными к дугам и , и )и т.д.

Область - образ области при заданном отображении .

Замечание: Если в результате отображения некоторая точка отображается в

, то считаем, что - все точки окружности с радиусом .

Пусть - произвольная гладкая кривая, лежащая в области , - функция комплексного переменного, непрерывная в области . Тогда по определению

, ( -маленькая) если предел в правой части существует и не зависит ни от способа разбиения дуги на частичные дуги точками , ни от выбора точек .

Если функция -аналитическая функция в области , то значение интеграла не зависит от линии , а зависит от значений начальной и конечной точек этой линии и . Тогда , где -первообразная функции . Т.е. для вычисления интеграла от аналитической функции применяют обычные формулы интегрирования и формулу Ньютона-Лейбница.

Теорема Коши. Если -аналитическая функция в области , то интеграл , взятый по любому замкнутому контуру , равен нулю.

Если не является аналитической функцией, причем , то вычисление интеграла сводится к вычислению двух криволинейных интегралов второго рода:

. (29)

З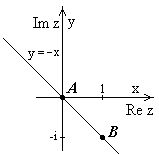 адача 12.1. , .

Рис.17

Решение. Функция является аналитической. Тогда можно воспользоваться формулой Ньютона-Лейбница, учитывая, что интеграл не зависит от пути интегрирования, а зависит только от начальной и конечной точек.

.

Задача 12.2. , .

Р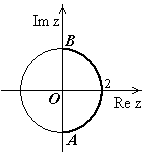 ешение. Функция - не является аналитической, значит требуется вычисление при помощи криволинейных интегралов. Путь интегрирования на чертеже: - окружность с центром в т. и радиусом 2; -берем только правую половину окружности. .

Найдем действительную и мнимую часть функции :

Рис.18

.

,

т.к. , где ; .

Тогда , т.е.