
- •Основы теории функции комплексной переменной
- •Алгебраические операции над комплексными числами
- •Тригонометрическая форма комплексного числа
- •Произведение комплексных чисел, заданных в тригонометрической форме
- •Формула Эйлера
- •Понятие функции комплексного переменного
- •Основные элементарные функции комплексной переменной.
- •Производная функции комплексного переменного
- •Конформное отображение
- •Ряды Лорана
- •Вычеты функции
- •Применение вычетов к вычислению интегралов.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Решение типового варианта
- •Список литературы
Понятие функции комплексного переменного
Если
каждому комплексному числу
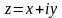 поставлено в соответствие некоторое
комплексное число
поставлено в соответствие некоторое
комплексное число
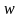 ,
то говорят, что в области
,
то говорят, что в области
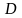 определена комплексная функция
определена комплексная функция
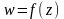 .
.
Задача
6.
Дано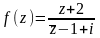 .
Найти
.
Найти
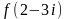 .
.
Решение.
Подставим в заданную функцию
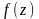 значения:
значения: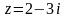 ,
,
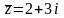 .
.
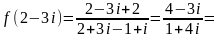
(домножим числитель и знаменатель на число, сопряженное знаменателю)
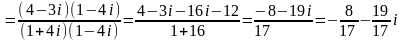 .
.
Задача
7.
Дана функция
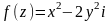 ,
где
,
где
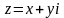 .
Тогда
.
Тогда
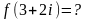
Решение.
По условию
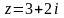
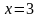 - действительная часть числа
,
- действительная часть числа
,
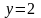 - мнимая часть.
- мнимая часть.
Тогда
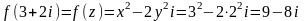 .
.
Пусть
,
а
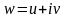 .
Тогда функция
может быть представлена с помощью двух
действительных функций
.
Тогда функция
может быть представлена с помощью двух
действительных функций
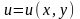 и
и
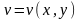 ,
зависящих от действительных переменных
и
,
зависящих от действительных переменных
и
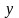 :
:
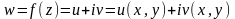 ,
,
где
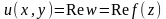 - действительная часть функции
,
- действительная часть функции
,
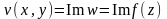 -
мнимая часть функции
.
-
мнимая часть функции
.
Задача
8. Найти
действительную и мнимую часть функции
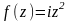 .
.
Решение. , тогда
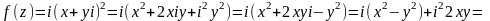
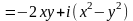 .
.
Таким
образом
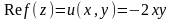 ,
,
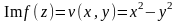 .
.
Основные элементарные функции комплексной переменной.
Показательная функция.
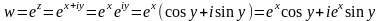 .
(15)
.
(15)
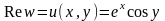 ,
,
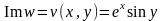 .
.
Пример.
Найти
действительную и мнимую части числа
 .
.
Решение.
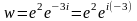
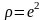 ,
,
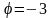 (в радианах).
(в радианах).
Запишем в тригонометрической форме:
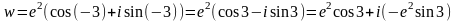 ,
,
(напомним,
что
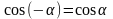 ,
,
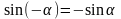 )
)
Тогда
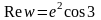 ,
,
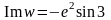 .
.
Тригонометрические функции.
Используя
разложение в ряд Тейлора функций
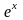 ,
,
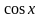 ,
,
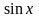 ,
найдем разложение следующих функций:
,
найдем разложение следующих функций:
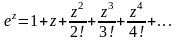 (16)
(16)
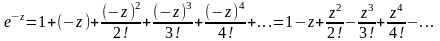 (17)
(17)
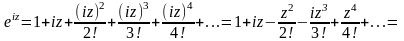
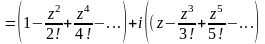 (18)
(18)
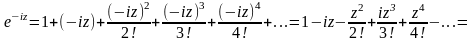
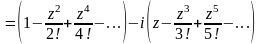 (19)
(19)
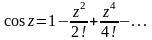 (20)
(20)
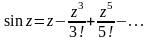 (21)
(21)
Заметим,
что
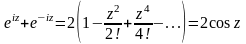
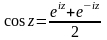 (22)
(22)
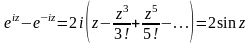 ,
,
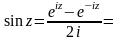
(домножим
числитель и знаменатель на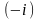 )
)
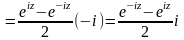 (23)
(23)
Тогда
можно вывести формулы
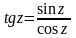 и
и
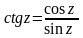 .
.
Пример.
Найти
действительную и мнимую часть числа
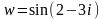 .
.
Решение. Воспользуемся формулами:
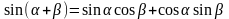 ,
,
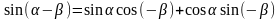 .
.
Тогда:
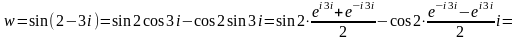
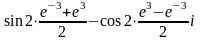 .
.
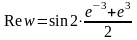 ,
,
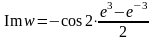 .
.
Гиперболические функции.
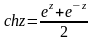 ;
;
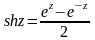 ;
;
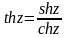 ;
;
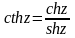 .
(24)
.
(24)
Логарифмическая функция.
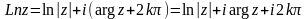 (25)
(25)
Выражение
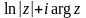 называется
главным значением логарифмической
функции и обозначается
называется
главным значением логарифмической
функции и обозначается
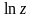 .
Таким образом,
.
Таким образом,
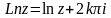 .
(26)
.
(26)
Видно,
что функция
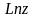 имеет множество значений, отличающихся
друг от друга на
имеет множество значений, отличающихся
друг от друга на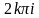 .
.
Пример.
Найти
действительную и мнимую часть числа
 .
.
Решение.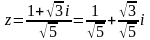 ,
т.е.
,
т.е.
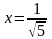 ,
,
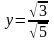 .
.
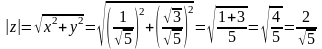 .
.
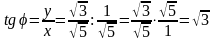 .
.
Т.к.
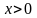 и
и
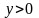 лежит в первом квадранте, т.е.
лежит в первом квадранте, т.е.
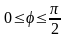 .
.
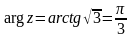
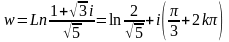
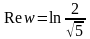 ;
;
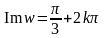 .
.
Общая степенная
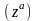 и общая показательная
и общая показательная
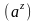 функции:
функции:
а) ,
б)
,
б)
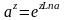 .
(27)
.
(27)
Обе
функции имеют множество значений,
поскольку в формулу их вычисления
входит функция
или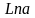 ,
которая сама по себе имеет множество
значений.
,
которая сама по себе имеет множество
значений.
Аналогично
определяется
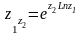 .
.
Пример.
Найти действительную и мнимую часть
числа
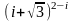 .
.
Решение.
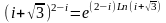 .
.
Преобразуем
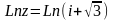 ;
;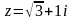 ,
,
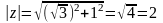 ,
,
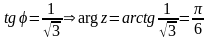 ,
,
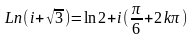 .
.
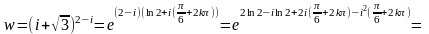
=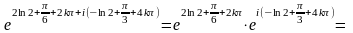
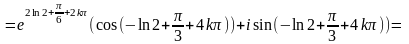
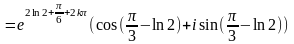 .
.
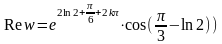 ,
,
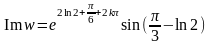 .
.
