Вариант 30

1. Найти сумму, разность, произведение, частное комплексных чисел и , и значение выражения . Результаты вычислений изобразить на комплексной плоскости. , .

2. Найти модуль и аргумент комплексного числа .

3. Найти и изобразить на плоскости множество значений комплексных чисел, удовлетворяющих неравенству .

4. Представить комплексное число в тригонометрической и показательной форме: .

5. Найти значение выражения ( )

   а) k= 3

   б) k= 4/5

6. Дано . Тогда

7. Дана функция , где . Тогда

8. Найти действительную и мнимую часть .

9. Пусть , , тогда ?

10. Заданы уравнения линий, ограничивающих область D. Найти ее образ при дробно-линейном отображении . D: , , , .

11. Найти аналитическую функцию по следующим данным: .

12. Интеграл от комплексной функции на отрезке прямой АВ равен?

13. Разложить функцию в ряд Лорана: .

14. Найти вычеты функций:

а)

б)

15. Вычислить интеграл с помощью вычетов, найденных в предыдущей задаче:

а)

б)

Решение типового варианта

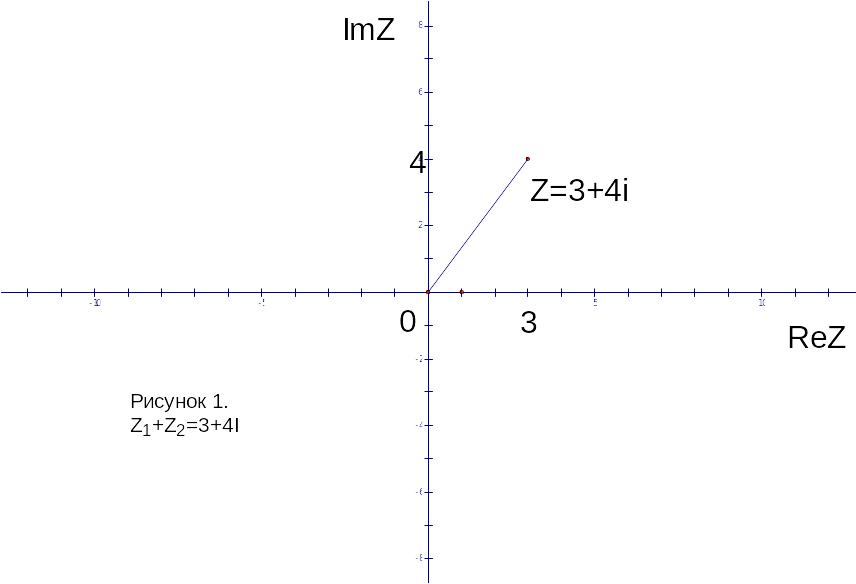
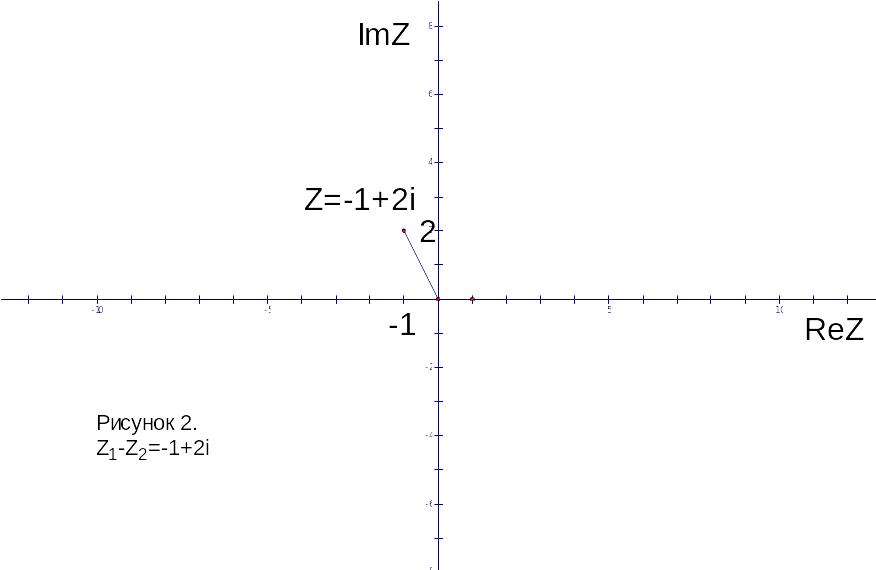
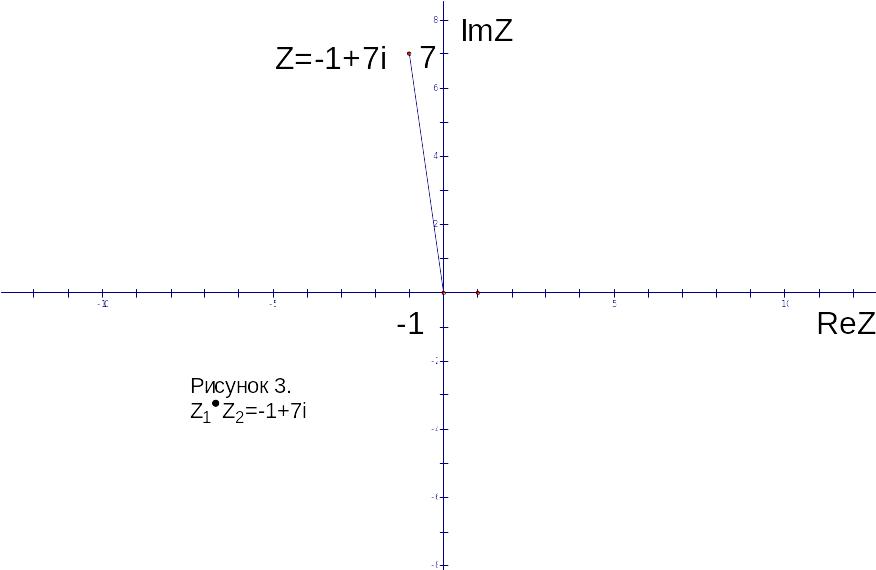
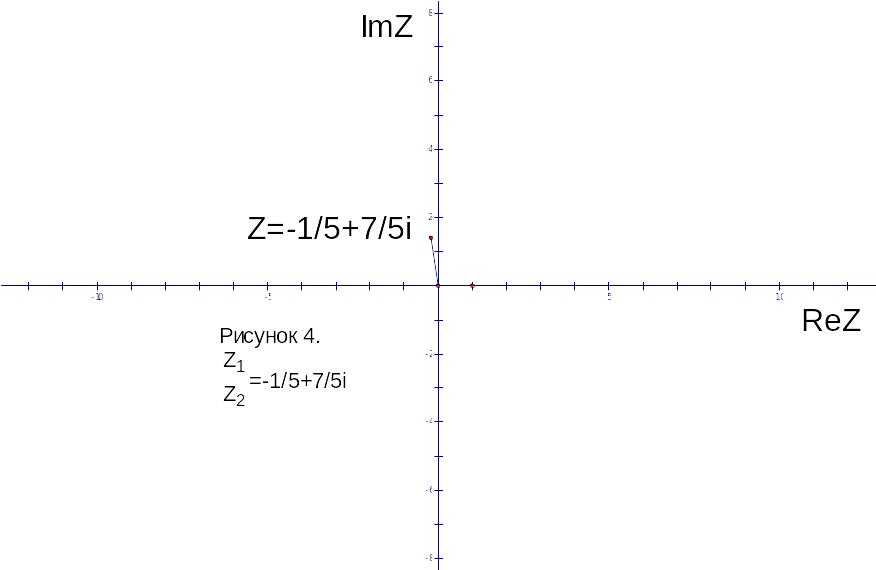
Задача №1. Найти сумму, разность, произведение, частное комплексных чисел и и значение выражения . Результаты вычислений изобразить на комплексной плоскости. , .

Решение.

Напомним необходимые формулы и понятия.

Числа и называются комплексно – сопряженными

Сложение и вычитание комплексных чисел производится по правилам сложения и вычитания векторов, но умножение и деление комплексных чисел не имеют непосредственных аналогов в векторной алгебре.

Запишем

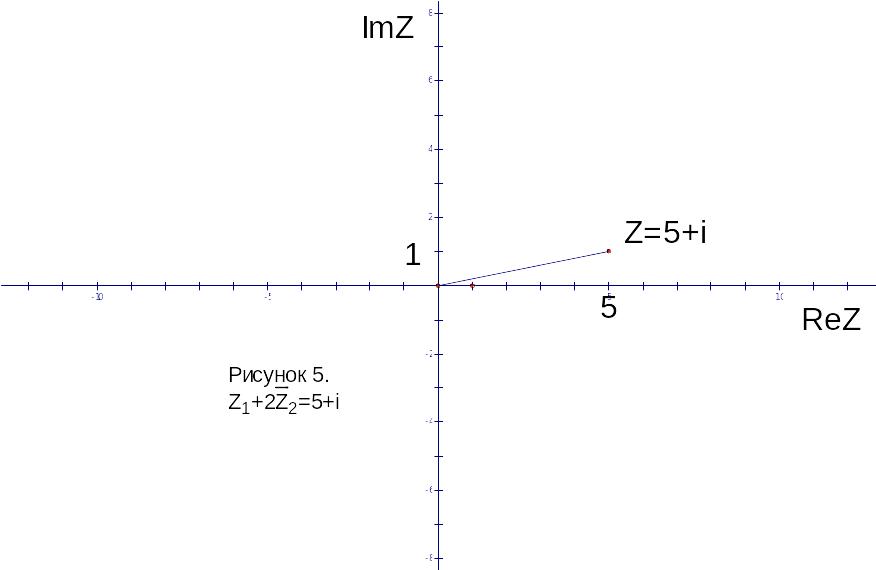
Задача №2. Найти модуль и аргумент комплексного числа .

Решение.

Модуль числа определяется по формуле и равен ,

главное значение аргумента .

Аргумент комплексного числа можно вычислить из формулы

Задача №3. Представить комплексное число в тригонометрической и показательной форме: .

Решение.

Модуль числа определяется по формуле и равен

Главное значение аргумента .

Комплексное число в тригонометрической форме:

Комплексное число в показательной форме:

Запишем комплексное число в алгебраической, тригонометрической и показательной формах:

Задача №4. Найти действительную и мнимую часть .

Решение.

Задача №5. Найти значение выражения ( ), если а) k= 3, б) k=1/3

Решение.

Число представим в тригонометрическом виде , где

Тогда .

Воспользуемся формулой Муавра:

Найдем

Для этого применим формулу:

Задача №6. Найти и изобразить на плоскости множество значений комплексных чисел, удовлетворяющих условию

Решение.

- модуль разности двух комплексных чисел равен расстоянию между точками, изображающими эти числа на плоскости.

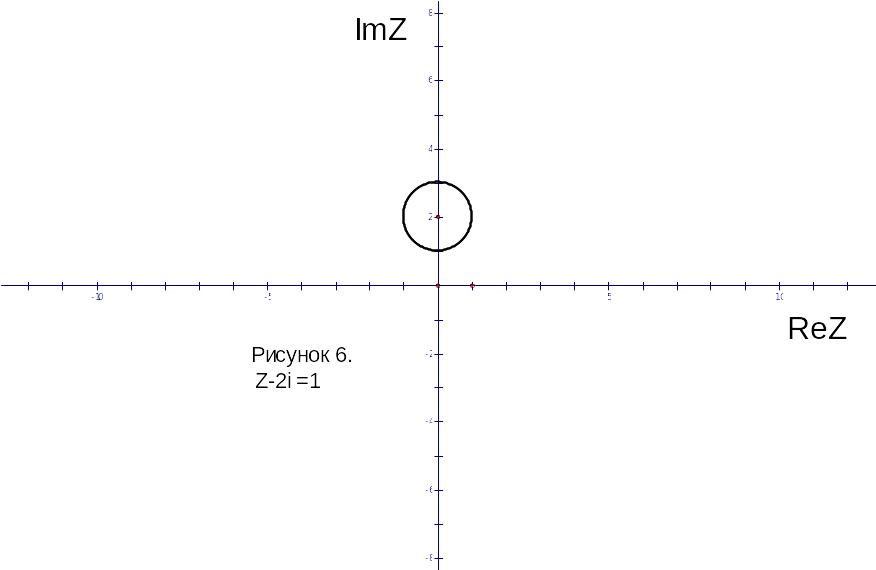
Равенство определяет на комплексной плоскости множество точек , находящихся на расстоянии от точки , т.е. окружность с центром в точке и радиусом .

Задача №7. Дано . Тогда

Решение.

По условию задачи имеем . Подставим в функцию:

Напомним, что

Задача №8. Дана функция , где . Тогда

_{Решение.}

Имеем , т.е. Получаем при подстановке

Задача №9. Пусть , ,тогда ?

Решение.

Вычислим производную функции . Подставим значение . Получим:

Задача №10. Найти образ области D, ограниченной линиями , , , при дробно-линейном преобразовании .

Решение.

Графическое изображение области D представляет собой пространство внутри треугольника ABC:

Рисунок 7 – Область D

Каждая точка на плоскости R² отождествляется с комплексным числом:

, , , .

Преобразование , действуя на область D, каждой точке этой области поставит в соответствие точку из C. Найдем образы вершин треугольника ABC относительно W:

, , , .

Поэтому:

, , , .

Рассмотрим также образы точек E и F – середин отрезков BC и OC соответственно:

, .

Поскольку при рассматриваемом конформном отображении прямые, проходящие через вершины A и C, B и C переходят в прямые, а отрезок AB в дугу окружности, то, учитывая сохранение углов области D, получим образ D относительно преобразования W:

Рисунок 8 – Образ области D при преобразовании W

Задача №11. Восстановить аналитическую функцию по заданной действительной части при условии .

Решение.

Из условий О. Коши–Б. Римана: ,

Откуда .

Теперь из условия , получим ^.

Отсюда и . Для отыскания значения постоянной C воспользуемся условием ; имеем

, .

Окончательно, запишем

Задача №12. Вычислить интеграл , АВ – отрезок прямой, соединяющий точки , .

Решение.

1 способ.

Если то интеграл сводится к двум криволинейным интегралам от действительных функций по формуле:

Имеем т.е.

2 способ.

Задача №13. Разложить функцию в ряд Лорана: , .

Решение.

Разложим функцию на простейшие дроби:

Приравняем числители: . Полагая , получаем

Отсюда . Полагая , получаем

Таким образом,

_{Учитывая, что} , можно записать:

Следовательно,

Задача №14. Найти вычеты функций:

а)

б)

Решение.

а) Так как то Точки являются полюсами. Применяя формулу для вычисления вычетов:

, получаем:

б)

Введем функцию комплексной переменной

Находим особые точки функции

как нули (1-го порядка) ее знаменателя: и . Таким образом, точки и ─ полюса 1-го порядка. В верхней полуплоскости лежит единственная точка .

Вычисляем вычет в простом полюсе по формуле

где и .

Получаем:

Задача №15. Вычислить интеграл с помощью вычетов, найденных в предыдущей задаче:

а)

б)

Решение.

а) Полюсы находятся внутри замкнутого контура .

Применяя основную теорему о вычетах: , получаем:

б)

Воспользуемся формулой

Несобственный интеграл при помощи вычета равен:

Используя формулу, вычисляем искомый интеграл: