Министерство образования и науки

Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Алтайский государственный технический университет

им. И.И.Ползунова»

И.В.Лощина, Е.В.Мартынова

Основы теории функции комплексной переменной

Методические указания и варианты заданий

для самостоятельной работы студентов технических и

экономических специальностей по курсу математики

Изд-во АлтГТУ

Барнаул 2013

УДК 517.53/.55(075,5)

Лощина И.В., Мартынова Е.В..Основы теории функции комплексной переменной: Методические указания и варианты заданий для самостоятельной работы студентов технических и экономических специальностей по курсу математики/ И.В.Лощина, Е.В.Мартынова; Алт.гос.техн. ун-т им. И.И.Ползунова. –Барнаул: Изд-во АлтГТУ, 2013. – с.

Пособие содержит теоретические сведения и набор задач для индивидуальных заданий по теме: основы теории функций комплексной переменной.

Замечание: нумерация примеров в теоретической части совпадает с нумерацией в индивидуальных заданиях.

Рассмотрено и одобрено на заседании кафедры

«Высшей математики и математического моделирования»

Протокол №7 от 6.03.2013

Рецензент: Половникова Е.С. – к.ф.-м.н.

Известно, что на множестве действительных чисел квадратное уравнение 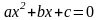имеет действительные корни, если дискриминант больше или равен 0

( ).

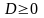Для нахождения корней уравнения с отрицательным дискриминантом было введено понятие 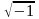, которое называют мнимой единицей и по предложению Леонарда Эйлера обозначают буквой 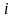(от латинского «imaginarium» – «мнимый»). Тогда .

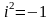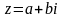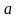Число , где и 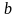- действительные числа, называется комплексным числом, причем называется действительной частью числа 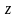, а - его мнимой частью. Обозначают: , .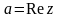

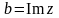Геометрически любое действительное число можно представить точкой на числовой оси (рис.1):

Рис.1

Рис.2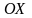

По предложению Гаусса в начале 19 века комплексные числа можно представить в виде точек на плоскости, где ось - действительная ось, а ось 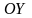- мнимая ось (рис.2).

Алгебраические операции над комплексными числами

Алгебраические операции над комплексными числами выполняются как над многочленами:

1. Сумма комплексных чисел:

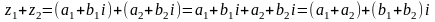₍₁₎

2. Разность комплексных чисел:

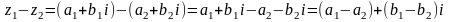(2)

3. Произведение комплексных чисел:

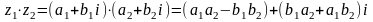
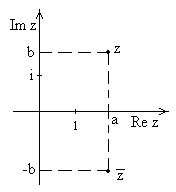(3)

Числа и 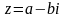называются сопряженными комплексными числами. При изображении этих чисел на комплексной плоскости видно, что они симметричны относительно действительной оси (рис.3).

Найдем значение выражения 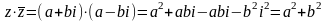, т.к. . Получено действительное число.

Рис.3

4. Деление комплексных чисел:

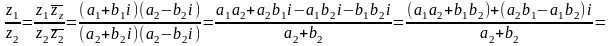
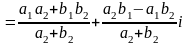(4)

В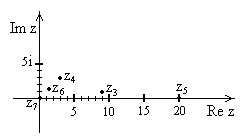 идно, что сумма, разность, произведение и частное комплексных чисел также являются комплексными числами.

Задача 1.Даны числа 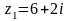, 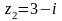. Найти:

Рис.4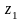

1) сумму, разность, произведение, частное чисел и ,

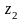2) значение выражения .

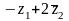Решение. 1а) ;

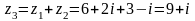1б) ;

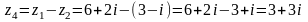1в) ;

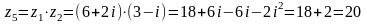1д) ;

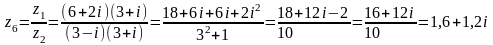2) (рис.4).