§4.9. Нормальное отражение плоской ударной волны от абсолютно жесткой стенки

Пусть на бесконечную абсолютно жесткую стенку падает по нормали к её поверхности плоская ударная волна, рис. 33“а”

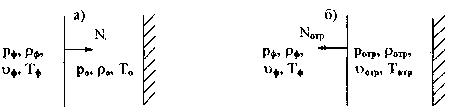
Рис.33. Отражение плоской ударной волны от жесткой стенки

Параметры невозмущенной среды на этом рисунке обозначены через p₀, ₀, Т₀, и ₀, параметры среды за фоном ударной волны через р_ф, _ф, _ф, Т_ф; скорость перемещения фронта N.

В момент встречи ударной волны со стенкой возникает отраженная волна, распространяющаяся в обратном направлении со скоростью N_отр, рис.33”б”. Её параметры обозначены через р_отр, _отр, _отр, Т_отр.

Нормальная составляющая скорости частиц на стенке по условиям задачи равна нулю.

Согласно формуле (4.50), для скорости воздуха в ударной волне имеет место соотношение

_,

где V₀=1/₀, V_ф=1/_ф

_{Аналогично}

_(4.85)

Принимая во внимание, что на стенке_отр -_ф = 0, нетрудно получить

или

_(4.86)

Соотношение (4,86) может быть преобразовано к виду

(4.87)

Согласно (4.54) выполняются соотношения:

_и

Исключая с помощью этих соотношений величины _отр и _ф из (4.87), можно получить [4]

_(4.88)

Формула (4.88) носит название формулы Измайлова (более строго Измайлова-Крюссара). Она может быть приведена к виду

(4.89)

Или, что то же

_(4.90)

Из формул (4.89), (4.90) следует, что для ударной волны малой амплитуды ( )

Таким образом, давление на преграде удваивается по сравнению с давлением за фронтом прямой волны, что совпадает с известным результатом отражения акустических волн.

В другом предельном случае, когда , при k=1,4

Используя соотношения (4.50), можно найти остальные гидродинамические элементы волн у стенки, а именно:

_(4.91)

Представляет интерес сопоставления давления отражения при падении ударной волны на жесткую стенку, определяемого формулой (4.90), с давлением заторможенного потока, рассчитываемого по интегралу Бернулли (4.18)

Подставив в данное выражение значения скорости газа , скорости звука из (4.54), заменив давление P на P_ф, можно получить

(4.92)

Формула (4.92) получена Ю.Б. Харитоном [4].

Если рассматривается падение ударной волны не на жёсткую стенку, а преграду конечных размеров типа промышленного или жилого здания, то после прохождения ударной волны здания, сооружения и окончания дифракционных процессов устанавливается режим обтекания.

Силовое воздействие на преграду в режиме установившегося обтекания определяется зависимостью

_{, (4.93)}

где, c_x – коэффициент лобового сопротивления рассматриваемого объекта;

s – площадь его поперечного сечения.

Подставляя в данное соотношение значения ,  из (4.54), можно получить

_{, (4.94)}

Значения коэффициента c_x обычно находятся экспериментально при продувках в аэродинамических трубах.

На рис.34 приведено сопоставление величин давления отражения ∆Р_отр=Р_отр–Р_о, давления в заторможенном потоке ∆Р_*=Р_*–Р_о и давления в установившемся режиме обтекания для прямоугольной пластины, расположенной по нормали к направлению потока при ∆Р_ф400 кПа.

Рис.34. Давление отражения и скоростного напора в сопоставлении с давлением в заторможенном потоке

1 – давление отражения,

2 – давление в заторможенном потоке,

3 – давление скоростного напора

Из рисунка видно, что отношение ∆Р_*/∆Р_отр 1/2. Данный результат играет важную роль при оценке внешних сил, возникающих на преграде при воздействии воздушной ударной волны.