
- •1. Навчальна програма з теорії ймовірності
- •1.1. Основні поняття та формули теорії ймовірності
- •1.2. Схема повторних незалежних випробувань Бернуллі
- •1.3. Випадкові величини
- •1.4. Числові характеристики випадкових величин та їх властивості
- •2.2. Приклад розв’язку задачі з теорії ймовірності
- •3. Основні означення, закони, формули і приклади розв’язків задач з
- •3.1. Події, класифікація та операції над ними.
- •3.2. Елементи комбінаторики
- •Залежні та незалежні події.
- •3.5. Формули повної ймовірності та Байєса.
- •3.6. Формула Бернуллі.
- •3.7. Наближені формули обчислення ймовірностей.
- •3.8. Дискретні випадкові величини.
- •3.9. Неперервні випадкові величини.
- •3.10. Операції над випадковими величинами.
- •3.11. Числові характеристики випадкових величин.
- •3.12. Двовимірні випадкові величини.
- •3.13. Нерівність Чебишева, теорема Чебишева та Бернуллі.
- •3.14. Випадкові процеси. Марковські процеси.
Залежні та незалежні події.
Дві події А і В будемо називати незалежними, якщо ймовірність появи однієї з них не залежить від появи чи непояви іншої.
У протилежному випадку вони називатимуться залежними.
Умовною ймовірністю рА(В) називають ймовірність події В, обчислену за умови того, що подія А вже наступила.
рА(В) = р(А В)/р(А). (11)
Згідно з (11) отримаємо для ймовірності добутку залежних подій:
р(А В)=р(А)∙рА(В) (12)
або
р(А В)=р(В) ∙рВ(А). (13)
Формула добутку для n залежних подій А1,...,Аn матиме вигляд:
р(А1 ... Аn ) =р(Аn)∙ рAn(А1 ... Аn-1). (14)
Формула (14) методом математичної індукції може бути розписана на ймовірності окремих подій. Наприклад, для трьох залежних подій
А1,А2,А3: р(А1 А2 А3) = р(Аз) ∙рА3(А2)∙рА2 А3(А1).
Якщо події А і В незалежні, то умовна ймовірність стає «безумовною»:
рВ(А) = р(А).
У випадку коли події А і В незалежні, то формули (12-14) мають
простіший вигляд, а саме: р(А В) = р(А)∙р(В) (15)
або р(А1 ... Аn ) = р(А1)∙...∙р(Аn), (16)
для попарно незалежних подій.
Випробування називаються незалежними, якщо їхні наслідки незалежні в сукупності.
Формула для обчислення ймовірності появи принаймні однієї з n незалежних випадкових подій А, має вигляд:
р(С) = 1 – q1q2 … qn. (17)
ІІриклад 9. В урні є 3 білі і 3 чорні кульки. 3 неї два рази виймають навмання по одній кульці, не повертаючи їх назад. Знайти імовірність витягування спочатку білої, а потім чорної кульок.
• Позначимо через А подію, що буде витягнута біла кулька, а
В— чорна. Оскільки витягування спочатку білої, а потім чорної
кульок є перетин С = А В, то за формулою (13)
Р(А В) = Р(А)∙РА(В).
За класичним означенням ймовірності Р(А) = 3/6 = 1/2. Після першого випробування в урні залишилось 5 кульок, з них, згідно з
умовою задачі, 2 білі і 3 чорні. Тому за формулою (4) РА(В) = 3/5.
Звідси Р(А В) = 0,5 • (3/5) = 0,3. •
Приклад 10.
Ймовірність появи деякої випадкової події у першому випробуванні дорівнює 0,9 у другому — 0,8, у третьому — 0,7. Яка ймовірність того, що при трьох випробуваннях подія з'явиться принаймні один раз?
• Позначимо появу події в і-му випробуванні Аі.
За умовою задачі р(А1) = р1 = 0,9; р(А2) = р2 = 0,8; р(Аз) = р3 = 0,7.
Тоді q1 = 0,1; q2 = 0,2; q3 = 0,3. Використаємо формулу (17):
р(С) = 1 - 0,1 • 0,2 • 0,3 = 1 - 0,006 = 0,994. •
3.5. Формули повної ймовірності та Байєса.
Формула
повної ймовірності р(А) =
![]() ,
(18)
,
(18)
Випадкові події Н1,Н2, …, Нn , називаються гіпотезами.
Для переоцінки ймовірностей гіпотез Ні, за умови, що подія А з'явилася,
тобто для обчислення ймовірностей р(Ні/А) користуються формулою
Байєса:
р(Ні/А)
=
 =
=
![]() (19)
(19)
Приклад 11. Вивчаються результати екзамену з математики у
двох групах. У першій групі є 28 студентів, з них 10 отримали відмінну оцінку, а в другій відповідно — 22 і 7. Яка ймовірність, що навмання вибраний студент отримав на екзамені відмінну оцінку?
• Випробування полягає в тому, що ми навмання вибираємо
одного студента з двох груп.
Позначимо через А подію, що навмання вибраний студент на екзамені з математики отримав відмінну оцінку. Це може статися, коли студента вибрано з першої групи (відбулася подія Н1) або — другої (Н2).
За статистичним означенням ймовірності
р(Н1)= 28/50; р(Н2) = 22/50.
Використаємо формулу повної ймовірності
р(А) = р(Н1)·р(А/Н1) + р(Н2)·р(А/Н2).
За умовою задачі р(А/Н1) = 10/28, р(А/Н2)= 7/22.
Звідси
р(А)
=
![]() =
=
![]() .
.
Приклад 12. У першому ящику маємо 8 стандартних і 2 браковані деталі, а у другому — 5 стандартних і 5 бракованих. Ящики мають однаковий зовнішній вигляд. З навмання вибраного ящика взято (також навмання) дві деталі, які виявилися стандартними. Яка ймовірність того, що їх взяли з другого ящика?
• Позначимо через А подію, що вибрано дві стандартні деталі,
через Н1 — що навмання взяті дві деталі були взяті з першого ящика,
Н2 - що навмання взяті дві деталі були взяті з другого ящика. Обчислимо ймовірність цих подій до проведення спроби:
р(Н1)
=
![]() ; р(А/Н1)
=
; р(А/Н1)
=
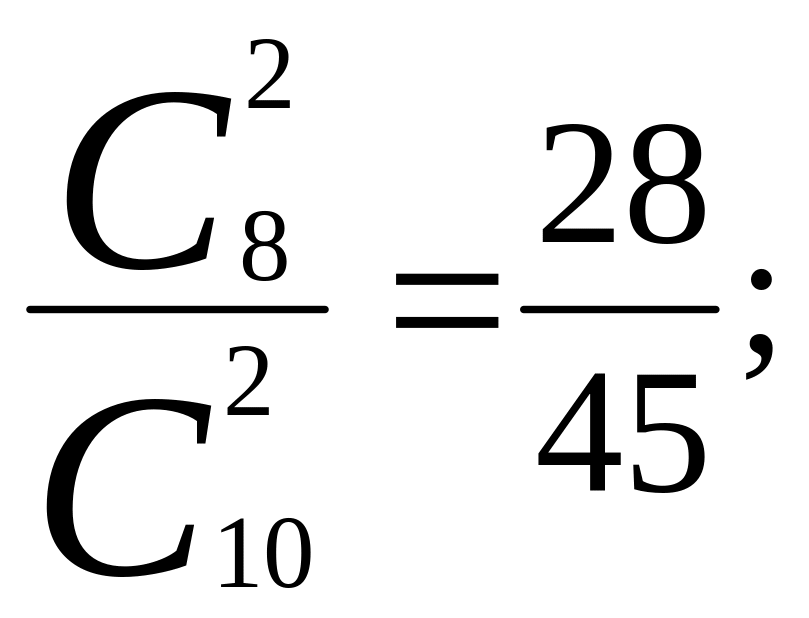
р(Н2)
=
![]() ; р(А/Н2)
=
; р(А/Н2)
=

Для переоцінки ймовірностей гіпотези Н2 використаємо формулу Байєса
р(Н2/А)
=
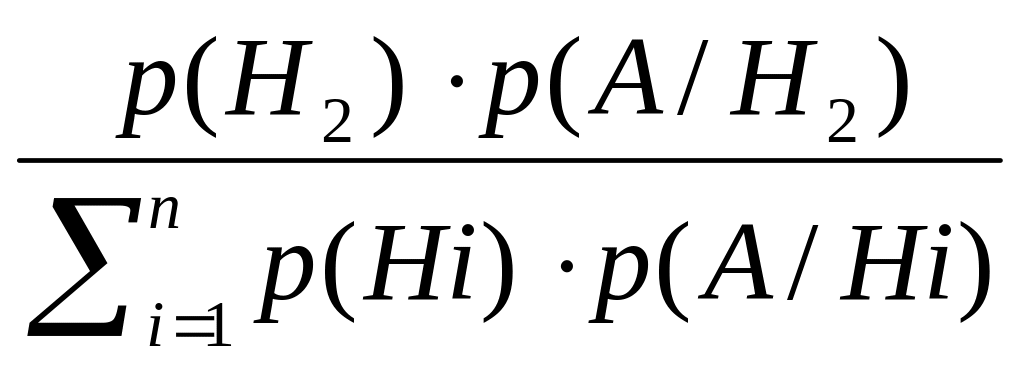 =
=
 =
=
![]() •
•
