3.2. Елементи комбінаторики

Перестановкою з n різних елементів називається об'єкт, який

складається з n цих елементів, і відрізняється від інших місцем розташування.

Кількість перестановок позначають символом Р_n і розраховують за формулою: Рn =n!. (1)

Розміщенням з n елементів по к називають об'єкт, що складається з к елементів, вибраних з n і розташованих у певному порядку.

Два розміщення, що складаються з однакових елементів, але відрізняються місцем їх розташування, вважаються різними.

Число розміщень з n елементів по k будемо позначати символом A .

Має місце формула для підрахунку числа розміщень:

A = n(n-1)...[(n- k+1)], (2)

Комбінацією з n елементів по k будемо називати такі розміщення з n елементів по k, які відрізняються хоча б одним елементом.

Зауважимо, що комбінації, які відрізняються лише місцем

розташування елементів, вважаються однаковими: {1; 2} і {2; 1}.

Позначимо число комбінацій з n елементів по k символом С .

Для обчислення числа комбінацій використовується формула

С = або С = . (3)

Число комбінацій позначають також символом Ньютона:

(читають «число комбінацій з n по k).

Приклад 2.

Скількома способами можна посадити за одним столом 5 студентів?

Наслідок 1. Якщо події А і В протилежні, то

р(В) = 1 - р(А), або р( ) = 1 - р(А). (5)

Наслідок 2. Якщо події Е₁ і Е₂ є несумісними, то

р(Е₁ Е₂) = р(Е₁) + р(Е₂). (6)

Формула (6) може бути узагальнена на довільне число взаємовиключаючих одна одну подій Е₁, ... , Е_k.

р(Е₁ Е₂ Е_k) = р(Е₁) + р(Е₂) + ... + р(Е_k). (7)

Геометрична ймовірність - ймовірність попадання точки в задану область (відрізок, частину площини, тощо), яка має вигляд:

Р(А)=S(А)/S(U), (8)

де S(U) - площа універсальної множини U , а S(А) - площа підмножини А.

Якщо події А і В є сумісними, то справедлива формула

р(А В) = р(А) + р(В) – р(А В). (9)

Відносною частотою події називають відношення числа випробовувань, в яких подія з'явилась, до загального числа проведених випробовувань.

Формулою це записується так :

w(А) = m/n, (10)

де m — число випробувань, в яких подія А спостерігалася,

n - загальне число випробовувань,

m також називають частотою появи події А.

Статистичною ймовірністю події А будемо називати відносну

частоту появи події А або число, достатньо близьке до неї.

Приклад 5. Набираючи номер телефону, абонент забув одну

цифру і набрав її навмання. Знайти ймовірність того, що набрана цифра — правильна.

• Випробування в даній задачі полягає в тому, що ми навмання

набираємо одну цифру з 10. Позначимо через А подію набору

потрібної цифри і використаємо формулу р(А) = m/n.

Множина елементарних подій U складається з подій, що

набрано цифри 0, 1,..., 9. m( ) = 10, m = 1 (потрібна цифра лише одна). Р(А)=0,1.

Приклад 6. Президент фірми хоче створити команду дизайнерів

для розробки нової моделі товару у складі трьох інженерів і двох спе-

ціалістів з дослідження ринку. Яка ймовірність, що команда такого

складу буде створена, якщо з групи 10 інженерів і 5 спеціалістів з

проблем ринку вибирати навмання п'ять осіб?

• Випробування полягає в тому, що президент вибирає п'ять чоловік. Позначимо через А подію, що навмання відібрана команда з 5 осіб складається з трьох інженерів і двох спеціалістів з проблем ринку.

Шукану ймовірність будемо обчислювати за формулою (4).

У нашому випадку число всіх елементарних подій збігається з числом комбінацій по 5 елементів з 15. n = C = = 3003.

Визначимо число сприятливих подій. Три інженери можна взяти

довільним способом із наявних десяти. Число таких підгруп у групі з

5 чоловік буде збігатися з числом комбінацій з 10 елементів по 3. Останні дві особи повинні бути спеціалістами з ринку. Їх можна взяти С способами.

Вибір інженерів і спеціалістів по ринку здійснюється незалежно:

m = C ∙ С = = 1200.

Шукана ймовірність буде обчислюватись як відношення m/n:

р(А) =

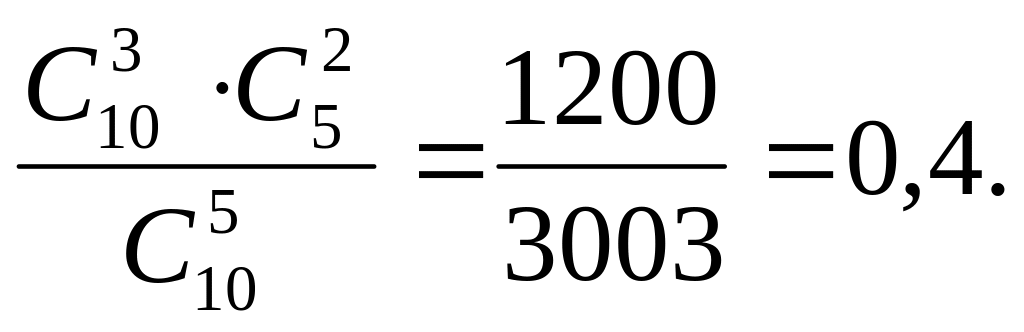
Приклад 7. Задача вибору.

Інвестиційна компанія АBС має k пакетів акцій, серед яких є r пакетів цукрових заводів. Визначити ймовірність того, що серед навмання вибраних m пакетів акції є рівно l пакетів цукрових заводів.

• Оскільки випробування полягає в тому, що ми k пакетів ак-

цій навмання вибираємо m, то це можна зробити С способами.

Сприятлива подія (серед навмання взятих m пакетів акцій є l пакетів

цукрових заводів) може бути реалізована С ∙С способами.

Дійсно, з r пакетів акцій цукрових заводів вибирається рівно l, способів буде С . Інші пакети, а їх буде m - l будуть вибиратися з k - r, тобто їх буде С . Звідси р = С ∙ С : С .

Приклад 8. Дана множина U = {0 ≤ х ≤ 1; 0 ≤ у ≤ 1 }. Яка ймовірність, того, що навмання взята точка з координатами (х, у) буде знаходитися в області А, обмеженою кривими у = х² і у = х ?

• Обчислимо площу фігури А за допомогою означеного інтегралу

у
1
	1		х

S(А) = (кв. од), р(А) = 1/6.