5. Расчет ширины спектра сигнала

Под шириной спектра понимают эффективную область частот, в пределах которой сосредоточена основная энергия сигнала.

Для ограничения спектра сигнала необходимо задаться пороговым критерием. Из рисунка 1.5 видно, что наибольшей энергией обладает первая гармоника, поэтому пороговый критерий для нахождения ширины спектра сигнала определим как десятую часть амплитуды первой гармоники.

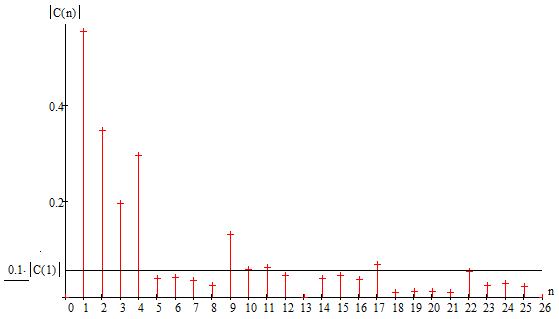
Рисунок 1.8 – Спектр амплитуд коэффициентов комплексного ряда Фурье с пороговым критерием

Прямая линия (рисунка 1.8), параллельная частотной оси, определяется пороговым критерием. Нетрудно заметить, что семнадцатый коэффициент – это последний коэффициент с амплитудой, превышающей порог. Следовала бы ширину спектра брать по восемнадцати гармоническим колебаниям, но, посмотрев на график и проверив по таблице 1, мы обнаружим, что двадцать второй коэффициент меньше пороговой критерии всего на 0,0013. С целью не потерять значимую часть энергии сигнала, восстановление сигнала произведем по двадцати шести гармоническим колебаниям, т. е. взяв лепесток, содержащий двадцать второй коэффициент.

.

6. Восстановление сигнала усеченным рядом фурье

Сигнал, представленный усеченным рядом Фурье, называется оценкой . Учитывая нормировку , оценка опишется следующим рядом:

.

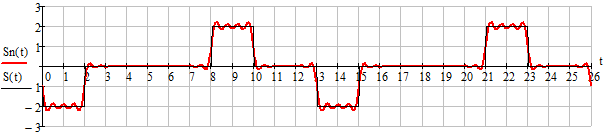
Рисунок 1.9 – Восстановление сигнала усеченным рядом Фурье по 26 гармоническим колебаниям

Восстановленный сигнал имеет периодический, пульсирующий характер. Периодизация сигнала произошла из-за дискретизации спектральной плотности в частотной области, а пульсирует восстановленный сигнал из-за ограниченной двадцатью шестью гармониками ширины спектра сигнала.

Рисунок 1.10 – Восстановление сигнала усеченным рядом Фурье по 100 гармоническим колебаниям

Из рисунков 1.9 и 1.10 видно, что при увеличении числа гармоник восстановленный сигнал становится все более похожим на исходный, т. е уменьшается «завал» переднего и заднего фронта.

7. Расчет и построение погрешности представления аналогового периодического сигнала усеченным рядом фурье

Относительное значение погрешности аппроксимации аналогового периодического сигнала усечённым рядом Фурье определяется как:

,

где – средняя мощность сигнала, – мощность оценки .

Средняя мощность сигнала равна отношению энергии периодического сигнала к периоду:

.

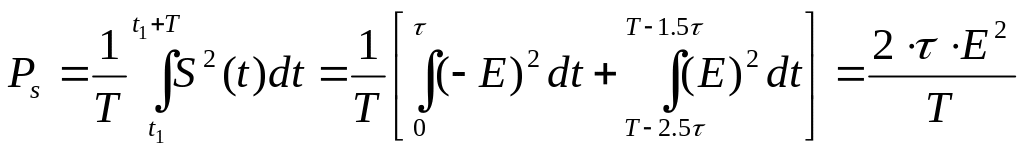Мощность оценки можно определить по спектру как сумму мощностей отдельных гармонических составляющих:

.

Среднеквадратическая погрешность представления аналогового периодического сигнала усечённым рядом Фурье равна:

.

Найдем среднюю мощность погрешности аппроксимации :

ВТ.

Построим погрешность:

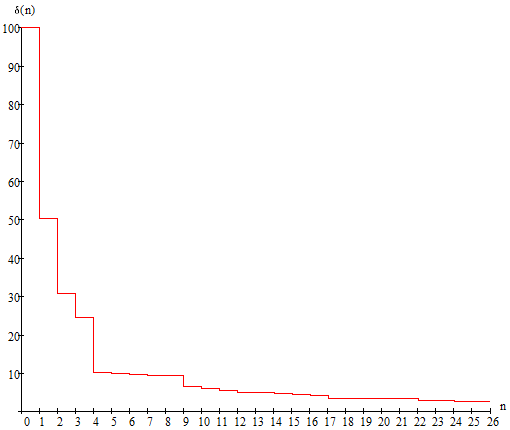
Рисунок 1.11 – Погрешность представления аналогового периодического сигнала усечённым рядом Фурье

Как мы можем видеть, с увеличением числа гармонических колебаний погрешность уменьшается. Если устремить число гармонических колебаний к бесконечности, то погрешность будет стремиться к нулю.

2. Анализ аналоговой линейной электрической цепи

1. Исходные данные

Табличное представление исходных данных:

№ варианта	№ бригады	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	№схемы
09	3	R	2pL	R	R	2pL	R	R	R	3

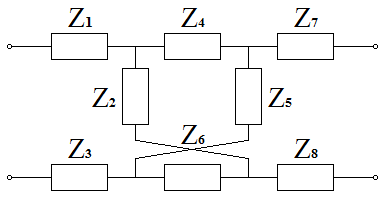
Рисунок 2.1 – Схема исходного аналогового фильтра-прототипа

Известно соотношение постоянной времени цепи: .