7. Проводники в электростатическом поле. Электроемкость проводника

К проводникам относятся вещества, в которых имеются свободные электрические заряды. Для проводников, находящихся в электростатическом поле, выполняются следующие условия:

а) всюду внутри проводника напряжённость поля , а у его поверхности , т.е. вектор напряженности перпендикулярен поверхности проводника;

б) весь объём проводника эквипотенциален;

в) поверхность проводника является эквипотенциальной поверхностью;

г) некомпенсированные (сторонние) заряды располагаются в проводнике только на его внешней поверхности.

Напряжённость и электрическое смещение электростатического поля вблизи поверхности проводника связаны с поверхностной плотностью  зарядов на проводнике:

D_n= _стор., _стор.,

где   относительная диэлектрическая проницаемость окружающей среды.

При сообщении проводнику электрического заряда изменяется и его потенциал. Заряд проводника в однородной и изотропной диэлектрической среде пропорционален его потенциалу:

q = C.

Электрической ёмкостью (электроёмкостью, ёмкостью) называется скалярная физическая величина, численно равная заряду, который нужно сообщить проводнику, чтобы его потенциал стал равен единице:

C = q /.

Электрическая ёмкость уединённого проводящего шара (или сферы) радиусом R рассчитывается по формуле

С = 4₀R,

где   диэлектрическая проницаемость окружающей среды.

8. Взаимная ёмкость. Конденсаторы

Взаимная ёмкость двух проводников численно равна заряду, который нужно перенести с одного проводника на другой для изменения разности потенциалов между ними на единицу:

C = q /(₁-₂).

Ёмкость плоского конденсатора

,

где S  площадь обкладок; d  расстояние между обкладками;   относительная диэлектрическая проницаемость диэлектрика между обкладками.

Ёмкость сферического конденсатора

,

где R₁ и R₂  внутренний и внешний радиусы конденсатора.

Ёмкость цилиндрического конденсатора

.

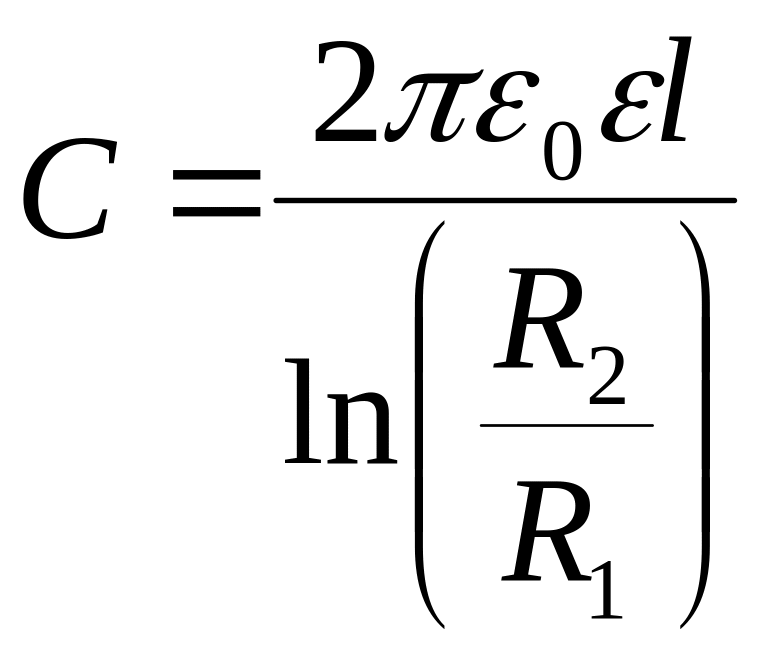Ёмкость батареи параллельно соединённых конденсаторов

.

Ёмкость батареи последовательно соединённых конденсаторов

.

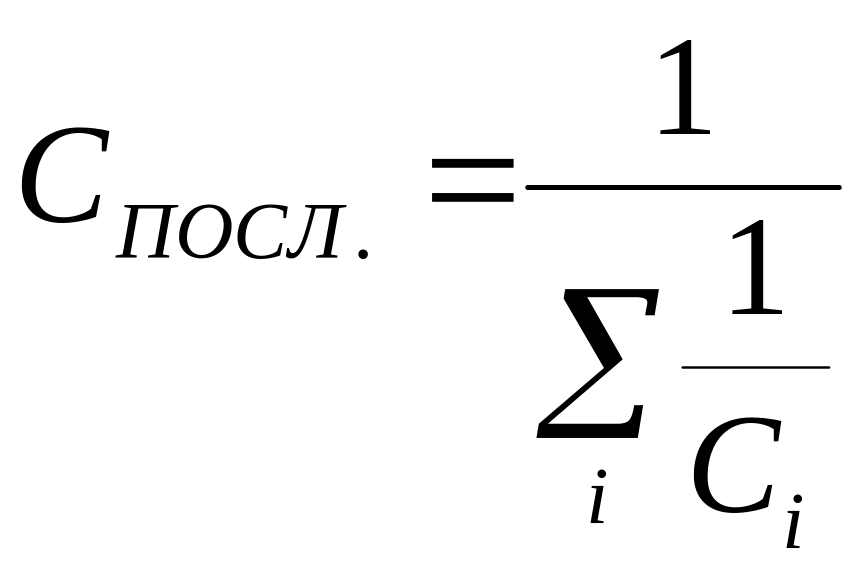9. Потенциальная энергия системы точечных зарядов. Энергия заряженного проводника и электрического поля

Электрические заряды вследствие электрического взаимодействия обладают взаимной потенциальной энергией. Для двух точечных зарядов энергия

.

Для системы точечных электрических зарядов потенциальная энергия

,

где  _i  потенциал электрического поля, создаваемый всеми зарядами системы за исключением i-го, в точке, где находится i-й заряд.

Потенциальная энергия взаимодействия зарядов может быть как положительной, так и отрицательной.

Собственная энергия заряженного уединённого проводника

.

Собственная энергия заряженного конденсатора

.

Собственная энергия заряженного проводника или конденсатора всегда положительная, т.к. она численно равна работе внешних сил по образованию заряда q из бесконечно малых одноименных порций заряда dq.

Распределение энергии поля в пространстве характеризуется объёмной плотностью энергии электростатического поля

.

Энергия электростатического поля, заключенная в объеме V:

.