5. Электрическое поле в диэлектрических средах. Дипольные моменты молекул диэлектрика. Поляризация диэлектрика

Вещества, которые не проводят электрический ток, называются диэлектриками. В диэлектриках, в отличие от проводников, нет свободных носителей заряда. Все молекулы диэлектрика электрически нейтральны. Тем не менее, молекулы обладают электрическими свойствами. В первом приближении молекулу можно рассматривать как электрический диполь с дипольным электрическим моментом .

Как всякий электрический диполь молекула создаёт электрическое поле, поэтому электрические поля диполей, складываясь, создают некоторое собственное поле , которое, налагаясь на внешнее поле , образует результирующее электрическое поле в диэлектрике .

Существуют два основных вида однородных и изотропных диэлектриков:

1) неполярные диэлектрики (атомы и молекулы таких диэлектриков в отсутствие внешнего электрического поля не имеют дипольных моментов, а при помещении в электрическое поле приобретают индуцированные дипольные моменты, пропорциональные величине напряженности поля);

2) полярные диэлектрики (атомы и молекулы таких диэлектриков в отсутствие внешнего электрического поля обладают дипольными моментами, при помещении в электрическое поле дипольные моменты ориентируются преимущественно по направлению вектора напряженности поля).

Н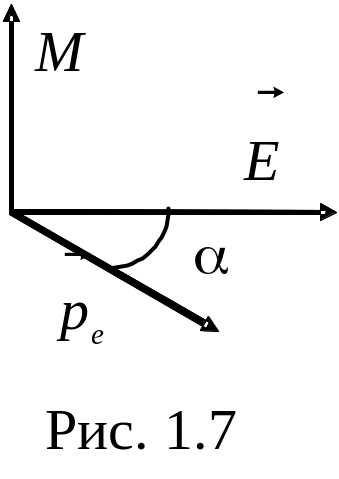 а электрический диполь в электрическом поле действует момент сил, поворачивающий диполь по направлению поля:

, М = р_e·Е·sin.

Электрическое поле совершает работу при ориентации диполя, поэтому электрический диполь во внешнем поле обладает потенциальной энергией

,

где   угол между дипольным моментом и напряженностью поля (рис. 1.7).

Установлению параллельной ориентации всех дипольных моментов препятствует тепловое движение атомов и молекул диэлектрика.

При внесении диэлектрика во внешнее электрическое поле происходит поляризация диэлектрика, состоящая в том, что в любом малом его объёме V возникает отличный от нуля суммарный дипольный электрический момент молекул. Диэлектрик в таком состоянии называется поляризованным. Количественной мерой поляризации диэлектрика служит поляризованность (вектор поляризации) .

Поляризованность равна электрическому дипольному моменту единицы объема диэлектрика:

.

В случае неоднородной поляризации ( ) необходимо рассматривать предел этого отношения, когда V0.

Для однородных и изотропных диэлектриков поляризованность пропорциональна напряженности поля:

,

где   диэлектрическая восприимчивость вещества.

В результате поляризации диэлектрика в тонких слоях у ограничивающих его поверхностей возникают некомпенсированные связанные заряды, называемые поверхностными поляризационными (связанными) зарядами. Поверхностная плотность _связ поляризационных зарядов равна проекции поляризованности на внешнюю нормаль к рассматриваемой поверхности диэлектрика:

,

где   угол между вектором и нормалью к поверхности.

6. Условия для электростатического поля на границе раздела изотропных диэлектрических сред

1. Составляющая вектора напряженности, параллельная границе раздела диэлектриков (тангенциальная составляющая), не изменяется при переходе через границу раздела диэлектриков:

и .

2 Разность нормальных составляющих вектора электрического смещения на границе раздела диэлектриков равна поверхностной плотности свободных электрических зарядов на границе раздела:

_своб. и _своб..

_связ..

Если  _своб = 0, то

и .