Завдання №32

Побудувати формулу для наближеного обчислення коренів

y = ( 1 x 100 ) використовуючи значення

x₀ = 1; y₀ = 1;

x₁ = 25; y₁ = 5;

x₂ = 100; y₂ = 10;

По формулі обчислити .

Відповідь: ( 2.737 )

Розв’язання:

Треба розв’язати завдання 5 для таблиці.

x	1	25	100
y	1	5	10

Завдання №33

Знайти кут між градієнтами функції u = x² + y² – z²

в точках A( ; 0; 0 ) і B( 0; ; 0 )

Відповідь: ( )

Розв’язання:

GRAD u(x,y,z) = { 2x; 2y; -2z };

GRAD u(A) = { 2 ; 0; 0 }; GRAD u(B) = { 0; 2 ; 0 };

Скалярний добуток градієнтів дорівнює нулю, отже кут між ними дорівнює ;

Завдання №34 Дослідити екстремальну точку функції

u = x² + y² + z² – 4x – 8y – 12z + 100

Відповідь: В точці ( 2; 4; 6 ) MIN

Розв’язання:

Екстремальну точку одержимо, розв’язавши СЛАР

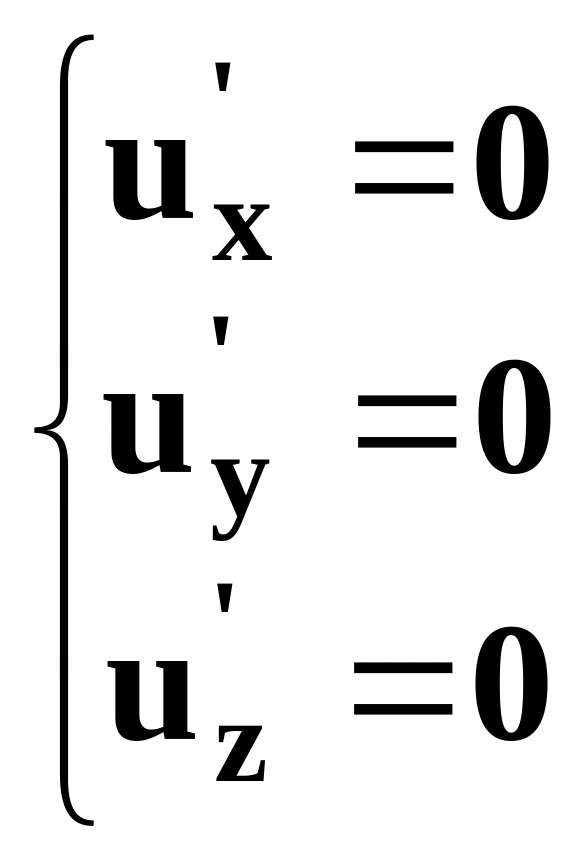
Матриця других похідних додатньо визначена.

=

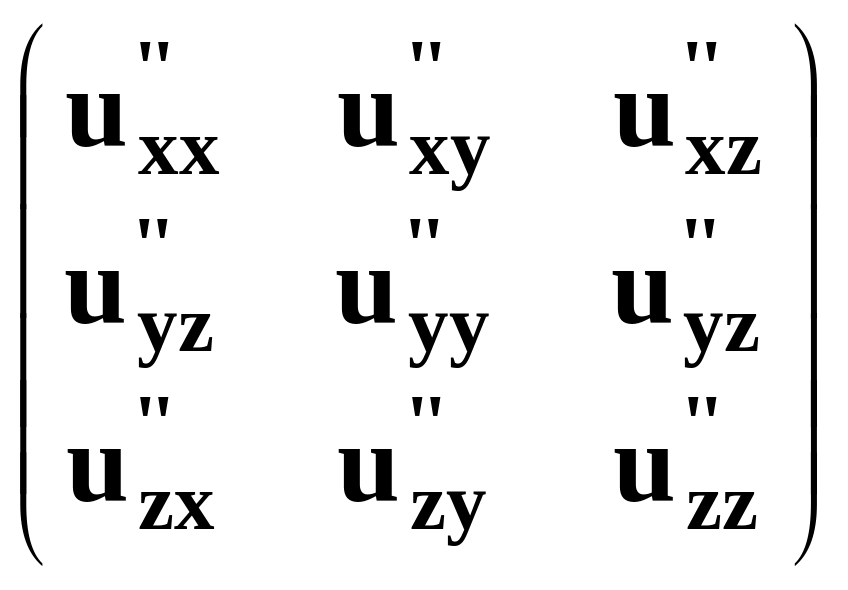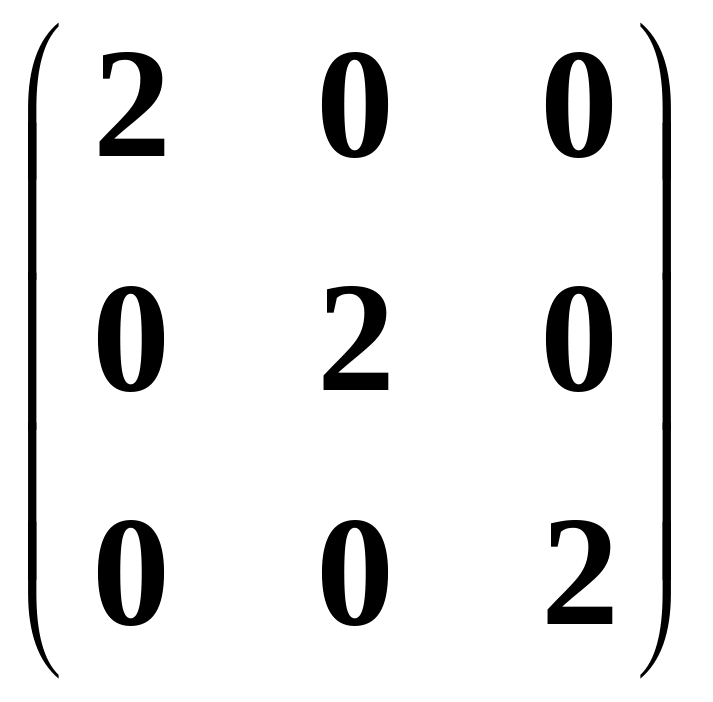
Це означає, що в точці MIN

Завдання №35

Побудувати формулу для наближеного обчислення коренів

y = ( 1 x 27 ) використовуючи значення

x₀ = 1; y₀ = 1;

x₁ = 8; y₁ = 2;

x₂ = 27; y₂ = 3;

По формулі обчислити .

Відповідь: ( 2.2204 )

Розв’язання:

Треба розв’язати завдання 5 для таблиці.

x	1	8	27
y	1	2	3

Завдання №36

Для заданої матриці A побудувати матрицю A^-1

A = ; Відповідь A^-1 = ;

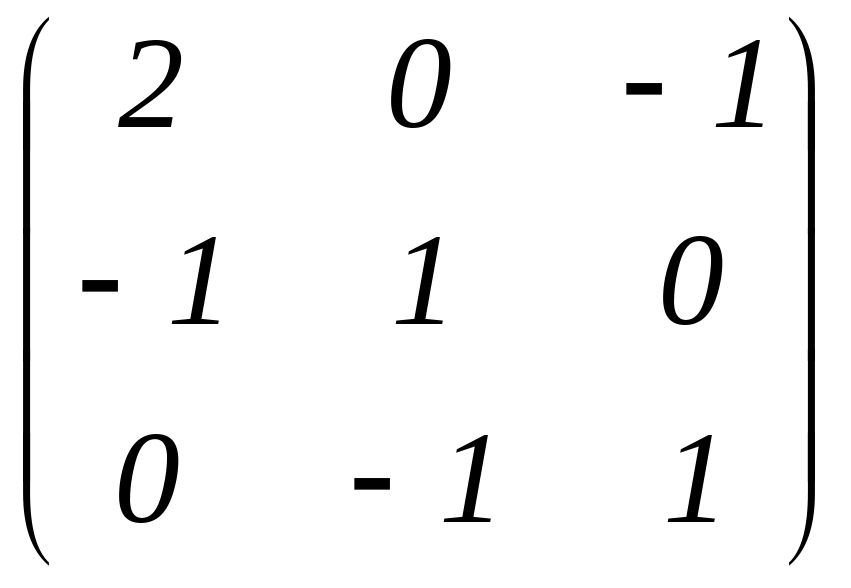Розв’язання:

Стовпчики оберненої матриці послідовно обчислюємо, розв’язуючи СЛАР

= ; = ; =

Завдання №37

Для заданої матриці А обчислити значення її характеристичного полінома

P_n(t) = | A - E | , при = 5 ;

A = ;

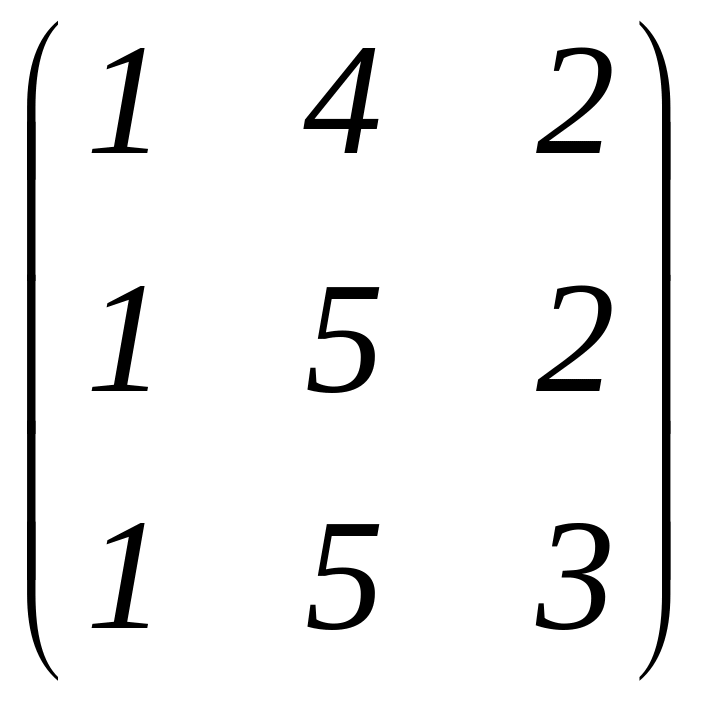Розв’язання:

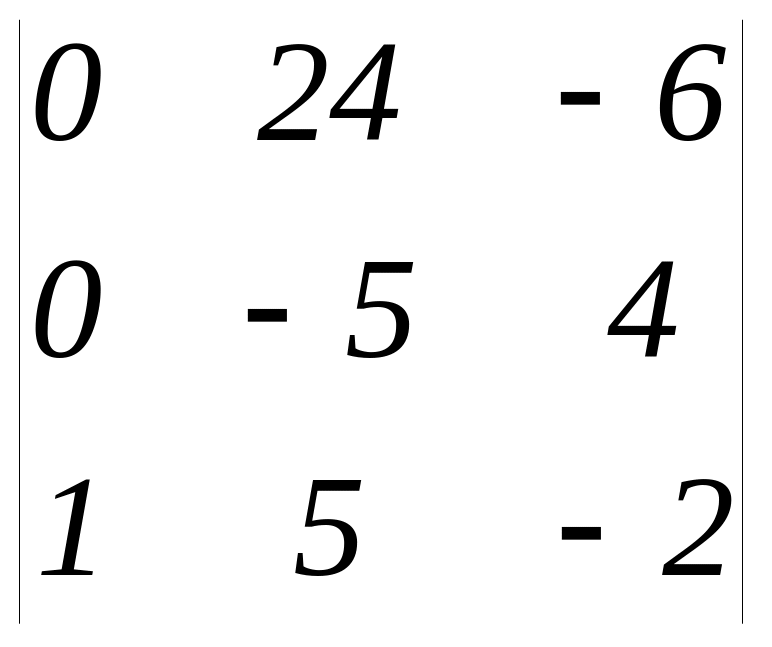= = =96-30=66

Завдання №38

Обчислити визначник методом Гауса.

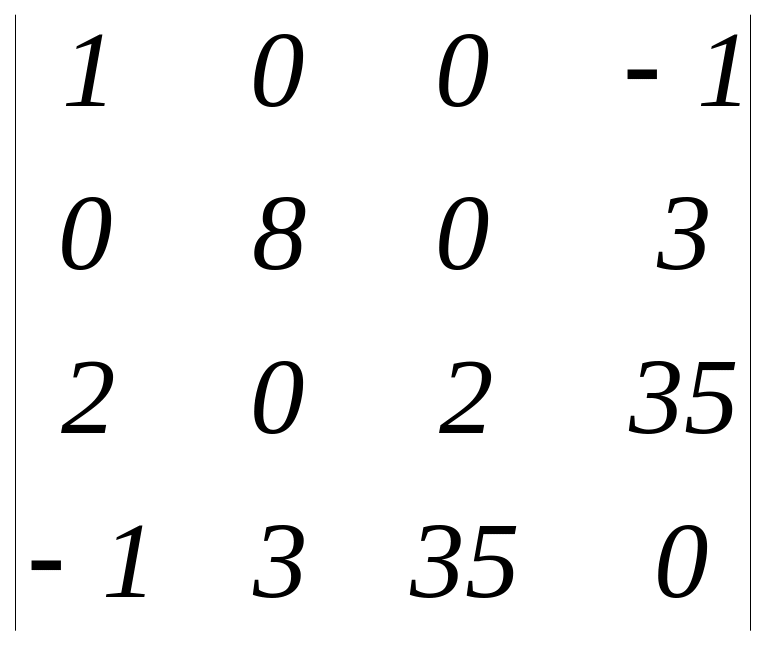
Відповідь: ( -10394 )

Розв’язання:

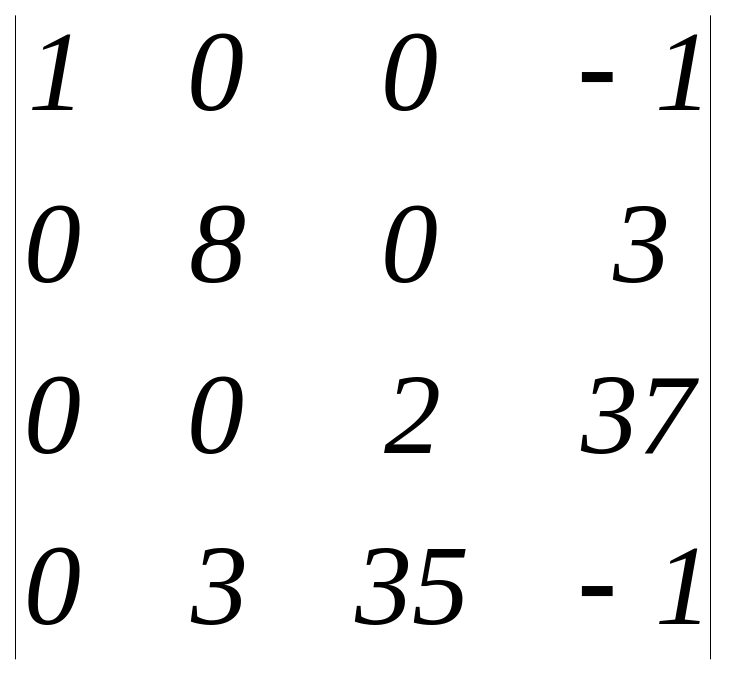
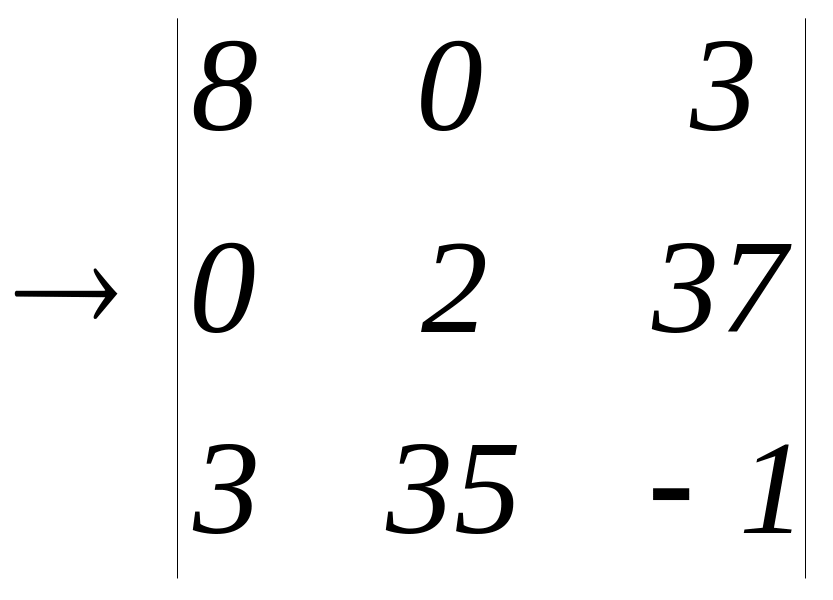8(-2-1295)+3(0-6)=-10394

Завдання №39

Функція f(x) задана таблицею з п’яти точок.

x	-2	-1	0	1	2
y	1	2	2.5	2	1.5

За формулою прямокутників з вузлом у правій точці обчислити

Відповідь: ( 8 )

Розв’язання:

= =2(-1+2) + 2.5(0+1) + 2(1-0) + 1.5(2-1) = 8

Завдання №40

Лінійна густина матеріалу стержня змінюється по закону p = 6 + 0.3x кГ/м ,

де x – відстань від одного з кінців стержня.

Обчислити масу стержня довжиною 10 м.

Відповідь: ( 75 кГ )

Розв’язання:

P= =(6x+0.3 ) = 75;