Завдання №18

Для крайової задачи

з просторовим кроком h=1/3 та часовим кроком =0.1 знайти по неявній різницевій схемі значення розв’язку на першому часовому шарі у точці х=1/3 з точністю до 0.01.

Розв’язання:

Вводимо сітку з вузлами . Для кожного з вузлів замінюємо диференціальне рівняння алгебраїчним по шаблону:

, де .

У даному випадку одержимо систему двох алгебраїчних рівнянь з двома невідомими :

З початкової умови випливає, що .

З крайових умов випливає, що . Тому система має вигляд:

або

Її розв’язок

Завдання №19

Дана система нелінійних алгебраїчних рівнянь

Виконати одну ітерацію методом Ньютона з точністю до 0.01. Початкове наближення: .

Розв’язання:

Метод Ньютона для системи нелінійних алгебраїчних рівнянь вигляду

полягає у розв’язуванні на кожній к-й ітерації системи лінійних алгебраїчних рівнянь наступної структури:

У даному випадку:

і система має структуру

.

Підставимо початкове наближення і одержимо систему

;

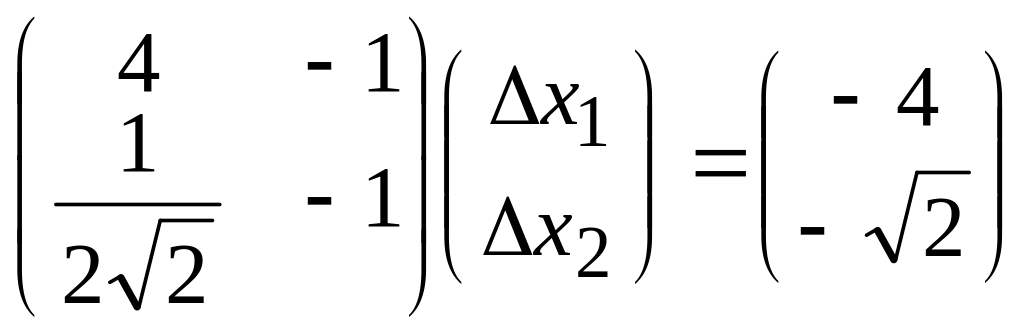Її розв’язок: Δx₁ = -0.71, Δx₂ = 1.16.

Нове наближення:

Завдання №20

Дана система нелінійних алгебраїчних рівнянь

Виконати одну ітерацію методом простої ітерації з точністю до 0.01. Початкове наближення: .

Розв’язання:

Метод простої ітерації для системи нелінійних алгебраїчних рівнянь вигляду

полягає у приведенні її попередньо до вигляду

і виконанні ітерацій

.

У даному випадку:

Підставимо початкове наближення:

Завдання №21

Систему лінійних алгебраїчних рівнянь

розв’язати методом найменших квадратів .

Відповідь: (-0.7, 4.5)

Розв’язання:

Відповідь одержимо, розв’язавши СЛАР виду (A’A)x = (A’b)

= ; = ;

= ;

Завдання №22

Дослідити вид квадратичної форми F(r) = ( r,Ar ), якщо відома її матриця А.

Відповідь: Квадратична форма додатньо визначена

Розв’язання:

Послідовно обчислюємо головні мінори.

M₁=| 6 | = 6; M₂= = 26; M₃= = 294;

Якщо всі головні мінори додатні, то згідно з критерієм Сильвестра квадратична

форма додатньо визначена.

Завдання №23

Швидкість точки змінюється по закону V = 15 + 8*t

Який шлях пройде точка за проміжок часу [ 0; 10 ] .

Відповідь: ( 550 )

Розв’язання:

S= =(15t+8 ) = 550;

Завдання №24

Задані поверхня x² + y² +z² = 169 і точка M₀ ( 3, 4, 12 ) .

Записати рівняння нормалі до поверхні в точці M₀

Розв’язання:

Наша поверхня – сфера з радіусом 169.

Точка М₀ належить сфері.

Нормаль це лінія яка проходить через початок координат ( 0; 0; 0 )

і точку М₀ ( 3; 4; 12 )

Рівняння просторової лінії,

яка проходить через точки ( x₁; y_1; z₁ ) і ( x₂; y_2; z₂ )

; Підставимо числа, одержимо

Завдання №25

Розв’язати задачу лінійного програмування

Z = 40x₁ + 36x₂ Min

при обмеженнях

x₁ 8 ;

x₂ 10 ;

5x₁ + 3x₂ 45 ;

x₁ 0;

x₂ 0 ;

Відповідь: Z_min = 377.6; в точці ( 8; 1.6 )

Розв’язання:

Завдання №26

Знайти похідну функції z = x² – y² в точці M( 1; 1 ) в напрямку, який утворює кут = 60⁰ з додатнім напрямком осі Ox.

Відповідь: 1 -

Розв’язання:

GRAD z(x,y) = { ; } = { 2x; -2y };

={ }; =( n_x + n_y ) = 1 - ;

Завдання №27

Знайти градієнт функції u = x y z в точці M( 1; 2; 3 )

Відповідь: { 6; 3; 2 }

Розв’язання:

GRAD u(x,y,z) = { } = { yz; xz; xy } = { 2*3; 1*3; 1*2 } = { 6; 3; 2 }

Завдання №28

Задано відрізок [ 10; 15 ] . Знайти положення точки Z, яка ділить відрізок у

“ золотому “ відношенні.

Відповідь: ( 11.909830 )

Розв’язання:

Складемо пропорцію = ;

Розкриємо пропорцію 5(Z – 10 ) = ( 15 – Z )² ; Z² - 35Z + 275 = 0;

Менший корінь цього рівняння = 11.909830;

Завдання №29

Обчислити значення квадратичної форми F(r) = ( r,Ar )

в точці r = ( 1; -1; 0 ), якщо матриця А задана

Відповідь: ( -1 )

Розв’язання:

Ar = = ; ( r,Ar ) =[ 1; -1; 0 ] = -1;

Завдання №30

Дослідити на екстремум функцію 2x² + 4xy + y² + 8x при умові x – y = 0 ;

Відповідь: В точці MIN

Розв’язання:

Покладемо x = y; Одержимо :

F = 2x² + 4x ² +x² + 8x; F = 7x² +8x; F = 14x + 8; F = + 14;

Точка єкстремума ; MIN

Завдання №31

Знайти компонент F_n ряду Фібоначчі при n = 17 ;

Відповідь: ( 1597 )

Розв’язання:

Виходячи з початкового відрізку 1, 1, 2, 3, 5, 8. . . .

в якому число 8 є шостим компонентом,

продовжуємо ряд Фібоначчі по правилу, що наступний член дорівнює сумі двох попередніх,

тоді матимемо

1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597

6 10 15 17