Завдання №1

Розв’язати систему рівнянь

методом Гаусса з точністю до 0.1.

Розв’язання:

Обертаємо у нуль елементи, що знаходяться під головною діагоналлю

Одержимо систему з верхньою трикутною матрицею:

Розв’яжемо її підстановкою, починаючи з останнього рівняння:

Завдання №2

Для рівняння виконати одну ітерацію методом Ньютона з початковим значенням (знайти ) та точністю до 0.01 .

Розв’язання:

Метод Ньютона для рівняння реалізується за формулою . У даному випадку:

; ;

;

;

;

;

Завдання №3

Для рівняння виконати одну ітерацію методом хорд (знайти ) з початковим відрізком [0,1] та точністю до 0.1.

Розв’язання:

Метод хорд для рівняння реалізується за формулою . У даному випадку:

; ;

; ;

Завдання №4

Для рівняння виконати одну ітерацію методом половинного ділення (знайти ) з початковим відрізком [0,1] та точністю до 0.1.

Розв’язання:

Метод половинного ділення для рівняння реалізується за формулою . У даному випадку:

;

; ;

;

Завдання №5

Функцiя y=f(x) задана таблицею з трьох точок

x	0	1	3
y	2	0	1

За iнтерполяцiйною формулою Лагранжа обчислити її значення при x=2 та точністю до 0.01.

Розв’язання:

Для трьох вузлів формула Лагранжа має вигляд:

;

Підставимо табличні значення і значення :

Завдання №6

Функцiя y=f(x) задана таблицею з трьох точок

x	0	1	3
y	2	0	1

Побудувати поліном середньоквадратичного наближення першого степеня та обчислити його значення при x=2 з точністю до 0.01.

Розв’язання:

Поліном середньоквадратичного наближення першого степеня будемо шукати у вигляді:

. Для визначення треба побудувати систему нормальних рівнянь такої структури:

У даному випадку:

.

Отже, . Підставимо :

Завдання №7

Функцiя y=f(x) задана таблицею з п’яти точок

x	0	1	2	3	4
y	3	1	0	1	2

Побудувати кусочно-параболічну інтерполюючу функцію та обчислити її значення при x=5 з точністю до 0.1.

Розв’язання:

Для розв’язання задачі згрупуємо табличні точки в часткові відрізки по три точки в кожному. На кожному з часткових відрізків [0,2] , [2,4] за допомогою формули Лагранжа побудуємо інтерполяційний поліном другого степеня.

Для першого відрізка :

На другому відрізку скористаємося цією самою функцією, але як величини тепер будемо використовувати чергові точки таблиці

.

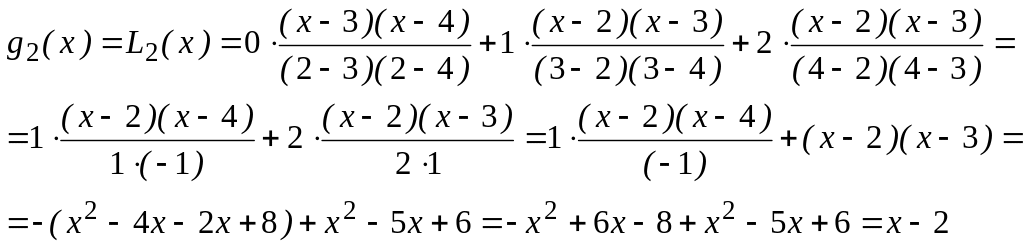
У вираз для другого полінома підставимо :

Завдання №8

Для задачі Коші

виконати один крок явним методом Ейлера (знайти по відомому ) з точністю до 0.1.

Розв′язання

Для рівняння явний метод Ейлера реалізується за формулою . У даному випадку:

y₁ = y₀ + hf( x₀ , y₀ ) = 1 + 0.1(0³+1) = 1.1 .

Завдання №9

Для задачі Коші

виконати один крок неявним методом Ейлера (знайти по відомому ) з точністю до 0.01.

Розв′язання

Для рівняння неявний метод Ейлера реалізується за формулою . У даному випадку:

y₁ = y₀+ hf( x₁ , y₁ ) ;

y₁ = y₀ + 0.1( 0.1³ +y₁ ) ;

y₁ = 1 + 0.1⁴ +0.1y₁ ;

0.9y₁ =1.0001 ;

y₁ = 1.11 .

Завдання №10

Дана крайова задача для ЗДР:

у''-у=2х, у(0)=0, у(1)= -1.

Методом скінчених різниць з кроком h= знайти її розв’язок при х= з точністю до 0.01.

Розв′язання

Вводимо сітку з вузлами . Позначимо . З крайових умов витікає, що .

Для кожного з вузлів замінюємо диференціальне рівняння алгебраїчним:

Одержимо систему двох лінійних алгебраїчних рівнянь відносно , з якої знайдемо шукане .
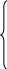