Введение

В наше время новые информационные технологии занимают очень важное место не только в специализированных, но и в повседневных сферах жизни. Компьютеры применяются в бизнесе, менеджменте, торговле, учебе и многих других сферах деятельности человека.

Компьютерные технологии очень удобны для выполнения разнообразных операций, но в разных сферах применения эти операции разные. Потому, каждая отдельная отрасль, которая использует специфические технические средства, нуждается в своих собственных программах, которые обеспечивают работу компьютеров.

Разработкой программного обеспечения занимается такая отрасль науки, как программирование. Она приобретает все большее и большее значение в последнее время, ведь с каждым днем компьютер становится все более необходимым, все более повседневным явлением нашей жизни. Ведь вычислительная техника прошлых лет уже почти полностью исчерпала себя и не удовлетворяет тем потребностям, которые появляются перед человечеством.

Таким образом, новые информационные технологии очень актуальны в наше время и нуждаются в большем внимании для последующей разработки и совершенствования. Рядом с этим, большое значение имеет также и программирование, которое является одним из фундаментальных разделов информатики и потому не может оставаться в стороне.

Программирование содержит целый ряд важных внутренних задач. Одной из наиболее важных задач для программирования является задача сортировки.

Под сортировкой обычно понимают перестановки элементов любой последовательности в определенном порядке.

Эта задача является одной из важнейших потому, что ее целью является облегчение последующей обработки определенных данных и, в первую очередь, задачи поиска. Одним из эффективных алгоритмов поиска является бинарный поиск. Он работает быстрее, чем, например, линейный поиск, но его возможно применять лишь при условии, что последовательность уже упорядочена, то есть отсортирована.

Вообще, известно, что в любой сфере деятельности, которая использует компьютер для записи, обработки и сохранения информации, все данные сохраняются в базах данных, которые также нуждаются в сортировке. Определенная упорядоченность для них очень важна, ведь пользователю намного легче работать с данными, которые имеют определенный порядок.

Задача сортировки в программировании не решена полностью. Ведь, хотя и существует большое количество алгоритмов сортировки, все же целью программирования является не только разработка алгоритмов сортировки элементов, но и разработка именно эффективных алгоритмов сортировки. Мы знаем, что одну и ту же задачу можно решить с помощью разных алгоритмов, и каждый раз изменение алгоритма приводит к новым, более или менее эффективным решениям задачи. Основными требованиями к эффективности алгоритмов сортировки является, прежде всего, эффективность по времени и экономное использование памяти. Согласно этим требованиям, простые алгоритмы сортировки (такие, как сортировка выбором и сортировки включением) не являются очень эффективными.

Алгоритм сортировки обменами, хотя и завершает свою работу (поскольку он использует лишь циклы с параметром и в теле циклов параметры принудительно не изменяются) и не использует вспомогательной памяти, но занимает много времени. Даже, если внутренний цикл не содержит ни одной перестановки, то действия будут повторяться до тех пор, пока не завершится внешний цикл.

Алгоритм сортировки выбором более эффективная сортировка обменами за критерием М(n), то есть за количеством пересылок, но также является не очень эффективным. Из этих причин были разработаны некоторые новые алгоритмы сортировки, которые получили название быстрых алгоритмов сортировки. Это такие алгоритмы, как сортировка деревом, пирамидальная сортировка, быстрая сортировка Хоора и метод цифровой сортировки.

Целью теоретической части курсовой работы является ознакомление с алгоритмами сортировки, попытка проанализировать их и осветить каждый из них.

Как показано выше, реализация очереди с приоритетами с помощью пирамиды имеет то преимущество, что все методы выполняются в логарифмическом времени и даже быстрее. Следовательно, такая реализация удовлетворяет требованиям приложений, где требуется быстрое выполнение всех методов очереди с приоритетами. Поэтому еще раз рассмотрим схему сортировки PriorityQueueSort (п. 7Л.2), в которой для сортировки последовательности S используется очередь Р.

Если реализуется очередь с приоритетами с помощью пирамиды, то в первой стадии каждая из п операций insertltem займет 0(log к) времени, где к — количество элементов пирамиды на этот момент. Аналогично на второй стадии каждая из п операций removeMin будет выполняться за 0(log к) времени, где к — количество элементов пирамиды в текущий момент. Поскольку всегда к < п, каждая такая операция максимально занимает 0(log п) времени. Таким образом, каждая стадия требует 0(п log п) времени, соответственно, при использовании пирамидальной реализации весь алгоритм сортировки очереди с приоритетами будет выполняться за 0(п log п) времени. Такой алгоритм сортировки больше известен как пирамидальная сортировка (heap-sorting), а показатели его производительности приводятся в следующем утверждении.

Утверждение 7.2. Алгоритм пирамидальной сортировки сортирует последовательность S из п сравнимых элементов за O(nlogn) времени.

Из табл. 3.3 видно, что время выполнения 0(п log п) пирамидальной сортировки значительно меньше, чем время выполнения 0(п^[18]) пузырьковой сортировки (раздел 5.4), сортировки методом выбора и сортировки методом ввода (п. 7.2.3).

Реализация внутренней пирамидальной сортировки

Если сортируемая последовательность Sреализована с помощью массива, можно ускорить пирамидальную сортировку и ограничить требования к занимаемой памяти некоторым постоянным фактором, использующим сегмент самой последовательности ?для хранения пирамиды, таким образом избежав применения внешней пирамидальной структуры данных. Этого можно добиться путем модификации алгоритма следующим путем.

часть 5 с индексами от /-1 до п-1 используем для хранения элементов последовательности. Таким образом, первые / элементов (/ = 0, …, /-1) обеспечивают векторное представление пирамиды (с модифицированной нумерацией уровней — от 0 вместо 1), при котором элемент уровня к больше или равен своим дочерним элементам уровня 2к +1 и 2к +2.

2.      На первой стадии алгоритма начнем с пустой пирамиды, и каждый раз на один шаг передвигаем границу между пирамидой и последовательностью слева направо. На шаге / (/ = 1, …, п) увеличиваем пирамиду, добавляя элемент в уровень /-1.

3.      На второй стадии алгоритма начнем с пустой последовательности, и каждый раз на один шаг передвигаем границу между пирамидой и последовательностью справа налево. На шаге / (/’ = 1, …, п) удаляем наибольший элемент из пирамиды и сохраняем его на уровне п – /.

Такая разновидность сортировки пирамиды называется внутренней сортировкой (sort in-place), поскольку в дополнение к самой последовательности используется одно и то же пространство. Вместо передачи элементов из последовательности и обратно производится их реорганизация. Сортировка этого типа представлена на рис. 7.8. В принципе можно говорить о внутренней сортировке, если при этом дополнительно к памяти, необходимой для самих сортируемых объектов, используется некоторый постоянный объем памяти.

Пирамидальная сортировка (англ. Heapsort, «Сортировка кучей»^[1]) — алгоритм сортировки, работающий в худшем, в среднем и в лучшем случае (то есть гарантированно) за Θ(n log n) операций при сортировке n элементов.^[2] Количество применяемой служебной памяти не зависит от размера массива (то есть, O(1)).

Может рассматриваться как усовершенствованная сортировка пузырьком, в которой элемент всплывает (min-heap) / тонет (max-heap) по многим путям.

История создания

Пи­ра­ми­даль­ная сор­ти­ров­ка бы­ла пред­ло­же­на Дж. Уи­льям­сом в 1964 го­ду.

Алгоритм

Сортировка пирамидой использует сортирующее дерево. Сортирующее дерево — это такое двоичное дерево, у которого выполнены условия:

1. Каждый лист имеет глубину л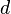ибо  , либо 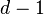 ,   — максимальная глубина дерева.

2. Значение в любой вершине не меньше (другой вариант — не больше) значения её потомков.

Удобная структура данных для сортирующего дерева — такой массив Array, что Array[1] — элемент в корне, а потомки элементаArray[i] являются Array[2i] и Array[2i+1].

Алгоритм сортировки будет состоять из двух основных шагов:

1. Выстраиваем элементы массива в виде сортирующего дерева:

при  .

Этот шаг требует   операций.

2. Будем удалять элементы из корня по одному за раз и перестраивать дерево. То есть на первом шаге обмениваем Array[1] и Array[n], преобразовываем Array[1], Array[2], … , Array[n-1] в сортирующее дерево. Затем переставляем Array[1] и Array[n-1], преобразовываем Array[1], Array[2], … ,Array[n-2] в сортирующее дерево. Процесс продолжается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда Array[1], Array[2], … , Array[n] — упорядоченная последовательность.

Этот шаг требует   операций.

Достоинства и недостатки

Достоинства

• Имеет доказанную оценку худшего случая  .

• Сортирует на месте, то есть требует всего O(1) дополнительной памяти (если дерево организовывать так, как показано выше).

Недостатки

• Сложен в реализации.

• Неустойчив — для обеспечения устойчивости нужно расширять ключ.

• На почти отсортированных массивах работает столь же долго, как и на хаотических данных.

• На одном шаге выборку приходится делать хаотично по всей длине массива — поэтому алгоритм плохо сочетается с кэшированием и подкачкой памяти.

• Не работает на связанных списках и других структурах памяти последовательного доступа.

Пирамидальная сортировка. Будем называть файл ключей K1, K2, ..., KN "пирамидой", если

K  j/2

≥ Kj

при 1≤   j/2 < j ≤ N (1)

В этом случае K1

≥ K2,K1

≥ K3, K2

≥ K4

и т. д. Именно это условие выполняется на рис. 1. Из

него следует, в частности, что наибольший ключ оказывается "на вершине пирамиды":

max( , ,..., ) K1

= K1

K2

K

N

(2)

Если бы мы сумели как-нибудь преобразовать произвольный исходный файл в пирамиду, то

для получения эффективного алгоритма сортировки можно было бы воспользоваться

"нисходящей" процедурой выбора, подобной той, которая описана выше.

Эффективный подход к задаче построения пирамиды предложил Р. У. Флойд [САСМ, 7

(1964), 701]. Пусть нам удалось расположить файл таким oбразом, что

K  j/2

≥ Kj

при l ≤   j /2 < j ≤ N (3)

где lóнекоторое число ≥1. (В исходном файле это условие выполняется "автоматически" для

l =   N/2 , поскольку ни один индекс j не удовлетворяет условию    N/2 < j/2 < j ≤ N.)

Нетрудно понять, как, изменяя лишь поддерево с корнем в узле l, преобразовать файл, чтобыраспространить неравенства (3) и на случай, когда   j/2 = l . Следовательно, можно

уменьшать l на единицу, пока в конце концов не будет достигнуто условие (1). Эти идеи

Уильямса и Флойда приводят к изящному алгоритму, который заслуживает пристального

изучения.

Алгоритм Н. (Пирамидальная сортировка.) Записи R1, ..., R

N переразмещаются на том же

месте; после завершения сортировки их ключи будут упорядочены: K1

≤ ... ≤ KN. Сначала

файл перестраивается в пирамиду, после чего вершина пирамиды многократно исключается

и записывается на свое окончательное место. Предполагается, чтоN ≥ 2.

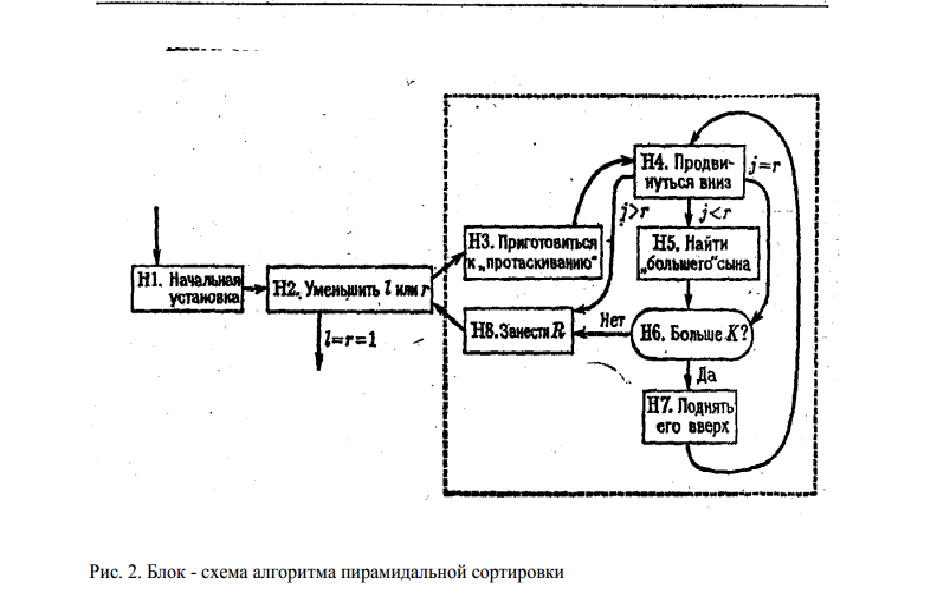
H1. [Начальная установка.] Установить l ←   N/2 +1, r!N.

Н2. [Уменьшить l или r.] Если l > 1, то установить l ! l-1, R ! Rl

, K ! Kl

(Если l >1,

это означает, что происходит процесс преобразования исходного файла в пирамиду;

если же l = 1, то это значит, что ключи K1, K2, ..., Kr

уже образуют пирамиду.)

В противном случае установить R ! Rr, K ! Kr, Rr

! R1, r! r - 1; если в результате

оказалось, что r = 1, то установить R1

! R и завершить работу алгоритма.

Н3. [Приготовиться к "протаскиванию".] Установить j ! l. (К этомумоменту

K  j/2

≥ Kj

при l <   j/2 < j ≤ r, (4)

а записи Rk, r < k ≤ N, занимают свои окончательные места. Шаги Н3 ó Н8

называются алгоритмом "протаскивания"; их действие эквивалентно установке Rl ! R

с последующим перемещением записей Rl

, ..., Rr

таким образом, чтобы условие (4)

выполнялось и при   j/2 = l .)

Н4. [Продвинуться вниз.] Установить i ! j и j ← 2j. (В последующих шагах i =   j/2 .)

Если j < r, то перейти к шагу Н5; .если j = r, то перейти к шагу Н6; если же j > r,

то перейти к шагуН8.

Н5. [Найти "большего" сына.] Если Kj < Kj+1, то установить j ← j+1.

Н6. [БольшеK?] Если К≥ Кj

, то перейти к шагуН8.

Н7. [Поднять его вверх.] Установить Ri

← Rj

и возвратиться к шагуН4.

Н8. [Занести R.] Установить Ri

← R. (На этом алгоритм "протаскивания", начатый

в шаге НЗ, заканчивается.) Возвратиться к шагу Н2.

Пирамидальную сортировку иногда описывают как - алгоритм, это обозначение указывает

на характер изменения переменных l и r. Верхний треугольник соответствует фазе

построения пирамиды, когда r = N, а l убывает до 1; нижний треугольник представляет фазу

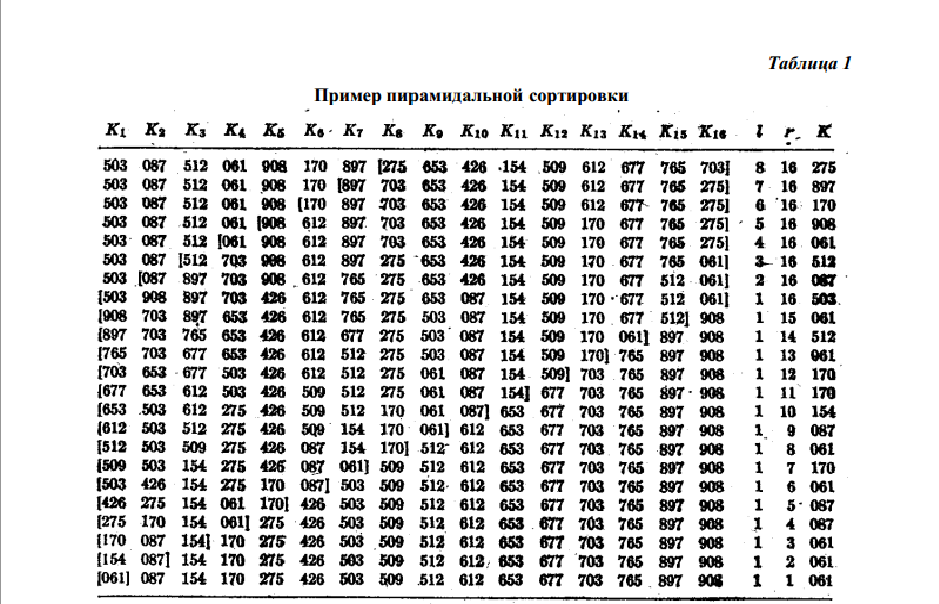
выбора, когда l = 1, а r убывает до 1. В табл. 1 показан процесс пирамидальной сортировки

все тех же шестнадцати чисел. (В каждой строке изображено состояние после шага Н2,

скобки указывают на значения переменных l и r.). Блок-схема алгоритма пирамидальной

сортировки приведена на рис. 2.

Программа, основанная на рассмотреном алгоритме, будет приблизительно лишь вдвое

длиннее программы, построенной по алгоритму S, но при больших N она гораздо более

эффективна. Ее время работызависит от:

P= N+   N/2 − 2= число "протаскиваний";

А = число протаскиваний, при которых ключКв конце попадает во внутренний узел

пирамиды;

В =суммарное число ключей, просмотренных во время протаскиваний;

С = число присваиваний j ← j + 1 в шаге Н5;

D = число случаев, когда в шаге Н4 j = r.

Эти величины проанализированы ниже. Как показывает практика, они сравнительно мало

отклоняются от своих средних значений:

A≈ 0.349N; B≈ Nlog2

N−1.87N; C Nlog N 0.9N

2

1

≈ 2

− ; D ≈ lnN. (5)

При N = 1000, например, четыре эксперимента со случайными исходными данными

показали соответственно результаты (А, В, С, D) = (371, 8055, 4056, 12),

(351, 8072, 4087, 14), (341, 8094, 4017, 8), (340, 8108, 4083, 13).

Общее время работы 7A+14B+4C+20N-2D+15  N/2 -28 равно, таким образом, в среднем

примерно 16Nlog2

N+ 0.2N единиц.

Глядя на табл. 1, трудно поверить в то, что пирамидальная сортировка так уж эффективна:

большие ключи перемещаются влево прежде, чем мы успеваем отложить их вправо! Это и в

самом деле странный способ сортировки при малых N. Время сортировки 16 ключей из табл.

1 равно 1068 ед., тогда как обычный метод простых вставок требует всего 514 ед. При

сортировке простым выбором требуется 853 ед.

При больших N алгоритм Н более эффективен. Напрашивается сравнение с сортировкой

методом Шелла с убывающим шагом и быстрой сортировкой Хоара, так как во всех трех

алгоритмах сортировка производится путем сравнения ключей, причем вспомогательной

памяти используется мало или она не используется вовсе. При N=1000 средние времена

работыравныприблизительно

160000 ед. для пирамидальной сортировки;

130000 ед. для сортировки методомШелла;

80000 ед. для быстрой сортировки.

С ростом N пирамидальная сортировка превзойдет по скорости метод Шелла, но

асимптотическая формула 16Nlog2

N ≈ 23.08NlnN никогда не станет лучше выражения для

быстрой сортировки 12.67NlnN. С другой стороны, быстрая сортировка эффективна лишь в

среднем; в наихудшем случае ее время работы пропорционально N

2

. Пирамидальная же

сортировка обладает тем интересным свойством, что для нее наихудший случай не намного

хуже среднего. Всегда выполняются неравенства

A≤1.5N, B≤ N  log2

N , C ≤ N  log2

N ; (6)

таким образом, независимо от распределения исходных данных выполнение алгоритма Н не

займет более 18N  log2

N + 38N единиц времени. Пирамидальная сортировка ó первый из

рассмотренных нами до сих пор методов сортировки, время работы которого заведомо имеет

порядок N log N. Сортировка посредством слияний, которую мы обсудим позднее, тоже

обладает этим свойством, но она требует больше памяти.

Пирамидальная сортировка в некотором роде является модификацией что минимальный(или максимальный) элемент из неотсортированной последовательности выбирается не за O(n) операций, а за O(log n). Соответственно и производительность такого метода будет не ~ O(n²), такого подхода, как сортировка выбором, с тем лишь отличием, а O(n*log n), т.е. наиболее быстрая для сортировки. Естественно, без дополнительных манипуляций с неотсортированной последовательностью мы не добьемся выбора из нее максимального(в пирамидальной сортировке выбирается максимальный, поэтому дальше будем это всегда предполагать) элемента за O(log n). Точнее, для такого быстрого выбора из этой неотсортированной последовательности строится некоторая структура. И вот именно суть метода пирамидальной сортировки и состоит в построении такой структуры, называемой соответственно "пирамидой".