1.2.3. Комплексные показатели надежности

К основным комплексным показателям надежности относятся: коэффициент готовности и коэффициент простоя.

Коэффициент готовности - это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.

Этот показатель одновременно оценивает свойства работоспособности и ремонтопригодности объекта.

Для ремонтируемого объекта коэффициент готовности определяется как:

К_г = или К_г = , (1.23)

где t_i - интервалы работоспособного состояния объекта;

τ_i - интервалы неработоспособного состояния объекта;

- среднее время наработки на отказ;

- среднее время восстановления.

Коэффициент простоя также является комплексным показателем надежности.

Коэффициент простоя - это вероятность того, что рассматриваемый объект будет в нерабочем состоянии.

К_п(t) = 1 – К_г(t) = = (1.24)

Коэффициент простоя может быть вычислен непосредственно через основные показатели надежности:

, если Т_В < 1, а значение Т в исходных данных приводится в годах, то можно упростить формулу до вида:

K_П= T_{B · ω = q .} (1.25)

Этот коэффициент является также вероятностью нахождения в неработоспособном состоянии (q).

Если значение Т_В приводится в часах, то

K_П= q = T_{B · ω /8760} (1.26)

Таким образом, вероятность состояния отказа элемента за достаточно большой промежуток времени (не менее года) равна произведению среднего времени восстановления и параметра потока отказов (интенсивность отказов), то есть практически по удельной повреждаемости оборудования и среднему времени восстановления можно определить средние вероятности состояния отказа и рабочего состояния.

По аналогии с коэффициентом простоя можно определить коэффициент планового ремонтного простоя, или коэффициент ремонтного режима:

K_П.Р.= T_{B П.Р. · ωП.Р. /8760 .} (1.27)

Этот коэффициент является также вероятностью нахождения в плановом простое q_П.Р..

Часто используемый в расчетах надежности комплексный показатель – опасность отказа (ρ) и опасность нахождения в планово-предупредительном ремонте (ρ_ППР). Этот показатель равен отношению времени восстановления (продолжительности ППР) и времени безотказной работы (времени между окончанием предыдущего и началом следующего ППР) :

ρ = ; ρ = (1.28)

1.2.4. Последовательное соединение элементов систем электроснабжения

Последовательное соединение элементов является частым соединением элементов в электроснабжении. В понятии отказа заложен физический аналог электрической схемы с последовательным включением элементов (рис.1.3).

Рис. 1.3. Последовательное соединение элементов

Предположим, что система состоит из n последовательно включенных элементов (рис. 1.3). Из теории вероятностей известно, что если определены вероятности появления нескольких независимых случайных событий, то совпадение этих событий определяется как произведение вероятностей их появлений. Система будет находиться в работоспособном состоянии только при условии совпадения работоспособных состояний всех элементов. Таким образом, работоспособность системы оценивается как произведение вероятностей безотказной работы элементов:

, (1.29)

где - вероятность безотказной работы i-го элемента.

Полагая , имеем

Р_С = , (1.30)

где ω _Σ= ω₁ + ω₂ + …+ ω_n =

Соответственно, значение среднего времени безотказной работы

(1.31)

и будет определяться как среднее время наработки на отказ.

Если представить как интенсивность отказов системы, сведенной к эквивалентному элементу с интенсивностью отказов 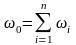= const, то систему из n последовательно включенных элементов легко заменить эквивалентным элементом, который имеет экспоненциальный закон распределения вероятности безотказной работы. А это значит, если ω_o = const, то средняя наработка на отказ системы . Верно также и то, что при условии ω_o= const, искомая величина определится как .

Средняя наработка на отказ системы определяется по выражению:

(1.32)

Если ω(t) зависит от времени, то при произвольном законе распределения времени, наработка на отказ для каждого из элементов равна:

, (1.33)

где ω_i(t) - интенсивность отказов i-го элемента.

Вероятность безотказной работы системы соответственно определяется как

(1.34)

По выражению (1.34) можно определить вероятность безотказной работы системы до первого отказа при любом законе изменения интенсивности отказов каждого из n элементов во времени.