1.2.2 Единичные и комплексные показатели для восстанавливаемых объектов

Процесс функционирования восстанавливаемого объекта можно представить как последовательность чередующихся интервалов работоспособности и восстановления (простоя) (рис.1.2).

Рис. 1.2 – График функционирования восстанавливаемого объекта.

(t₁ …t_n – интервалы работоспособности,τ₁ …τ_n – интервалы восстановления)

Количественным покателем свойства безотказности в цикле работ может служить вероятность безотказной работы. . На практике принимают Р(t) постоянной для всех циклов, хотя после ремонтов вероятности безотказной работы Р(t) для различных циклов различны.

Системы эл сн относятся к вост-м системам. Для таких систем показателем безо-ти является парам пот отказов, ω, 1/год. и вероятность безотказной работы (или вероятность отказа).

Параметр потока отказов представляет собой плотность вероятности возникновения отказа восстанавливаемого объекта.

Другими словами поток отказов, это математическое ожидание числа отказов в единицу времени.

, (1.13)

где вероятность того, что в течении промежутка времени произойдет не мнее одного отказа.

По статистическим данным среднее значение потока отказов определяется с помощью формулы:

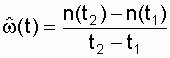, (1.14)

где n(t₁) и n(t₂) - количество отказов объекта, зафиксированных, соответственно, по истечении времени t₁ и t_2.

Если используются данные об отказах по определенному количеству восстанавливаемых объектов, то

, (1.15)

где n(Δt_i) - количество отказов за интервал времени Δt_i;

N - количество однотипных объектов, участвующих в эксперименте (отказавший объект восстанавливается, поэтому N = соnst).

Эта характеристика аналогична средней интенсивности отказов для невосстанавливаемых объектов ( = λ).

Для восстанавливаемых ЭУ в период их нормальной работы вероятность безотказной работы определяется формулой

(1.16)

Средняя наработка на отказ восстанавливаемых объектов – это показатель, характеризующий объекты, при эксплуатации которых допускаются многократно повторяющиеся отказы. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работу и продолжает работу до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до следующего отказа и т.д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений - поток восстановлений. Средняя наработка на отказ для восстанавливаемых объектов равна

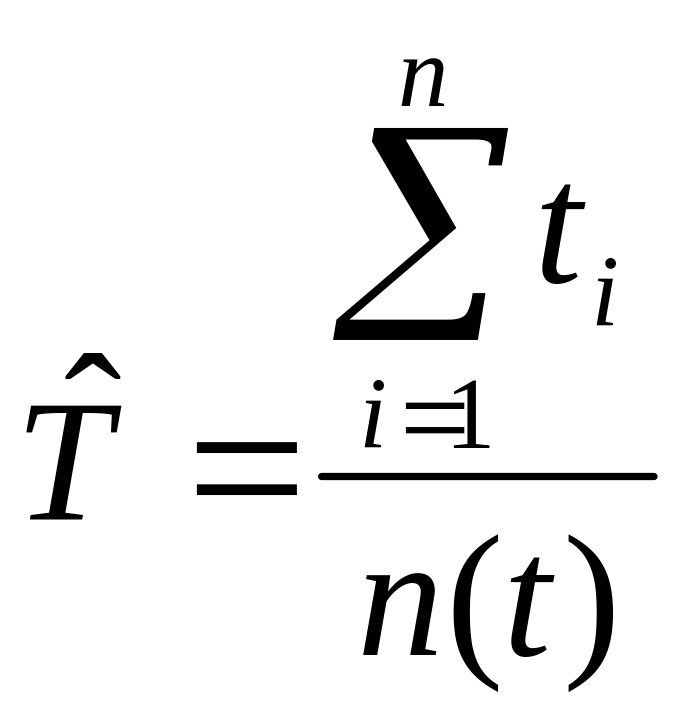, (1.17)

где t_i - наработка между i-1 и i-м отказами, ч;

n(t) - суммарное число отказов за время t.

Другими словами, средняя наработка на отказ - это математическое ожидание времени между двумя ближайшими последовательными отказами.

Для периода работы при экспоненциальном законе распределения справедливы следующее формулы

или ω = λ = (1.18)

Ремонтопригодность восстанавливаемых объектов характеризуется веротностью восстановления в заданое время T, средним временним восстановления Т_в и интенсивностью ремонта.

Функция вероятости восстановления есть количесвенная мера ремонтопригодности означающея, что обьект будет отремонтирован за время t c вероятностью , где Т некое заданое время.

Вероятость восстанавления (применяя экспоненциальный закон распределения вероятности) можно вычислить по формуле:

(1.19)

где μ – интенсивность восстановления.

Интенсивность восстановления - это отношение условной плотности вероятности восстановления работоспособного состояния объекта в некоторый момент t при условии, что до этого момента восстановление не было завершено.

Аналитическая формула интенсивности восстановления имеет вид

, (1.20)

где .

Статистическая оценка этого показателя определяется как:

, (1.21)

где n_в(Δt) - количество восстановлений однотипных объектов за интервал Δt;

N_н.ср - среднее количество объектов, находящихся в не восстановленном состоянии на интервале Δt.

У большинства электроэнергетических объектов поток восстановлений близок к экспоненциальному. Используя свойства этого распределения, запишем зависимость, связывающую среднее время восстановления и интенсивность восстановления:

или (1.22)