3.2 Расчёт геометрических параметров зубчатой передачи

Межосевое расстояние цилиндрической зубчатой передачи из условия контактной выносливости активных поверхностей зубьев

, (3.10)

где – коэффициент, равный 43 для косозубых колёс;

u – передаточное число зубчатой пары;

Т₂ – момент на колесе (большем из колёс);

– коэффициент, учитывающий неравномерность распределения

нагрузки по ширине венца;

– допускаемое контактное напряжение;

– коэффициент ширины венца по межосевому расстоянию.

Передаточное число u=i_з=4, а Т₃=101,04Н·м; =422,6 МПа;

(2.с.32)

коэффициент ширины венца по межосевому расстоянию для косозубых колес (2. с.33)

Межосевое расстояние округляем до стандартного значения 100 мм (2. с.36)

Нормальный модуль (2.с.36) m_н = (0,01…0,02)  = (0,01…0,02) 100 = =1…2 мм. Принимаем m = 2 мм. (2.с.36)

Предварительно принимаем угол наклона зубьев  = 15 (2.с.37).

Тогда число зубьев шестерни:

Принимаем Z₂ = 19

Тогда число зубьев колеса Z_з = Z₂u = 194 = 76

Уточненное значение:

Проверим условие (2. с.36).

Условие выполняется так как 0,4>0,16

Делительный диаметр шестерни и колеса:

мм, 160 мм.

Проверка:

.

Диаметры вершин зубьев шестерни и колеса:

Диаметры впадин зубьев

Ширина колеса:

b_з = _ba = 0,4100 = 40 мм

Ширина шестерни:

b₂ = b_з+5 = 40+5 = 45 мм

Коэффициент ширины шестерни по диаметру:

_bd2 = b₂/d₂ = 45 /40 = 1,125

3.3. Проверочный расчёт зубьев передачи

3.3.1. Расчётное контактное напряжение

, (3.11)

где K_H – коэффициент нагрузки;

b – ширина колеса расчётная (наименьшая).

Окружная скорость колёс

м/с

При такой скорости назначаем восьмую степень точности (2.с.32).

Коэффициент нагрузки при проверочном расчёте на контактную прочность

(3.12)

где – коэффициент, учитывающий неравномерность распределения на-

грузки между зубьями;

– коэффициент, учитывающий неравномерность распределения на-

грузки по длине зуба;

– коэффициент, учитывающий дополнительные динамические на-

грузки.

По рекомендациям (2. с.39-40) назначим следующие значения коэффициентов:

– = 1.09 при окружной скорости =2,0 м/с и восьмой степени точности;

– = 1,04 при значении коэффициента =1,125 и твёрдости зубьев менее НВ 350;

– = 1 при <5 м/с, восьмой степени точности и менее НВ 350.

Расчет по формуле (3.12) дает .

МПа

Условие прочности выполняется.

3.3.1 Расчет зубьев на контактную прочность по формуле (3.11) при кратковременных перегрузках моментом 227,34 Нм дает

3.3.3 Напряжение изгиба зубьев косозубых цилиндрических колёс при проверочном расчёте на выносливость.

Напряжение изгиба зубьев косозубых цилиндрических колёс при проверочном расчёте на выносливость вычисляется по формуле (2. с.46)

(3.13)

где F_t – окружная сила;

K_F – коэффициент нагрузки;

Y_F – коэффициент формы зуба;

Y_β – коэффициент, компенсирующий погрешности, возникающие из-за

применения для косых зубьев той же расчётной схемы, что и для

прямых;

K_FA – коэффициент, учитывающий неравномерность распределения на

грузки между зубьями;

b – ширина колеса, находящаяся в зацеплении, мм;

– модуль нормальный, мм;

В зацеплении колёс быстроходной передачи действуют следующие силы:

– окружная H;

– радиальная Н;

– осевая Н.

Коэффициент нагрузки (2. с.42)

где – коэффициент, учитывающий неравномерность распределения на-

грузки по длине зубьев;

– коэффициент, учитывающий дополнительные динамические на

грузки.

Примем (4,с.43) =1,1; =1,1, тогда

=1,1·1,1=1,21

Без расчётов, руководствуясь только рекомендацией (2.с.47), возьмём К_Fα=0.92.

Коэффициент Y_β определим по формуле (2. с.46):

Коэффициент формы зуба зависит от эквивалентного числа зубьев:

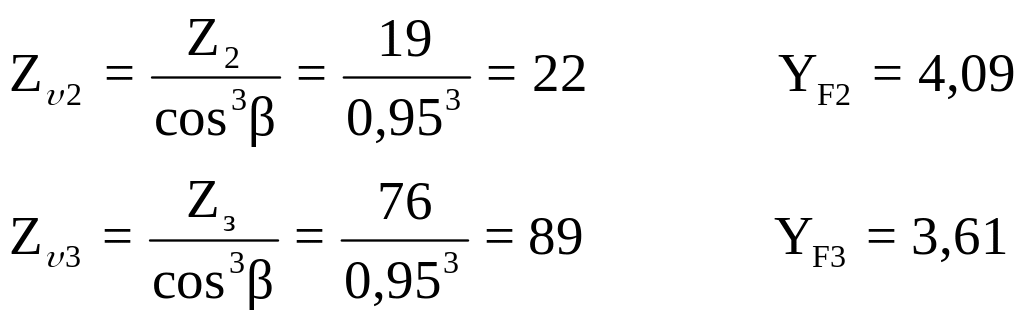
Расчет по формуле (3.13) дает (в МПа):

Это значительно меньше вычисленных в пункте 3.1.4 допускаемых напряжений.

3.3.4 Напряжение изгиба при кратковременных перегрузках

Напряжение изгиба при кратковременных перегрузках вычисляются также по формуле (3.13) куда вместо окружной силы F_t следует подставить окружную силу при кратковрем6263енных перегрузках

После подстановки получаем при перегрузках соответственно для шестерни и колеса напряжение изгиба

МПа

МПа

Эти напряжения значительно меньше вычисленных в пункте 3.1.5

3.3.5 Геометрические параметры колес зубчатой передачи, обоснованные в результате расчетов, сведены в таблицу 3.1.

Таблица 3.1 – Геометрические параметры колес зубчатой передачи

Параметры	Шестерня	Колесо
Межосевое расстояние, мм	100	100
Нормальный модуль, мм	2,0	2,0
Угол наклона зубьев, град
Число зубьев	19	76
Направление зубьев	левое и правое	правое и левое
Делительные диаметры, мм	40	160
Диаметры вершин зубьев, мм	44	164
Ширина венцов колёс,мм	45	40

4. Расчет цепной передачи

4.1 Подбирать будем двухрядную роликовую цепь.

Для расчета приняты следующие исходные данные:

- вращающий момент на ведущей звездочке

- частота вращения ведущей звездочки

- передаточное число передачи

- передача расположена с наклоном линии центров звездочек менее

- смазка цепи периодическая

- натяжение цепи регулируется периодически перемещением одной из звездочек

-кратковременные перегрузки достигают 200% от номинальной нагрузки

- работа привода двухсменная

4.2 Число зубьев ведущей звездочки /2, с.148/

Число зубьев ведомой звездочки

Тогда передаточное отношение равно

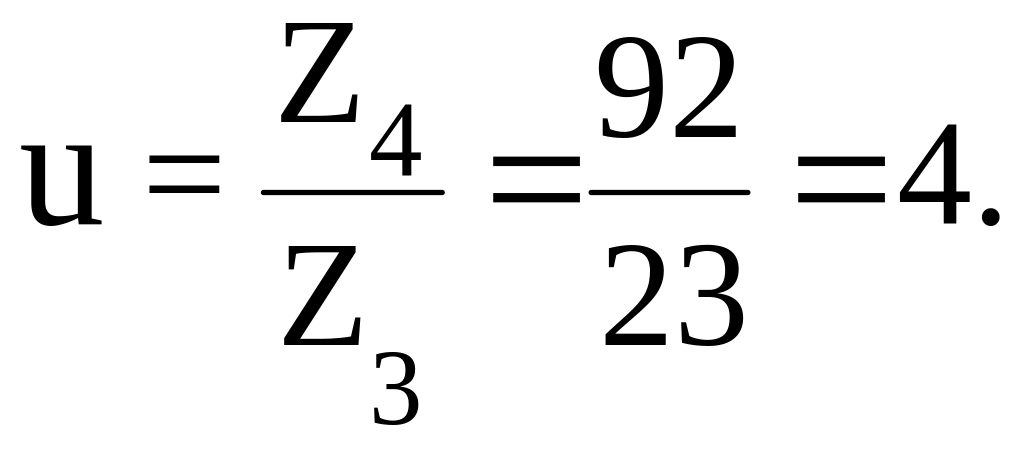
Относительное расхождение с принятым ранее составляет

что меньше допускаемого расхождения 3%.

7.3 Шаг роликовой цепи в миллиметрах ориентировочно вычисляется

(4.1)

где – вращающий момент на ведущей звездочке, Н*м;

– расчётный коэффициент нагрузке;

– число зубьев ведущей звездочки;

[ р ] – допускаемое давление в шарнире цепи, МПа;

m- число рядов цепи.

Ранее уже определено , m=2.

Расчетный коэффициент нагрузки /2, с.149/

(4.2 )

где - динамический коэффициент;

- коэффициент, учитывающий влияние межосевого расстояния;

- коэффициент, учитывающий угол наклона линии центров передачи;

- коэффициент, учитывающий способ регулирования передачи;

- коэффициент, учитывающий способ смазывания передачи;

- коэффициент, учитывающий периодичность работы передачи (коэффициент сменности).

При периодическом регулировании натяжения цепи передачи /2, с.150/. При периодическом смазывании передачи /2, с.150/. При работе в одну смену /2, с.150/.

Расчётный коэффициент нагрузки при расчёте по формуле (4.2) равен

Поскольку шаг цепи неизвестен, то ориентируясь лишь частотой вращения ведущей звездочки принимаем предварительное значение среднего допускаемого давления в шарнире [ р ]= 17 МПа /2, с.150/. Число рядов цепи m=2

Расчетный шаг цепи

4.4 Ближайшие по шагу стандартные двухрядные роликовые цепи имеют нижеследующие характеристики /2, с.147/:

Обозначение цепи по ГОСТ 13568-75	2ПР-19,05-72000	2ПР-25,4-11340
Шаг t ,мм	19,05	25,4
Разрушающая нагрузка Q не менее, кН	72	113,4
Масса одного метра цепи q, кг/м	3,5	5,0
Площадь шарнира Аоп, мм2	211	359
Габаритная ширина цепи b,мм	54	68
Расстояние между рядами А, мм	25,50	29,29
Расстояние изнутри между пластинами одного ряда ,мм	12,70	15,88

4.5 Проверим первоначально цепь 2ПР-19,05-72000

Скорость цепи /2,с.153

Окружная сила

Давление в шарнире цепи /2,с.150 / при площади сечения шарнира Аоп=211 мм²

Уточненное допускаемое давление в шарнире цепи при шаге t= 19,05 мм, числе зубьев малой звездочки и ее частоте вращения /2,с.150

[р]= 23,5 × (1 + 0,01 × (Z₃ – 17)) = 23,5 × (1 + 0,01 × (23 – 17)) = 24,91 МПа

Условие р < [ р ] выполнено.Поэтому окончательно выбираем двухрядную роликовую цепь 2ПР-19,05-72000 по ГОСТ13568-75

4.7 Число звеньев цепи /2,с 148/

(4.3)

Где

Расчёт величин, входящих в формулу (4.3) получим

Число звеньев цепи при расчёте по формуле (4.3) равно

Округляем до ближайшего целого числа

4.7 Уточненное значение межосевого расстояния /2.с 149/

Для свободного провисания цепи в конструкции передачи должна быть предусмотрена возможность уменьшения межосевого расстояния на 0,4%, т.е. на Округлим это значение до 10мм

Для восстановления натяжения цепи по мере её износа конструкция передачи должна предусматривать также увеличение межосевого расстояния на 3%, т.е. на Округлим эту цифру до 30мм

4.8 Диаметры делительных окружностей звездочек /2, с.148/:

Диаметр внешних окружностей звездочек при диаметре ролика цепи /2, с.147/

мм

4.9 Силы, действующие на цепь /2, с.151/:

- окружная

- центробежная

- от провисания цепи. При максимально возможном коэффициенте

К_F = 6/ горизонтальное расположение линии центров звездочек/сила имеет величину

= =159,98 Н

4.10 Расчетная нагрузка,действующая на валы цепной передачи

4.11 Коэффициент запаса прочности цепи при разрушающей нагрузке Q=60,0 кН /2, с.151/

что больше нормативного коэффициента запаса прочности [ S ] = 8,4 /2, с.151/

Литература:

1. Жингаровский А. Н., Кейн Е. И., Коновалов М. Н. Задания к расчетным работам по теории механизмов и машин: Методические указания. – Ухта: УГТУ, 2008. – 37с, ил.

2. Курсовое проектирование деталей машин: учебное пособие для учащихся Машиностроительных специальностей техникумов / С.А. Чернавский, К.Н. Боков, И.М. Чернин и др. 2-е изд., перераб. и доп. – М.: Машиностроение, 1988. – 416 с.

3. Гузенков П.Г. Детали машин: Учеб. пособие для студентов втузов / П.Г. Гузенков– 3-е изд., перераб. и доп. – М.: Высш. школа, 1982.–351 с.