Часть 2. Случайные величины §1. Закон распределения случайной величины.

Случайное событие, которое проявляется в появлении некоторого числа, называется числовым случайным событием.

Полная группа числовых событий называется случайной величиной, а сами эти события - значениями случайной величины.

Случайной называют величину, которая в результате опыта принимает какое-нибудь значение, заранее неизвестно которое.

 Примеры.

• стрелок: количество попаданий в n выстрелах, возможные значения: 0,1,2,…,n

• бросание игральной кости: количество появлений 6-ти очков при n бросаниях, возможные значения: 0,1,2,…,n

• отклонение размера деталей, вырабатываемых станком, от эталона, возможные значения: любое число, которое не превышает по модулю допустимые припуски.

Случайную величину называют дискретной, если множество ее значений конечно или счетно. Дискретная случайная величина имеет такие возможные значения, которые расположенные на числовой прямой изолированно одно от другого.

Случайную величину называют непрерывной, если множество ее значений несчетно. Непрерывная случайная величина имеет такие возможные значения, которые заполняют числовую прямую или какую-то ее часть.

Законом распределения случайной величины называется любое соотношение, которое устанавливает связь между возможными значениями случайной величины и соответствующими вероятностями.

Случайные величины в целом помечают большими латинскими буквами, а конкретные возможные значения - соответствующими малыми. Например, запись означает, что величина X принимает конкретное значение , а запись означает вероятность для случайной величины X принять значение .

Распределение (закон распределения) дискретной случайной величины изображают в виде таблицы, в которой перечислены возможные значения случайной величины вместе с соответствующими вероятностями (синоним: ряд распределения):

			… …		… …
			… …		… …

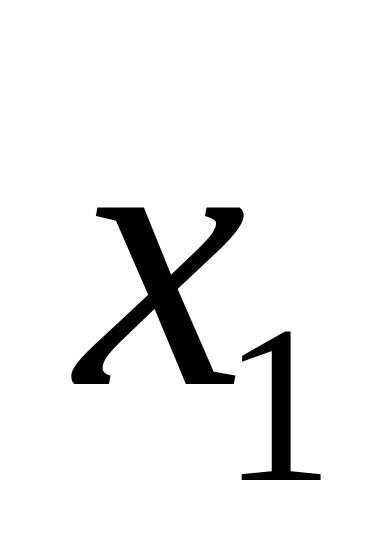
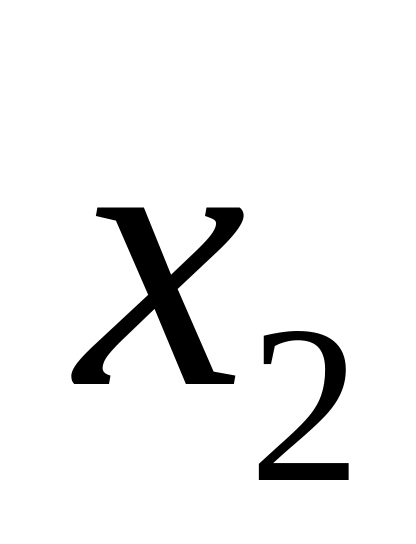
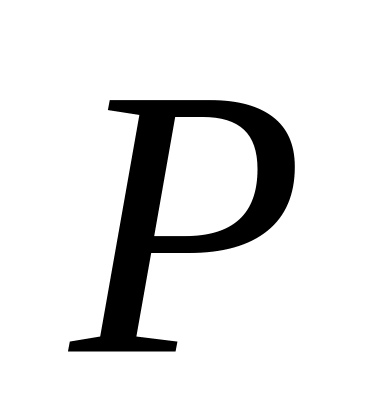
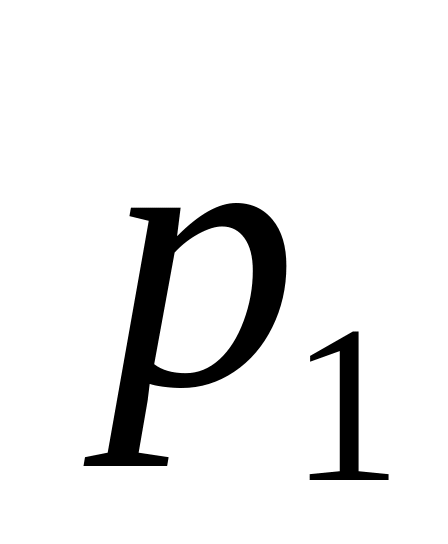
Причем, (по теореме о полной группе событий)

Для графического изображения закона распределения дискретной случайной величины используют многоугольник распределения. Он представляет собой построенные в прямоугольной системе координат точки (x_i, p_i), соединенные отрезками прямых.

Закон распределения для непрерывной случайной величины чаще всего представляют в функциональном виде, а графическое изображение - как график соответствующей функции.

§2. Функция распределения и плотность случайной величины

Функцией распределения случайной величины X называют функцию F(x), которая определяет для каждого значения x вероятность того, что случайная величина X примет значение меньше чем x:



• Функция распределения дискретной случайной величины

• Нередко в литературе F(x) называют интегральной функцией распределения.

Свойства функции распределения:

• 

• Функция распределения 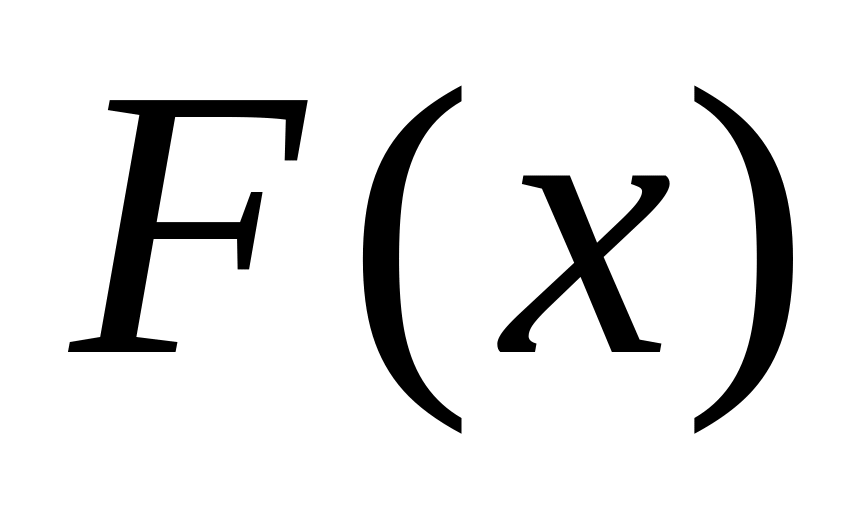- монотонно неубывающая,

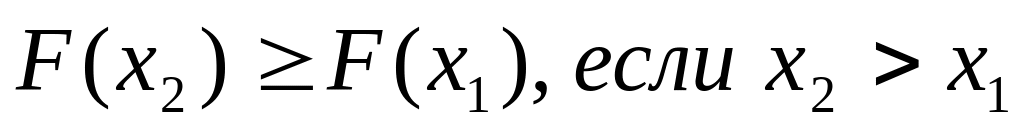
Следствие:

• Функция распределения - непрерывна слева

• 

• 

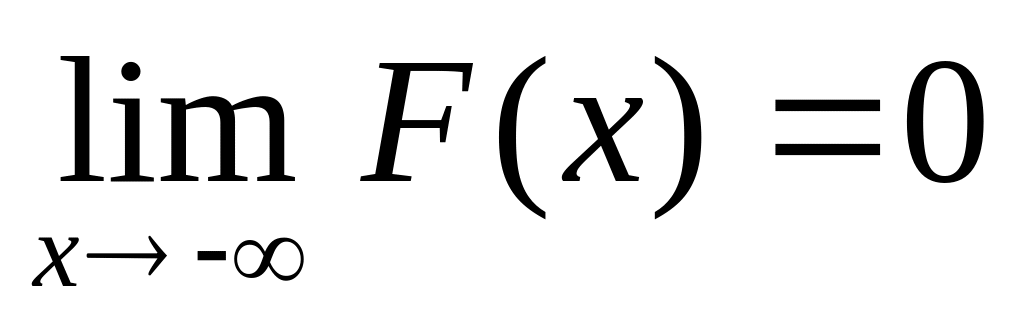
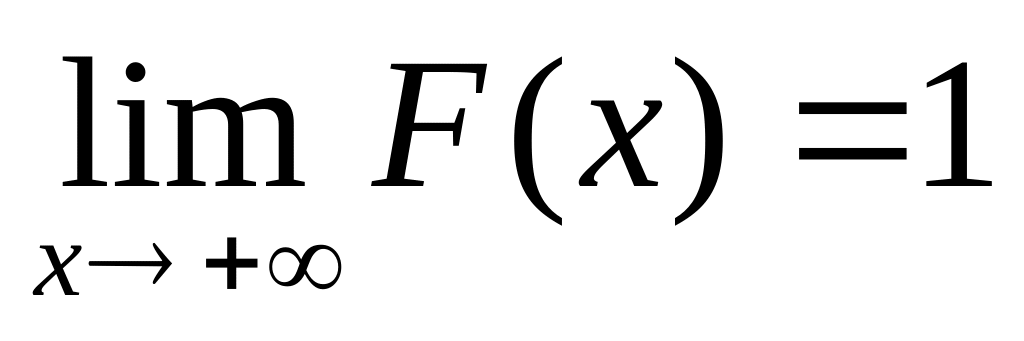
Плотностью распределения называют первую производную от функции распределения. Зачастую плотность распределения используют для определения непрерывных случайных величин.

Свойства функции плотности распределения:

• плотность распределения является неотрицательной функцией:

• 

• 

• 

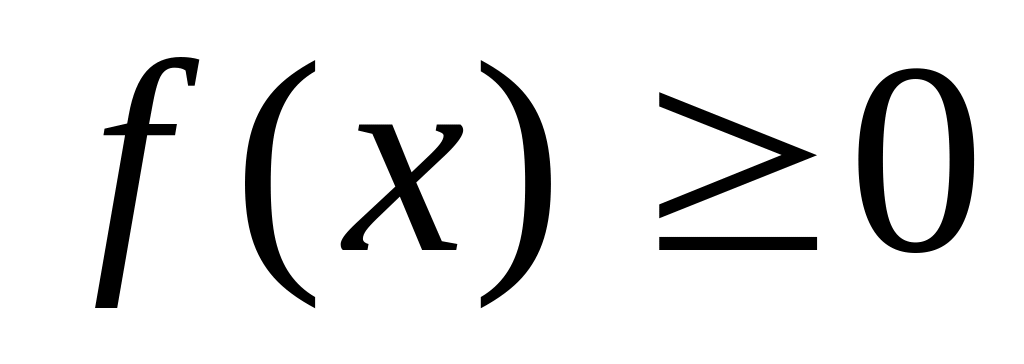
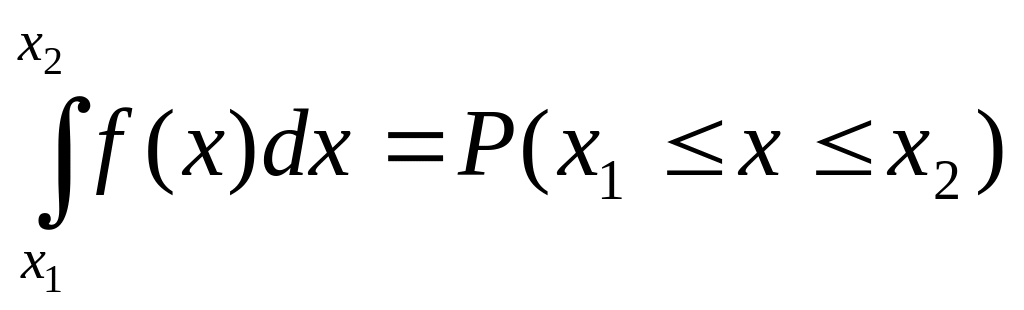
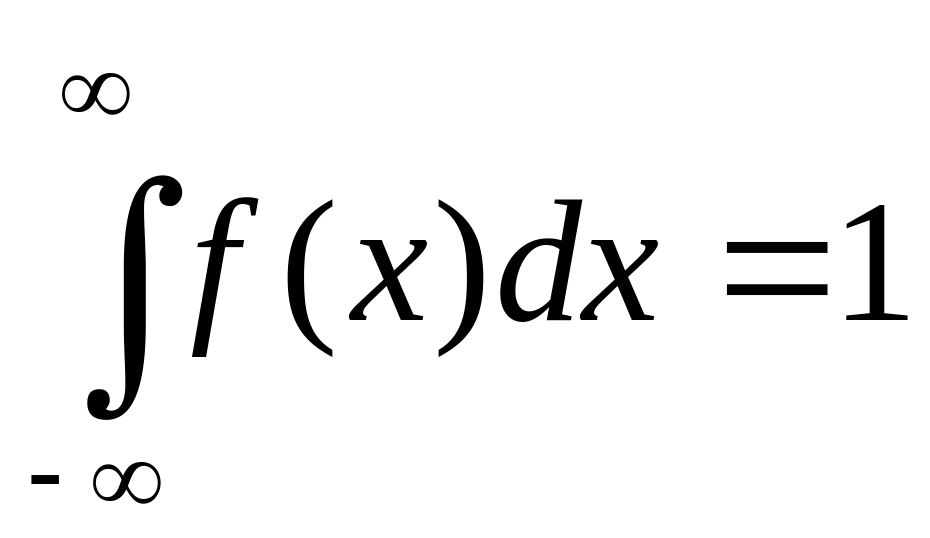
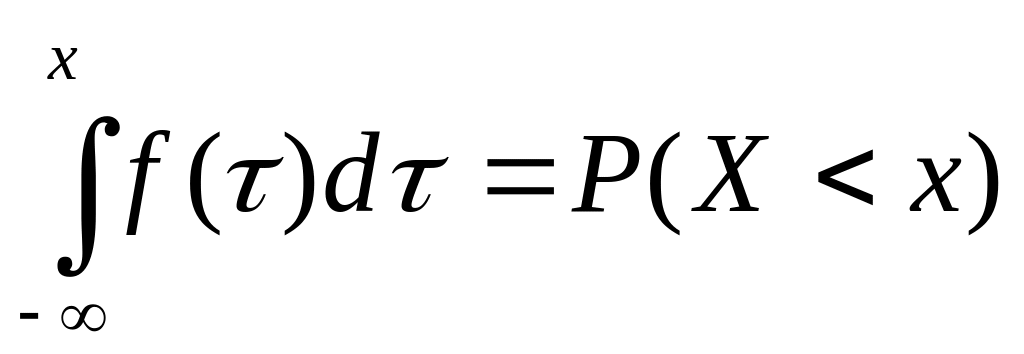
 Если случайная величина задана плотностью распределения, ее функцию распределения можно найти по формуле