М етоды расчета электрических цепей

1.5. Метод преобразования (свертывания) цепей

При наличии в цепи только одного источника ЭДС внешнюю по отношению к источнику, часть электрической цепи можно в большинстве случаев рассматривать как смешанное (последовательно-параллельное) соединение резистивных элементов. Расчет таких цепей проводят путем преобразования цепи до эквивалентного сопротивления. Определяют ток в ветви с источником ЭДС, а затем, используя закон Ома, рассчитывают токи в остальных ветвях.

ПРИМЕР (свертывание)

Дано:  В;  Ом;  Ом;  Ом; Ом;

 Ом.

Определить: , , , , .

Решение: Резисторы и соединены параллельно, их эквивалентное сопротивление  Ом

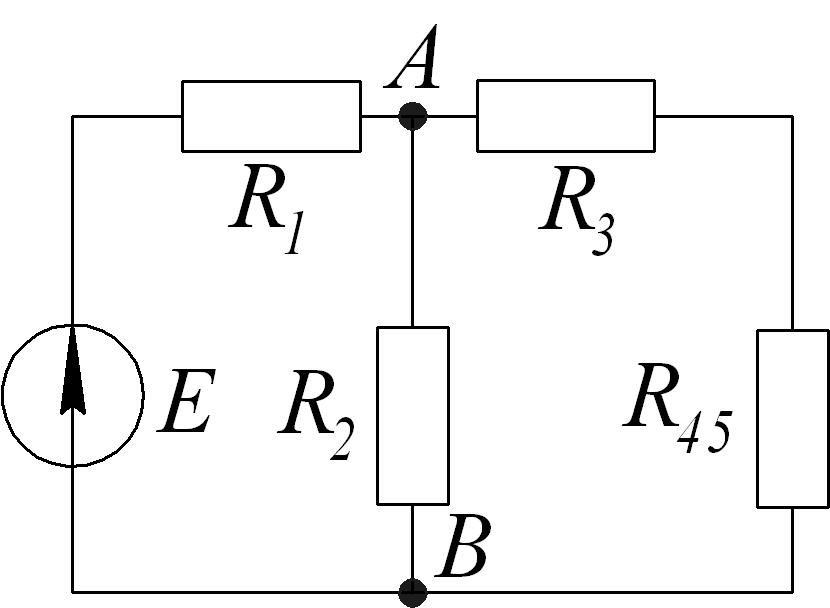
Резисторы и последовательны, находим их эквивалентное сопротивление  Ом.

и параллельны, их общее сопротивление  Ом.

Определяем ток :  А.

По закону Ома рассчитаем напряжение : , тогда  А.

Ток можно определить по I закону Кирхгофа:  А.

Для определения токов и найдем по закону Ома : , тогда  А;  А.

Напряжение можно не находить, подставив в формулы для нахождения и значения .

 А,  А.

1.6. Метод контурных токов

При расчете методом контурных токов полагают, что в каждом независимом контуре течет неизвестный контурный ток, а источники тока создают известные контурные токи. Относительно неизвестных контурных токов составляют систему уравнений вида:

где - контурные токи;

- собственные сопротивления контуров;

- сопротивления смежной ветви между контурами.

Сопротивление смежной ветви между «k» и «m» контурами ( ) входит в уравнение со знаком «+», если направления контурных токов и вдоль этой ветви одинаковы, и со знаком «-», если их направления противоположны.

- контурные ЭДС, равные алгебраической сумме ЭДС этого контура. В них со знаком «+» входят те ЭДС, направления которых совпадают с обходом контура.

Токи в ветвях находят как суперпозицию контурных токов.

Если схема содержит не только источники ЭДС, но и источники тока, то полагают, что ток источника тока замыкается по любым ветвям так, что вместе с ветвью источника создается замкнутый контур. Падение напряжения, вызванное током такого источника на каждом из сопротивлений контура, учитывается при записи левой части уравнений. Эти напряжения можно также учесть с обратным знаком в правой части уравнений.

1.7. Потенциальная диаграмма

Потенциальная диаграмма – это график распределения потенциалов вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с точки, потенциал которой принимают равным нулю, по оси ординат - потенциалы. Каждой точке рассматриваемого контура соответствует своя точка на потенциальной диаграмме.

ПРИМЕР 1.7.1.

Дано:  Ом;  Ом;  Ом;  Ом;  В;  В;  А;  А;  А.

Построить потенциальную диаграмму для контура авсdа.

Решение: Подсчитаем суммарное сопротивление контура авсdа  Ом и выберем масштабы по оси ординат. Точку а помещаем в начало координат. Определяем потенциалы в, с, d и их координаты.

Принимаем . Токораспределение в схеме при заземлении одной точки не изменится, т.к. никаких новых ветвей при этом не образуется.

 В, ;

 В, ;

 В, ;

 В, .