Катушка индуктивности с магнитопроводом в цепи синусоидального напряжения

Основным элементом конструкции различного рода электрических машин и аппаратов, устройств электроавтоматики, промышленной электроники, вычислительной техники является катушка индуктивности.

При наличие магнитопровода в катушке индуктивности (такая катушка называется дросселем) значительно возрастает магнитный поток, так как магнитная проницаемость ферромагнитного сердечника на несколько порядков больше магнитной проницаемости воздуха.

При подключении катушки с магнитопроводом к источнику синусоидального напряжения по обмотке катушки протекает переменный ток i, магнитодвижущая сила F = iw создает магнитное поле, индуктивность которого характеризуется магнитной индукцией B и магнитным потоком Ф.

В реальном дросселе большая часть магнитных линий замыкается по сердечнику (основной магнитный поток). Другая часть магнитных линий охватывает отдельные витки и группы витков обмотки, замыкается по воздуху и, частично, по магнитопроводу (поток рассеяния рис.4.19).

Рис.4.19. Катушка индуктивности с магнитопроводом.

Переменный магнитный поток индуктирует в обмотке ЭДС самоиндукции .

Если пренебречь сопротивлением обмотки и потоком рассеяния , то по второму закону Кирхгофа ЭДС самоиндукции уравновешивается величиной входного напряжения

или .

Из этого уравнения получаем закон изменения во времени магнитного потока:

или ,

т.е. при синусоидальном напряжении на входе катушки, магнитный поток в магнитопроводе также синусоидален.

Если величину амплитудного значения магнитного потока выразить через действующее значение напряжения и линейную частоту f, то

.

Поскольку действующие значения напряжения U и ЭДС самоиндукции E_L одинаковы, то

.

Данное соотношении применяют для расчетов ЭДС, индуктируемых в обмотках трансформаторов и называют уравнением трансформаторной ЭДС

Выясним, какова зависимость между током катушки индуктивности и магнитным потоком при синусоидальном питающем напряжении.

По заданной петле гистерезиса и зависимости построим кривую тока (рис.4.20).

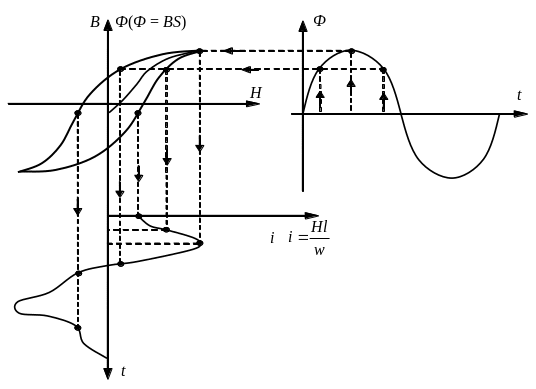
Рис.4.20. Форма кривой тока.

Из графика видно, что при синусоидальном потоке из-за нелинейности характеристики B(H), т.е. Ф(i) ток несинусоидален. Ток и магнитный поток достигают максимальных значений одновременно, но ток опережает магнитный поток по фазе на угол α.

Следовательно, при питании синусоидальным напряжением ток в катушке с ферромагнитным сердечником искажает свою форму и является несинусоидальным во времени.

Для упрощения расчетов несинусоидальный ток заменяют эквивалентным синусоидальным, имеющим одинаковое с несинусоидальным током действующее значение и развивающим одинаковую с ним активную мощность.

Схема замещения и векторная диаграмма реальной катушки с магнитопроводом

Обмотка реальной катушки с сердечником обладает активным сопротивлением R_обм. Магнитный поток является векторной суммой основного потока в магнитопроводе и потока рассеяния

.

Величина основного потока Ф определяется свойствами материала магнитопровода. Поток рассеяния Ф_σ зависит от конструкции обмотки, взаимного расположения витков, их сечения и составляет от основного потока. Потокосцепление рассеяния пропорционально току:

,

где L_рас – индуктивность рассеяния обмотки.

С учетом активного сопротивления обмотки и потокосцепления рассеяния напряжение на входе катушки

.

Таким образом, реальную катушку с магнитопроводом можно представить схемой замещения в виде последовательного соединения , и идеализированной катушки (рис.4.21). У идеализированной катушки обмотка не имеет сопротивления и рассеяния. Свойства идеализированной катушки зависят только от параметров магнитопровода и режима его намагничивания.

Рис.4.21. Схема замещения катушки индуктивности с сердечником.

Напряжение u₀ уравновешивает ЭДС индукции идеализированной катушки e_L и опережает магнитный поток на .

Переход к эквивалентным синусоидам тока дает возможность записывать все соотношения в комплексной форме и пользоваться векторными диаграммами.

Комплексное действующее значение входного напряжения запишется в виде

.

Схема замещения идеализированной катушки зависит от параметров магнитопровода и режима его намагничивания. Если предположить, что магнитопровод изготовлен из ферромагнетика с линейной зависимостью , то и выражение напряжения на входе катушки:

,

где - индуктивность идеализированной катушки.

Схема замещения реальной катушки для этого случая представлена на рис.4.20.а), соответствующая ей векторная диаграмма на рис.4.22.б).

Рис.4.22. Схема замещения реальной катушки индуктивности и реальная векторная диаграмма.

При учете потерь, обусловленных гистерезисом и вихревыми токами в сердечнике (зависимость B(H) петлевая), ток в обмотке катушки опережает магнитный поток на угол потерь α и может быть разложен на две составляющие.

Активная составляющая тока совпадает по фазе с напряжением U₀ и называется током потерь I_a = I_n, она определяется через мощность потерь в стали.

Реактивная составляющая тока отстает от напряжения U₀ на , называется током намагничивания I_p = I_μ и определяется из закона полного тока.

В комплексной форме ток .

Комплексное полное сопротивление идеализированной катушки:

.

Заменив идеализированную катушку последовательным соединением и получаем схему замещения реальной катушки для рассматриваемого случая (рис.4.23,а)

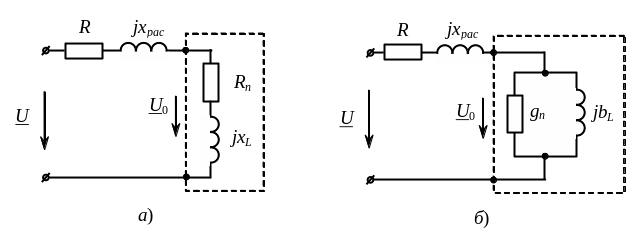
Рис.4.23. Последовательная и параллельная схема замещения нелинейной катушки индуктивности.

Переход от последовательной схемы замещения идеализированной катушки к параллельной (рис.4.23,б) проводится по формулам:

.

Векторная диаграмма реальной катушки индуктивности с магнитопроводом, имеющим петлевое намагничивание представлена на рис.4.24.

Рис.4.24. Векторная диаграмма реальной нелинейной катушки индуктивности.

При расчетах полное сопротивлении катушки индуктивности с магнитопроводом находят по закону Ома . Оно определяется главным образом индуктивным сопротивлением x_L = ω L (x_L >> R _обм).

Приближенно, пренебрегая активным сопротивлением обмотки и рассеянием магнитного потока, можно определить индуктивность L из соотношения или вычислить по потокосцеплению:

, где .

Эквивалентное активное сопротивление катушки определяется по значению активной мощности и току: