Тема анализ цепей постоянного тока с нелинейными резистивными элементами

Нелинейными электрическими элементами являются элементы, параметры которых зависят от тока и напряжения. Цепи, содержащие такие элементы, именуемые электрическими нелинейными цепями, обладают рядом новых свойств, которые отсутствуют у линейных цепей. Эти свойства позволяют создать основанные на них автоматические системы управления и регулирования, устройства для преобразования электромагнитной энергии, устройства для производства электрических измерений и передачи информации, быстродействующие вычислительные машины и т.д. Особенностью и сложностью анализа нелинейных систем является невозможность применения принципа наложения.

К нелинейным электрическим цепям постоянного тока относятся электрические цепи, содержащие нелинейные сопротивления, обладающие нелинейными вольт-амперными характеристиками, т.е. зависимость напряжения на зажимах резистивного нелинейного элемента от тока в нем задается его вольтамперной характеристикой (ВАХ).

Вольт-амперные характеристики могут быть заданы в виде графиков, таблиц и аналитических выражений.

Некоторые виды характеристик нелинейных элементов

В зависимости от вида характеристик различают следующие нелинейные элементы:

• с симметричной (относительно начала координат) и несимметричной характеристикой (рис. 10.1);

Рис. 10.1

• однозначные и многозначные (рис. 10.2);

Рис. 10.2

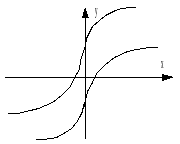
Рис. 10.3

• управляемыми - имеющие семейство характеристик, каждая из которых определяется управляющим элементом а; неуправляемыми - имеющие только одну характеристику (рис. 10.4).

Рис. 10.4

Статическими называют характеристики, в которых каждая точка дает значение постоянного напряжения при соответствующем значении постоянного тока. Из них определяют статическое сопротивление и статическую проводимость нелинейного элемента

.

Электрическое состояние нелинейных цепей постоянного тока описывается системой алгебраических уравнений, составленных по первому и второму закону Кирхгофа. Общих аналитических методов решения нелинейных уравнений не существует, поэтому решение таких задач осуществляется численными методами с использованием ЭВМ. Однако существуют наиболее простые методы расчета цепей постоянного тока с резистивными элементами - графические и графоаналитические: метод эквивалентных преобразований и метод пересечения характеристик.

Метод эквивалентных преобразований для нелинейных цепей, так же как и для линейных, основан на замене нескольких элементов одним и сводится к нахождению ВАХ эквивалентного нелинейного элемента.

При расчете электрических цепей с последовательным или параллельным включением нелинейных (или линейных и нелинейных) сопротивлений их вольт-амперные характеристики представляются в общей координатной системе и по ним строится общая вольт-амперная характеристика всей нелинейной электрической цепи.

а) При последовательном соединении нелинейных резистивных элементов, графически заданных своими вольт-амперными характеристиками, по оси абсцисс которых откладываются напряжения, а по оси ординат – ток, складываются абсциссы этих кривых для различных значений тока. Абсцисса каждой точки эквивалентного элемента при заданном токе находится как сумма соответствующих падений напряжения на сопротивлениях, поскольку при последовательном соединении по сопротивлениям протекает один и тот же ток цепи (рис.4.5.).

Рис.4.5. К расчету электрической цепи с последовательным соединением нелинейных элементов.

Таким образом, по общей вольт-амперной характеристике нелинейной цепи при заданном значении напряжения ЭДС легко определяют ток в нелинейной цепи I, а по заданному току, находят напряжение на каждом из последовательно соединенных сопротивлений, переходя к их вольт-амперным характеристикам.

б) При параллельном соединении нелинейных резистивных элементов складываются ординаты ВАХ для различных значений напряжения. Ордината каждой точки вольт-амперной характеристики эквивалентного нелинейного сопротивления при заданном напряжении определяют как сумму токов в ветвях соответствующего сопротивления , так как при параллельном соединении на всех сопротивлениях действует одно и то же напряжение (рис.4.6).

Рис.4.6. К расчету электрической цепи с параллельным соединением нелинейных элементов.

Следовательно, при параллельном включении сопротивлений, по общей ВАХ и заданном токе источника тока, нетрудно определить падение напряжения на параллельном участке цепи, а по известному напряжению, переходя к ВАХ каждого элемента, найти ток в каждом сопротивлении.

Применение графического метода расчёта цепей со смешанным соединением нелинейных резистивных элементов основано на методе свёртывания. Для получения характеристики всей цепи при смешанном соединении нелинейных элементов используются те же приемы, осуществляемые поочередно.

В методе пересечения характеристик реализуется графическое решение уравнения, определяющего электрическое состояние цепи при заданной величине источника.

а) При последовательном соединении линейного элемента и нелинейного резистивного элемента, графически заданного своей вольт-амперной характеристикой, решение задачи сводится к решению уравнения, составленного по второму закону Кирхгофа, и будет определяться точкой пересечения нагрузочной прямой с ВАХ нелинейного элемента. Для построения нагрузочной прямой, достаточно определить координаты двух точек, из опыта холостого хода и короткого замыкания. Напряжение холостого хода определяется по методу эквивалентного генератора. Точка пересечения линейной и нелинейной ВАХ получила название рабочей точки (рис.4.7.).

По второму закону Кирхгофа:

,

При , ;

при , .

Таким образом, из графика находятся ток в цепи и напряжение на нелинейном элементе, что представляют собой координаты точки пересечения.

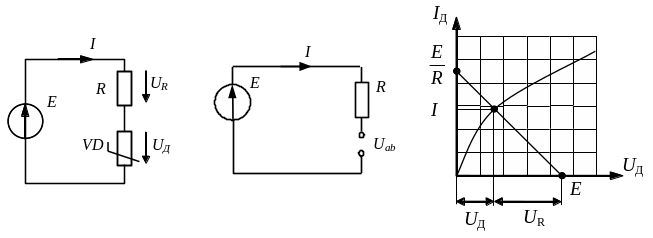
Р ис. 4.7 К расчету электрических цепей с последовательным включением нелинейного и линейного элементов методом пересечений.

б) При параллельном соединении линейного и нелинейного резистивного элемента, графически заданного своей вольт-амперной характеристикой, решение задачи сводится к решению уравнения, составленного по первому закону Кирхгофа, и будет определяться точкой пересечения нагрузочной прямой.

По первому закону Кирхгофа:

.

При , ;

При , .

Координаты точки пересечения двух ВАХ линейной и нелинейной являются найденным решением задачи. Они определяют ток в нелинейном элементе и напряжение на нелинейном и линейном сопротивлении (рис.4.8.).

Рис. 4.8 К расчету электрических цепей с параллельным включением нелинейного и линейного элементов методом пересечений.

Пример. Нелинейные сопротивления R₁ и R₂, включенные последовательно в электрическую цепь постоянного тока (рис.4.9 а), имеют вольт-амперные характеристики I и II, приведенные на рис.4.9, б. Определить ток I в цепи и напряжения U₁ и U₂ на этих сопротивлениях, если приложенное к цепи напряжение U = 60 В. В каких пределах измениться напряжение ΔU цепи при изменении тока I от I₁ = 25 мА до I₂ = 175 мА.

Решение. Строят общую вольт-амперную характеристику III указанных двух последовательно соединенных нелинейных элементов (рис.4.9, б) исходя из условия, что подводимое к цепи напряжение U при данном токе I нагрузки равно сумме напряжений на сопротивлениях R₁ и R₂, т.е. U=U₁+U₂.

Рис.4.9. К расчету электрических цепей с включением нелинейных элементов

Ток в цепи при напряжении U = 60 В согласно зависимости III определяется ординатой 0 – 5, соответствующей I₂ = 175 мА.

Напряжение на участках цепи находят из графических зависимостей. При токе I₂ = 175 мА, U₁ = 19 В (абсцисса 5-4), U₂ = 41 В (абсцисса 5-3). При токе I₁ = 25 мА напряжение, подводимое к цепи, U = 22 В. Следовательно, изменение подводимого к цепи напряжения при изменении тока в заданных пределах согласно рис. 4.9, б составляет: ΔU = 66 – 22 = 38 В.